由等高线重构曲面的HASMOC方法应用研究
2013-07-20宋敦江岳天祥
宋敦江,毕 诚,岳天祥
1.中国科学院 科技政策与管理科学研究所,北京 100190
2.中国兵器工业计算机应用技术研究所,北京 100089
3.中国科学院 地理科学与资源研究所,北京 100101
由等高线重构曲面的HASMOC方法应用研究
宋敦江1,毕 诚2,岳天祥3
1.中国科学院 科技政策与管理科学研究所,北京 100190
2.中国兵器工业计算机应用技术研究所,北京 100089
3.中国科学院 地理科学与资源研究所,北京 100101
1 引言
虽然新一代地球空间信息技术如InSAR、LiDAR和数字摄影测量等技术可快速获取DEM数据,但是传统的由人工解译地形得到的等高线仍然是一种十分重要的用于建立DEM的数据源[1]。广泛应用于科研与人们日常生活中的中国1∶25万、1∶5万及1∶1万DEM数据就是由等高线和离散点通过约束TIN(Triangulated Irregular Networks)方法构建得到[2-3]。等高线是从摄影测量立体相对模型中通过人工判断提取获得,是人对地形地貌(Landforms)抽象理解和概括而获得的一种数据,它蕴含着大量的地形特征信息[3]。等高线表示地形时有很多类似TIN模型之处,如在地形变化平缓的地方等高线稀疏,在地形变化急促的地方等高线密集。为了充分利用等高线蕴涵的大量地形特征信息,在建立DEM时应选择针对等高线的方法,而不是选择通用的空间插值方法,如样条法(Spline)、反距离权重(IDW)及克里金(Kriging)方法。早在1728年人们就开始应用等高线[4],近20多年来,国内外对于等高线构建DEM方法的研究却一直没间断过,由等高线建立地形曲面的方法主要有TIN方法[5]、薄板样条法(Thin Plate Spline,TPS)[6]、等高线膨胀法(Contour Dilation)[7]、最大中间等高线法(Max Intermediate Contours,MIC)[8]、最陡坡度法[9]和地形骨架线法(Skeleton)[10]及综合方法(综合使用中间等高线、最陡方向及地形骨架线等方法)[11]。这些方法各有优劣,如TIN方法在谷地和山峰生成“平三角”,两等高线间利用线性插值,与实际地形的连续过渡的现象不符;最陡坡度法考虑到两条等高线之间的线性关系,而实际上两条等高线之间的最陡方向线常常难以求得,这使得最陡坡法成为一个思想方法,而不是一个具体的算法,限于篇幅,其他方法不一一论述。
HASM(High Accuracy Surface Modeling)是我国学者21世纪初提出的基于微分几何曲面论的曲面建模新方法[12]。曲面论的基本思想是,一个曲面除了它的空间位置外,它的形状由它的第一类基本式和第二类基本式决定[13]。HASM通过迭代计算获得曲面的两类基本式系数,从而模拟得到一个曲面的形状。HASM方法目前主要用于由离散点模拟曲面的研究。HASMOC方法也被称为基于曲面论和优化控制理论的曲面建模方法,它是在HASM方法基础上的扩展,增加了更多的约束条件,目前主要用于由等高线(也可以包含离散点)重构地形曲面[14-15]。HASMOC方法的应用最早发表于2010年的科学计算与优化国际会议[16],当时用于数学曲面的等高线重构曲面的研究,得到较理想的结果,详细结果可参见《Surface Modeling:High Accuracy and High Speed Methods》第7章,2011年HASMOC方法申请了国家专利,比较了HASMOC方法与薄板样条的模拟结果的区别[17],但是以上相关文献中仍然缺少本文的很多细节的描述,特别是对于不同方法的模拟结果DEM高程频率分布特性的统计比较、回放等高线的细节分析。
多条等高线形成的“等高线群”能较好地概括和表现地形地貌特征,等高线既蕴含着定量的信息,如等高线所经过位置点的高程信息;还蕴含着定性信息,如两条等高线间的网格点的高程上下界,等高线还蕴含着山峰、山谷和鞍部以及山脊线、沟谷线等定性信息[1]。等高线树是用于表示等高线空间拓扑关系的一种数据结构,等高线拓扑关系主要包括父子包含关系,以及兄弟并列关系。等高线树的研究方兴未艾,自1963年“等高线树”这一概念出现以后[18],涌现了很多构建等高线树的方法[19]。通过等高线树,可以快速地计算出研究区域内任意一点与等高线的空间关系,如该点被哪条等高线包含,不被哪条等高线包含,从而获得区域内任意一个格网点高程的上下界(为包围该格网点的所有等高线高程的最小值与最大值,开区间)。
本文分别应用HASMOC方法和TIN方法根据等高线重构地形曲面,比较分析了这两种方法得到的重构曲面的一些特性,包括曲面的光滑性、回放的等高线、高程值的分布频率等。由于TIN方法的介绍说明非常常见,这里不再赘述。
2 HASMOC方法
设{(xi,yj)|xi=i×h,yj=j×h,0≤i≤I+1,0≤j≤J+1}是计算区域Ω进行均匀正交剖分的网格,其中h为网格分辨率,则HASM主方程Dirichlet边界问题的有限差分迭代形式可表达为:

表示迭代过程中网格点(x,y)上第n次迭代的模拟ij值,等变量的具体含义,可参见文献[12]。
设

以上两个方程可以用矩阵形式表达为:

其中,A和bn分别为方程组(1)中第1个方程的系数矩阵和右端项向量;B和cn分别为方程组(1)中第2个方程的系数矩阵和右端项向量。设:

则HASM方法可以表示为如下等式约束最小二乘问题:

其中S∈RT×(I×J)和t∈RT×1分别为采样矩阵(布尔矩阵)和采样向量,T为采样点个数。建立等式约束最小二乘方法的目的是为了在保证采样点处模拟值接近采样值的条件下,曲面的整体模拟误差最小。
等高线(结合图廓边界),将研究区域分割成多个子区域。对于每个子区域内的格网点,根据包围它的等高线,可以确定格网点高程值的范围。如图1所示,方格代表一个栅格单元,中间的点表示该栅格的中心点,标注的数字21~88表示格网点编号,等高线间距为2.5 m,等高线的高程值用红色数字标注。
对于每个网格点,可以根据其所在的子区域,获得其高程范围。l、u分别表示网格点高程值上下界的列向量,f表示待求的模拟变量。网格点51被等高值为117.5和120的等高线所包围,对网格点51的高程,应该满足不等式l(51)<f(51)<u(51),其中l(51)=117.5和u(51)=120。网格点46,被一条高程为132.5的山顶等高线包围,同时其附近还存在一个采样点(高程为134),这种情况,可以近似认为,这个采样点是山峰点,故可得不等式l(46)<f(46)<u(46),其中l(46)=132.5,u(46)=134。若网格点46所在的这个山峰没有采样点,则其高程所满足的不等式中,上界值u(46)为135,即为围成这片区域等高线的等高值加上1倍的等高距。对于洼地区域,可做类似处理。

图1 根据等高线确定离散格网点上下界约束示意图
对于每个网格点,其高程都可以建立不等式方程,从而得到不等式组,故曲面应该一直满足不等式约束优化模型:

方程(5)即为HASMOC方法,它可以使用Matlab 7.8的lsqlin函数进行求解。lsqlin主要用于解决不等式约束的最小二乘的曲线拟合问题:

x=lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0,οptiοns),这里的C是一个m×n的稀疏矩阵,它是方程组(1)的矩阵系数,lb和ub表示的从等高线中求得的变量的上下界,x0是待求量的初始值,οptiοns是关于优化求解参数的选项,本文的约束优化求解的参数皆为默认参数,初始值为元素全部为0的列向量。
3 应用案例
中国科学院千烟洲生态试验站位于江西省中部,隶属于吉安市泰和县,处于115°04′13″E,26°44′48″N,是一个由约80个小山丘,9条沟谷组成的小山村,总面积约为2.04 km2,海拔高程60~150 m左右,属典型的红壤丘陵区。地貌类型主要是低丘,丘顶浑圆,海拔多在100 m以下,最高达147 m,相对高度20~50 m,丘坡坡度以10°~30°居多。本实验数据是在江西省吉安市泰和县纸质地形图的基础上,针对千烟洲生态试验站附近的地形图扫描然后人工矢量化得到的数据,1954年北京坐标系,1956年黄海高程系,等高距2.5 m,199?年(原图看不清),该区域内多植被,且大部分为水稻田。为验证HASMOC方法在稀疏等高线情况下的有效性,从2.5 m等高距的等高线中抽取了20 m等高距的等高线(见图2)(共计76条等高线)进行重构地形曲面的实验。
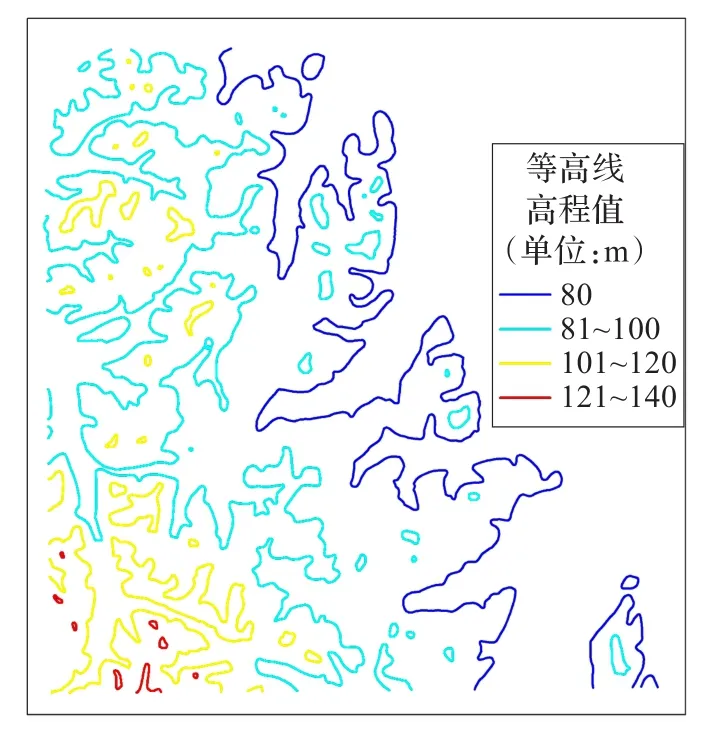
图2 千烟洲扫描矢量化原始等高线数据(20 m等高距)
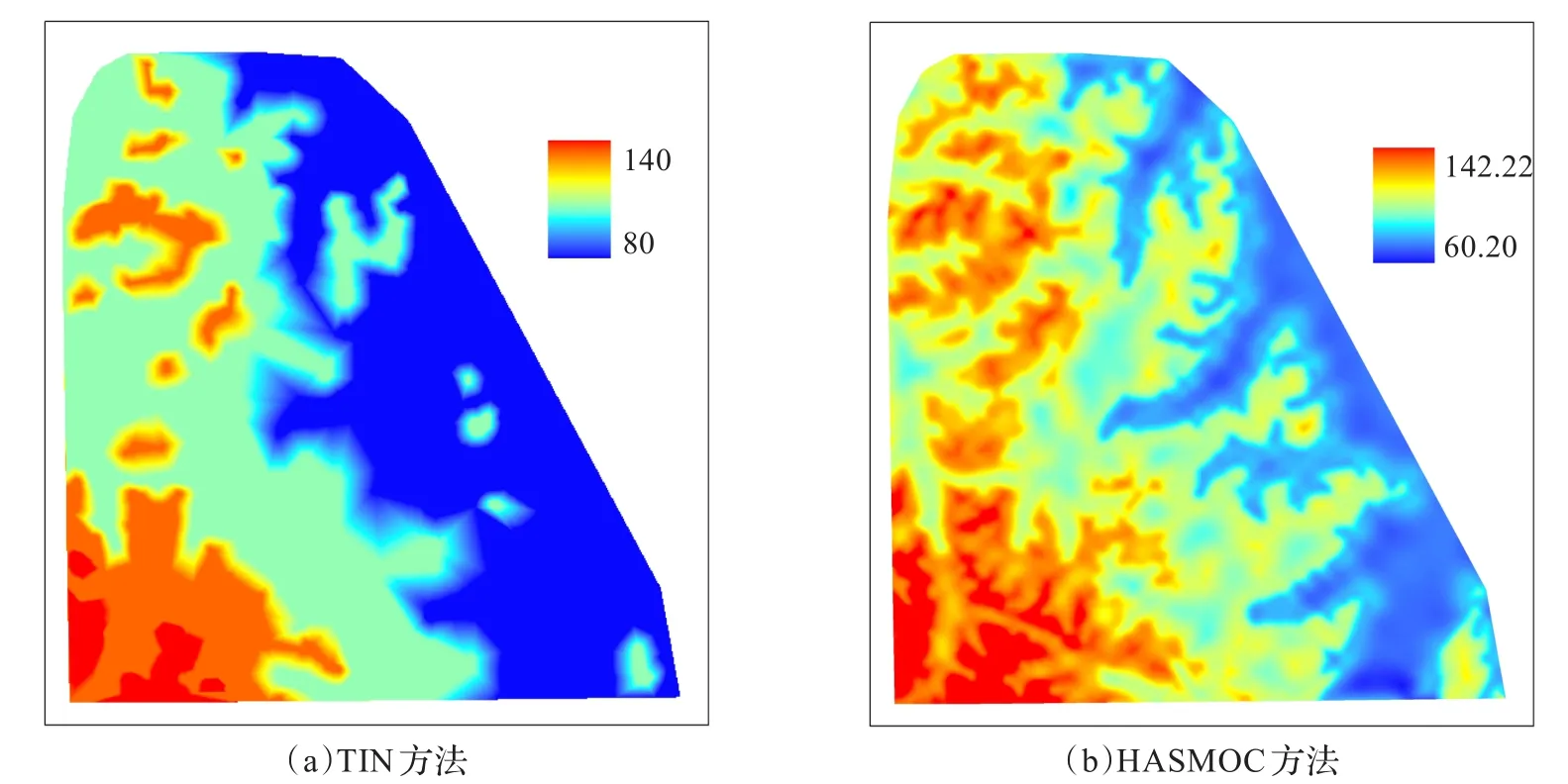
图3 DEM结果比较图(高程单位:m)
利用图2中的等高线数据,分别使用TIN和HASMOC方法建立5 m分辨率DEM(图3),TIN方法模拟得到的结果为等高线的凸包,HASMOC模拟方法返回的是外接矩形区域(521行×546列),为了统一起见,只显示了与TIN相同范围的DEM。从图4中可以看出,TIN在地形中的山顶和谷地出现了很多“磨平”现象,遗弃了很多地形细节,而HASMOC方法则基本保留了地形细节,地形曲面连续光滑、自然。在多处“弯月”型山谷中,TIN方法构建的DEM严重失真,未保证建立的DEM忠实于原始等高线;在多个马鞍处,TIN方法也出现磨平现象。通过回放等高线(图4)可看出,TIN方法回放的等高线(共计35条)与原始等高线的相差非常大,而HASMOC方法回放的等高线与原始等高线的形状基本一致(都是76条等高线)。类似地,还进行了从2.5 m等高距的等高线中抽取了10 m等高距实验,得到类似的结果,TIN方法回放的等高线(110条)与原始等高线(152条)相差非常大,而HASMOC方法则与原始等高线基本吻合,等高线的条数相等。

图4 回放等高线(蓝色+横条)与原始等高线(黑色)叠加分析图
理论上,通过对等高线间各子区域的约束优化控制,HASMOC方法能保证回放等高线的最大偏离距离不超过一个栅格单元,这点可以通过图5得到佐证。图5中的数字编号是等高线的标识号,等高线69的回放等高线与原始等高线的差别较大,但是两条等高线的最大距离没有超过一个栅格单元宽度。等高线53也存在3处相差较大的情况,但是都没有超过理论上的最大距离。

图5 HASMOC方法回放等高线局部放大图
根据文献[20]的研究,由等高线建立的DEM容易受到等高线数据本身的影响,如DEM中等高线高程值附近的栅格单元数相对较多,这是DEM构建方法无法避免的,这与实际地形严重不符,于是DEM的高程频率分布柱状图也是检验构建DEM方法优劣的一个标准。从图6中可以看出,TIN方法构建的DEM受原始等高线数据的影响很大,分别在高程值为80、100和120处的高程点分布较多,HASMOC方法模拟结果也受到了一定的影响,但是相对来说影响很小。
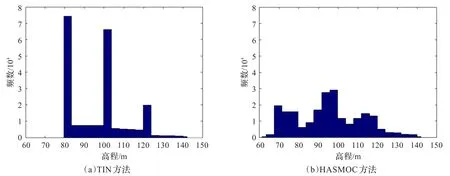
图6 高程频率统计柱状图
4 结束语
HASMOC方法较TIN方法模拟得到了更加符合实际的DEM:(1)从DEM结果来看,TIN产生大量的磨平现象,丢失了很多地形细节,HASMOC保留了大量的地形细节;(2)HASMOC回放等高线与原始等高线基本吻合,TIN的回放等高线与原始等高线差别很大;(3)TIN方法构建的DEM高程值分布频率受等高线数据影响大,HASMOC受到的影响小。
由等高线(或等值线)重构曲面方法在机械锻造等工业加工过程中应用广泛,HASMOC方法采用曲面离散化方法,最后的求解过程计算量大,本文运用Matlab中的lsqlin函数进行求解,可能速度上无法满足实际企业生产的实时需求,运算速度有待提高。运用GPU并行计算技术实现大规模优化控制问题的快速求解,是下一步的研究工作。
[1]Gallant C,Hutchinson M F.Digital elevation models and representation of terrain shape[M]//Terrain Analysis:Principles and Applications.[S.l.]:John Wiley and Sons,2000.
[2]Li Zhilin,Zhu Qing,Gold C.Digital terrain modeling:principles and methodology[M].[S.l.]:Taylor&Francis,2005.
[3]El-Sheimy N,Valeo C.Digital terrain modelling:acquisition,manipulation and applications[M].Norwood:Artech House,Inc,2005.
[4]Cayley A.On contour and slope lines[J].Philosoph Mag,1859,18:264-268.
[5]Garcia,Bello A.A contour line based triangulating algorithm[C]// Bresnahan P,Corwin E,Cowen D.Proceedings of the 5th International Symposium on Spatial Data Handling,1992:411-423.
[6]Hutchinson,Michael.Calculation of hydrologically sound digital elevation models[C]//Proceedings of the Third International Symposium on Spatial Data Handling.Columbus,Ohio:International Geographical Union,1988.
[7]Taud H,Jean-Francois P,Alvarez R.DEM generation by contour line dilation[J].Computers&Geosciences,1999,25(7):775-783.
[8]Gousie M B,Franklin W R.Constructing a DEM from gridbased data by computing intermediate contours[C]//GIS 2003:Proceedings of the Eleventh ACM International Symposium on Advances in Geographic Information Systems,2003:71-77.
[9]Ardiansyah P O D,Yokoyama R.DEM generation method from contour lines based on the steepest slope segment chain and a monotone interpolation function[J].ISPRS Journal of Photogrammetry and Remote Sensing,2002,57(1/2):86-101.
[10]Thibault D,Gold C M.Terrain reconstruction from contours by skeleton construction[J].GeoInformatica,2000,4:349-373.
[11]胡鹏.新数字高程模型[M].北京:测绘出版社,2007.
[12]Yue Tianxiang,Du Zhengping,Song Dunjiang.A new method of surface modeling and its application to DEM construction[J].Geomorphology,2007,91(12):161-172.
[13]Ciarlet P G,Larsonneur F.On the recovery of a surface with prescribed first and second fundamental forms[J].J Math Pures Appl,2002,81:167-185.
[14]Yue Tianxiang,Song Dunjiang,Du Zhengping.Chapter 7“An optimal control method of HASM for DEM construction and its validation”[M]//Surface Modeling:High Accuracy and High Speed Methods.[S.l.]:CRC Press,2011.
[15]岳天祥,杜正平,宋敦江.基于曲面论和优化控制理论的曲面建模方法:中国,201110021504.8[P].2011-05-11.
[16]Song Dunjiang,Yue Tianxiang,Du Zhengping.DEM construction from contour lines based on regional optimum control[C]// Proceedings of the Third International Joint Conference on Computational Sciences and Optimization,2010:162-165.
[17]宋敦江,岳天祥,杜正平.一种由等高线构建DEM的新方法[J].武汉大学学报:信息科学版,2012,37(4):472-476.
[18]Boyell R,Reston H.Hybrid techniques for real-time radar simulation[C]//Proceedings of the Fall Joint Computer Conference,Las Vegas,1963:445-458.
[19]Chen Jun,Qiao Chaofe,Zhao Renliang.A voronoi interior adjacency-based approach for generating a contour tree[J]. Computers&Geosciences,2004,30:355-367.
[20]Carla R,Carrara A,Bitelli G.Comparison of techniques for generating digital terrain models from contour lines[J].International Journal of Geographic Information Science,1997,11(5):451-473.
SONG Dunjiang1,BI Cheng2,YUE Tianxiang3
1.Institute of Policy and Management,Chinese Academy of Sciences,Beijing 100190,China
2.Computer Application Technology Institute of China North Industries Group Corporation,Beijing 100089,China
3.Institute of Geographical Sciences and Natural Resources Research,Chinese Academy of Sciences,Beijing 100101,China
The HASMOC(High Accuracy Surface Modeling-Optimal Control)method is based on HASM,on which more constraint equations are added.The latter is mainly used to reconstruct surface from discrete points,while the former can be also used to reconstruct terrain surface from contours.By minimizing the norm of the combining equation of the two basic equations of the HASM method,subject to the equality constraints from sample points and bound constraints for each grid points which are surrounded by contours,HASMOC method can preserve the smoothness of the terrain surface,and the high fidelity to the original contours.A real contour lines example is given,and results from HASMOC are compared with that from TIN(Triangulated Irregular Network)method,as for the respects of retrieved contour,details of surface and histogram of surface height distribution,the former is superior to the latter in terrain surface reconstruction from real contour lines.
High Accuracy Surface Modeling(HASM);optimal control;Triangulated Irregular Network(TIN);retrieved contours;histogram of height distribution
HASM优化控制方法(High Accuracy Surface Modeling-Optimal Control,HASMOC)是在高精度曲面建模(HASM)方法的基础上,增加更多约束条件方程后形成的一种方法。通过对等高线间格网点高程范围的约束优化控制,最小化HASM基本方程的模,HASMOC方法既能保证地形曲面的整体光滑性,又保证地形曲面对于原始等高线数据的忠实性。实际案例表明,HASMOC方法得到的地形曲面结果优于TIN方法的地形曲面模拟结果;比较分析地形曲面的回放等高线、地形光滑程度和地形曲面的高程分布频率等,可以看出,HASMOC方法能较好地克服TIN的缺点。
高精度曲面建模(HASM);优化控制;不规则三角网(TIN);回放等高线;高程分布频率
A
TP391
10.3778/j.issn.1002-8331.1304-0349
SONG Dunjiang,BI Cheng,YUE Tianxiang.Application of HASMOC method in terrain surface reconstruction from contours.Computer Engineering and Applications,2013,49(18):171-175.
中科院135创新项目(No.Y201131Z06);国家自然科学基金青年科学基金(No.40801187);国家自然科学基金杰出青年科学基金(No.40825003)。
宋敦江(1979—),男,博士,副研究员,研究领域为计算管理学;毕诚(1975—),男,高级工程师,研究领域为机电一体化与可视化;岳天祥(1963—),男,博士,研究员,研究领域为资源环境模型与系统模拟。E-mail:songdj@casipm.ac.cn
2013-04-24
2013-07-23
1002-8331(2013)18-0171-05
