各向异性扩散图像去噪的改进模型

郑满满，胡小兵，郑申海

重庆大学 数学与统计学院，重庆 401331

各向异性扩散图像去噪的改进模型

郑满满，胡小兵，郑申海

重庆大学 数学与统计学院，重庆 401331

1 引言

图像去噪是图像处理中非常重要的部分，图像去噪的目的就是尽可能地减少图像的噪声，同时尽可能多地保留图像原有信息。传统的图像去噪方法有很多，如高斯滤波、中值滤波、均值滤波等，但是传统滤波容易在噪声平滑过程中丢失掉边缘。基于PDE的图像平滑技术为解决这一矛盾提供了新方法[1-5]。

20世纪90年代初，Perona和Malik[1]提出用具有方向性（异性）的热扩散方程来代替高斯平滑滤波器，这种方法不仅减弱了模糊程度，还抑制了噪声。但是P-M模型存在一些缺陷[3-4]。1992年，Cattle，Lions，Morel和Coll[5]对P-M模型作出了改进，提出了选择平滑C模型，解决了P-M模型存在的某些问题，在理论上证明该模型满足解的适定性。然而，许多实验表明C模型仍存在一些问题[3-5]，该模型的保边缘效果仍有待改进且当参数σ趋于0时，该模型不稳定。对此，许多学者试图对P-M、C模型进行改进，并取得了一些进展[6-9]。

本文在分析各向异性扩散方程中扩散系数行为的基础上，改进了C模型中的扩散系数。由于仅靠梯度不能很好地区分边缘点，故改进模型在扩散系数函数中引入二阶导数uxx、uyy，利用二阶导数锐化边缘[10-11]；此外，改进模型针对不同的梯度范围采取程度不同的扩散行为，这样不仅能够有效地保护边缘，而且还能够避免小尺度噪声敏感及细节失真的问题。

2 传统各向异性扩散模型

2.1 P-M模型

Perona和Malik在1987年指出高斯滤波不能保护图像的自然边缘，不同的尺度下图像的边缘在移动。为了去噪同时保护边缘，得到如下扩散模型：设原始图像u(x，y，0)=u(x，y)，随时间t的演化图像u(x，y，t)，演化规则为：

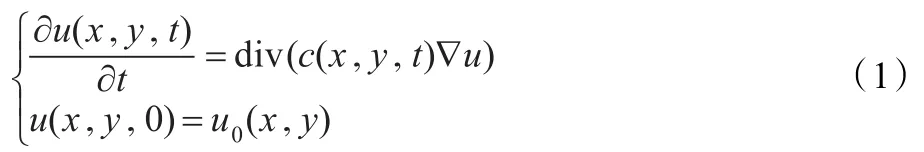
其中，c(x，y，t)为扩散系数。当c(x，y，t)=1时，退化为热传导方程。此时的扩散就是各向同性的。c(x，y，t)是关于梯度的函数，理论上，希望在非边缘区域c(x，y，t)尽量大，图像充分平滑；在边缘附近c(x，y，t)≈0，图像不再平滑。通常取：

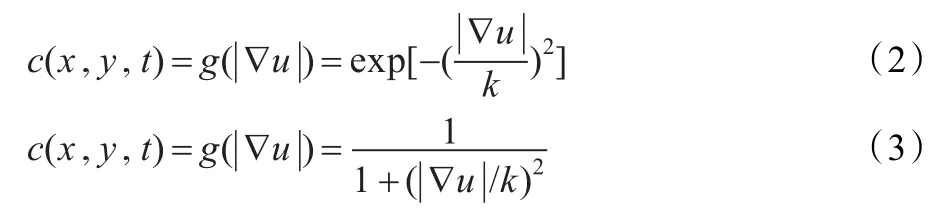
P-M模型存在着以下的缺陷和局限性：

（1）在噪声处，图像的梯度可能非常大，此时平滑系数较小，噪声点被保留下来；

（2）P-M是病态模型，不稳定。

2.2 C模型

针对P-M模型的不足，C模型的解决办法是先对噪声图像进行高斯平滑，降低噪声点的梯度，再运用P-M模型滤波，就会得到较好的效果。Cattle，Lions，Morel和Coll提出的C模型如下：其中Gσ*∇u表示热传导方程在σ时刻的梯度。用|Gσ*∇u|代替| ∇u|克服了P-M模型对噪声敏感的不足，且C模型的解存在唯一。C模型存在着以下的缺陷和局限性：

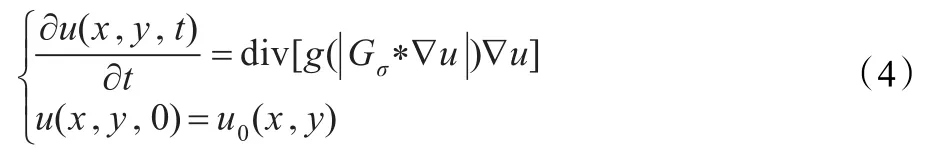
（1）该模型仅用梯度来识别边缘，不够准确，保边缘效果仍然有改进空间；

（2）当参数σ趋于0时，该模型不稳定。

3 各向异性扩散改进模型

在上面分析的基础上，提出一种改进的各向异性扩散模型。改进模型将扩散系数函数中加入二阶偏导数uxx，uyy，使扩散速度由梯度信息和二阶导数共同决定，这样能较好地识别图像边缘防止被平滑。另外一方面，改进模型是基于梯度阈值的有选择地进行图像平滑[12-14]，根据|Gσ*∇u|的大小来选择不同程度的扩散系数，使得模型在连续的尺度区域内得到较好的平滑效果。改进的扩散系数表达方式：

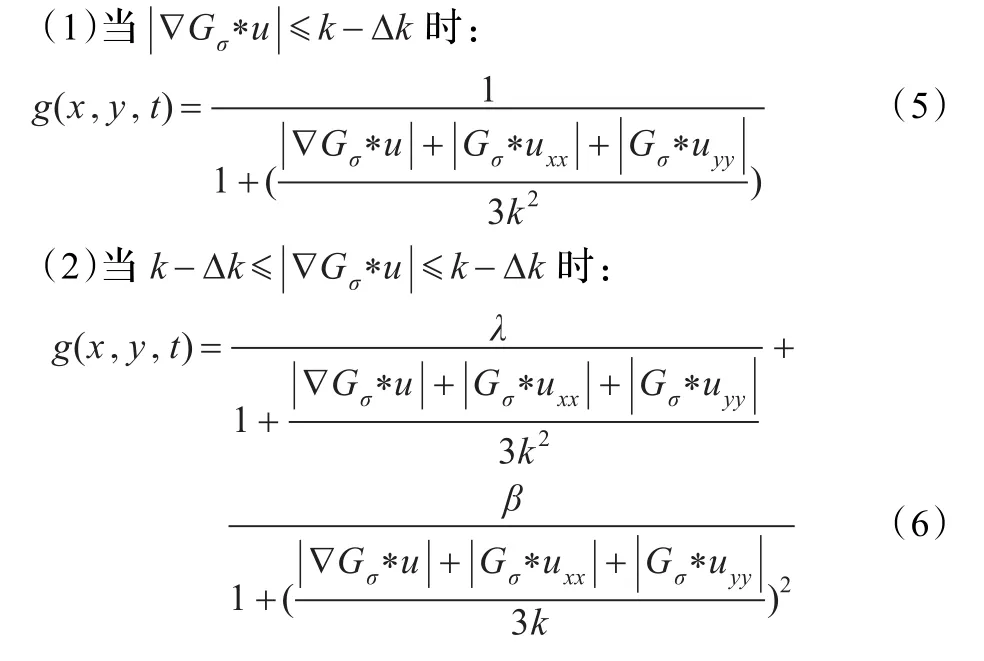
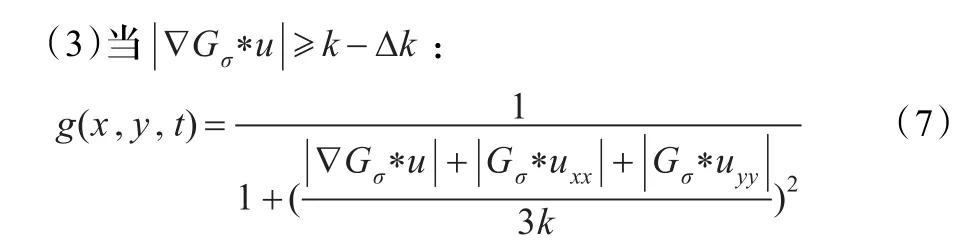
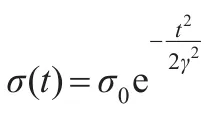
4 数值实现

把改进的扩散系数应用到C-模型中，得到：

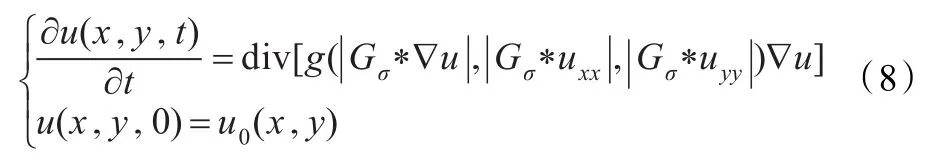
这里采用有限差分对改进模型离散[1，15]。变量x、变量y上取等距离离散空间步长h，时间步长为Dt。化简方程得到如下形式：

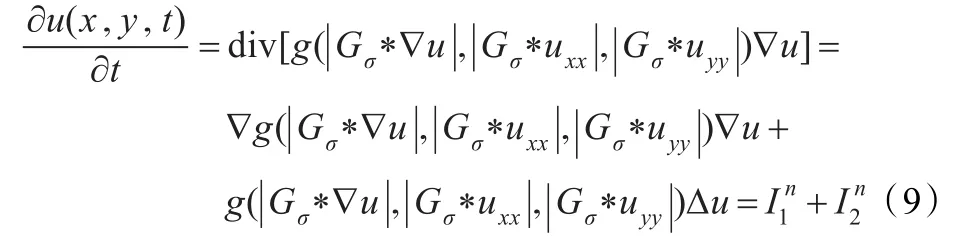
其中第一项差分格式为：

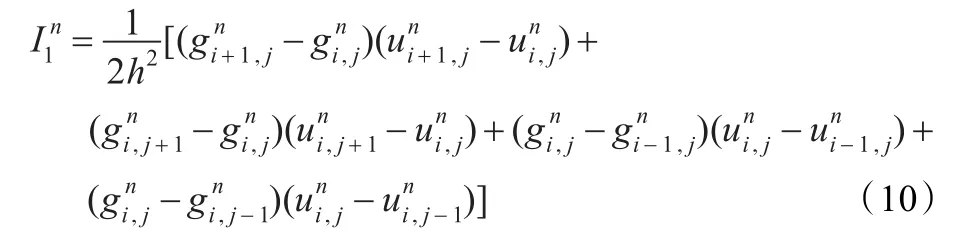
其中第二项差分格式为：

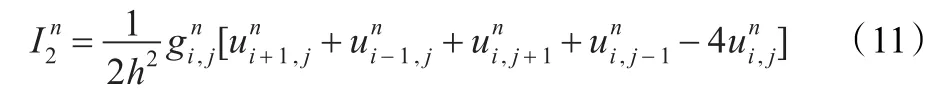
5 基于相关系数的图像去噪质量评判标准

应用相关系数这一函数作为评判图像去噪质量的准则[16]。理论指出当噪声与图像的信号无关时，可用相关系数来评定图像去噪的效果。考虑去噪后的图像与添加噪声前的图像的相关系数，如果这两幅图像的相关性越强则说明图像去噪的效果越好。即当两幅图像相关系数取最大值时，图像去噪效果最佳。另外可选择相关系数最大值时的时间点为迭代停止的最佳时间。用函数表示：

其中f表示添加噪声前的原始图像，u表示去噪后的图像。式（12）表示求两幅图像相关系数的极大值。

6 实验结果与分析

6.1 实验结果

实验结果如图1～8所示。

图1 噪声方差0.01去噪效果

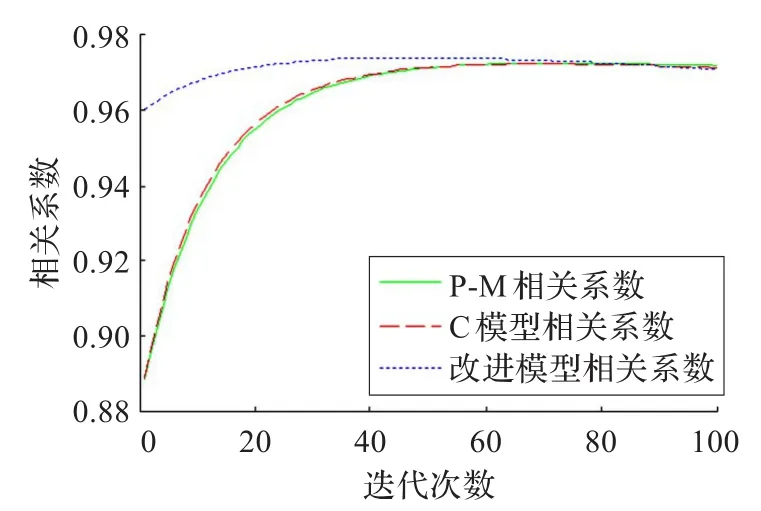
图2 噪声方差0.01的相关系数

图3 噪声方差0.02去噪效果

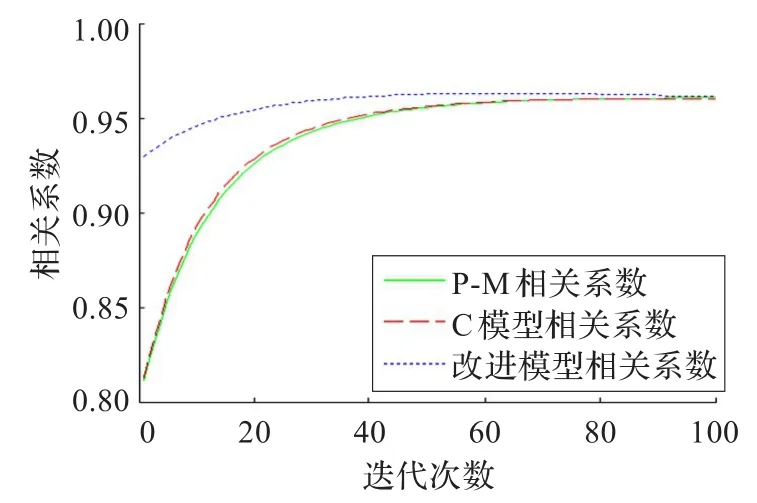
图4 噪声方差0.02相关系数

6.2 实验结果比较

实验结果比较如表1、表2所示。

图5 噪声方差0.03去噪效果

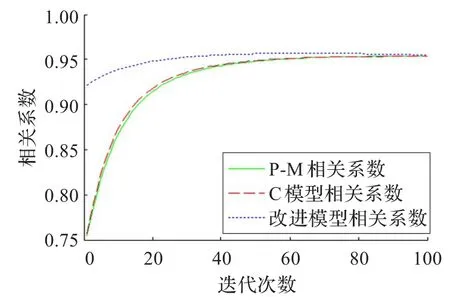
图6 噪声方差0.03相关系数

图7 噪声方差0.04去噪效果

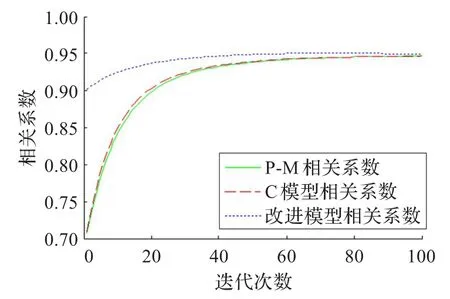
图8 噪声方差0.04相关系数

6.3 实验结果分析

（1）从视觉效果观察lenna的去噪图像可看出，在迭代次数相同前提下，P-M模型、C模型的效果都不如改进模型。

表1 噪声方差不同时各模型的最大相关系数

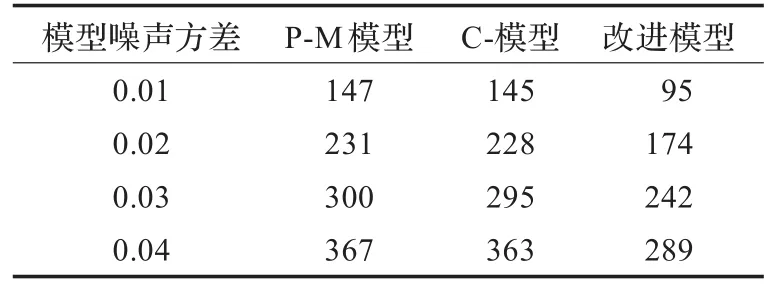
表2 噪声方差不同时各模型的最佳迭代次数

（3）从各模型的相关系数对比图可看出，改进模型的相关系数峰值较其他模型大，而且走势比较平稳。

（4）从表格也可看出，改进模型的峰值最大，而且达到峰值的时间最短，也就是说改进模型去噪时间最短。

（5）随着噪声方差的增加，改进模型在去噪效果方面的优势越来越明显。

7 结束语

在C模型的基础上，改进了各向异性保边缘平滑扩散方程的扩散系数，引入二阶偏导数且自适应的扩散模型。实验结果表明改进模型去噪效果有一定提高。在验证图像效果时，利用相关系数准则来判定改进模型的优越性。

[1]Perona P，Malik J.Scale-space and edge detection using anisotropic diffusion[J].IEEE Transactions on Pattern Recognition and Machine Intelligence，1990，12（7）：629-639.

[2]Witkin A.Scale-space filtering[C]//8th International Joint Conference on Artifical Intelligence，Karlsruhe，West Germany，1983：1019-1022.

[3]冯向初，王卫卫.图像处理的变分和偏微分方程方法[M].北京：科学出版社，2009.

[4]张亶.基于偏微分方程的图像处理[M].北京：高等教育出版社，2004.

[5]Cattle F，Lions P L，More J M.Image selective smoothing and edge detection by nonlinear diffusion[J].SIAM Journal of Numerical Analysis，1992，29（1）：182-193.

[6]王大凯，侯榆青，彭进业.图像处理的偏微分方程方法[M].北京：科学出版社，2008.

[7]Alvarez L，lions P L，Morel J M.Image selective smoothing and edge detection by nonlinear diffusion[J].SIAM Journal of Numerical Analysis，1992，29（3）：845-866.

[8]Chen Yunmei.Image denoising and segmentation via nonlinear diffusion[J].Computers and Mathematics with Applications，2000，39：131-149.

[9]王毅，张良培，李平湘.各向异性扩散平滑滤波的改进算法[J].中国图象图形学报，2006，11（2）：200-216.

[10]朱立新，罗子娟.法曲率驱动曲面演化图像去噪模型研究[J].计算机工程与应用，2011，47（15）：191-193.

[11]冈萨雷斯.数字图像处理[M].2版.北京：电子工业出版社，2007.

[12]Gilboa G，Sochen N，Zeevi Y Y.Forward-and-backward diffusion processes for adaptive image enhancement and denoising[J].IEEE Trans on Image Processing，2002，11（7）：689-703.

[13]Rousseeuw P J，Leroy A M.Robust regression and outlier detection[M].New York：Wiley，1987.

[14]Yu Xiaosheng，Wu Chengdong，Tong Jia，et al.A time-dependent anisotropic diffusion image smoothing method[C]//2nd International Conference on Intelligent Control and Information Processing，2011.

[15]Liu Zhaoxia.New numerical algorithms for the nonlinear diffusion model of image denoising and segmentation[J].IEEE Trans on Applied Mathematics and Computation，2006，178：380-389.

[16]Mrazek P，Navara M.Selection of optimal stopping time for nonlinear diffusion filtering[J].International Journal of Computer Vision，2003，52：189-203.

ZHENG Manman,HU Xiaobing,ZHENG Shenhai

College of Mathematics and Statistics,Chongqing University,Chongqing 401331,China

In the process of image denoising,in order to remove noise effectively and preserve edges and key details,the diffusion coefficient based on the Cattle model is improved and a more effective adaptive denoising model is proposed.The model can not only adopt different diffusion coefficient according to different sizes of the gradient but also lead the edge sharping factor of second order partial deviation into the diffusion coefficient.The best stop time evaluation criteria based on correlation coefficient is proposed in the mean time.The experimental results show that the improved model is superior to C model,and can better coincide with the judge standard.

image denoising;anisotropic diffusion;diffusion coefficient;correlation coefficient

图像去噪过程中，为了在有效平滑噪声的同时较好地保护图像的边缘和细节，在Cattle平滑模型基础上，对扩散系数作出改进，提出了更有效的自适应去噪模型。该模型不仅针对不同的梯度大小采用了不同的扩散系数，而且将边缘锐化因子二阶偏导引入到扩散系数中。而在图像质量评判标准中，提出了基于相关系数函数的最佳停止时间评判准则。实验结果表明，改进的模型优于C模型，且能更好地吻合评判准则。

图像去噪；各向异性扩散；扩散系数；相关系数

A

TP391

10.3778/j.issn.1002-8331.1301-0160

ZHENG Manman,HU Xiaobing,ZHENG Shenhai.Improved model of anisotropic diffusion image denoising.Computer Engineering and Applications,2013,49（18）：130-133.

重庆市自然科学基金资助项目（CSPC，2005BB2197）；重庆大学“211工程”三期创新人才培养计划建设基金资助项目（No.S-09110）。

郑满满（1988—），女，硕士研究生，研究领域为智能计算；胡小兵（1975—），男，博士，副教授，研究领域为现代化技术、机器人控制技术和计算机软件设计；郑申海（1988—），男，硕士研究生，研究领域为智能计算。E-mail：20110602030@cqu.edu.cn

2013-01-15

2013-03-19

1002-8331（2013）18-0130-04

CNKI出版日期：2013-04-10 http://www.cnki.net/kcms/detail/11.2127.TP.20130410.1554.010.html