一类捕食-食饵模型平衡解的整体分歧

权利娜

陕西学前师范学院，西安 710061

一类捕食-食饵模型平衡解的整体分歧

权利娜

陕西学前师范学院，西安 710061

著名的Lotka-Volterra系统在种群动力学理论中具有非常重要的地位，它是1926年由A.J.Lotka和V.Volterra两名数学生态学先驱提出的。在过去的几十年里，经典的Lotka-Volterra模型在生态学理论的研究中占有非常重要的地位，已被广泛关注。以后的许多学者在对其进行不断改进、发展和完善的基础上给出了许多更切合实际的模型，并得到了这些模型的许多重要的相关结论。由于种群间捕食关系的普遍存在，捕食-食饵模型更加受到国内外学者的广泛关注。研究中有的利用极大值原理、上下解方法及全局分歧理论得出了平衡态共存解的存在性、唯一性及其稳定性；有的利用分歧理论、线性特征值扰动理论、稳定性理论得到了带有保护区的捕食食饵模型平衡解的分歧及稳定性等等。在此基础上，一些研究者发现了捕食者具有休眠的这一重要特性并且给出了捕食者具有休眠特性的最低限度模型等，具体内容详见参考文献[1-10]。对于空间分布不均匀的情况有相应的模型：

其中，p，z1表示食饵和捕食者的密度，z2表示能产生休眠卵的捕食者的密度，r，k表示在没有捕食者的情况下的食饵的固有生长率和生存能力，f(p)=cp/(1+chp)为Holling II函数，k1，k2分别表示捕食者处于活动状态的生长率和处于休眠状态的生长率，d1，d2分别表示捕食者处于活动状态的死亡率和处于休眠状态的死亡率，α表示孵化率，捕食者是否进入休眠状态由函数g(p)控制。

本文主要研究休眠卵不孵化（即α=0）的情况。

研究式（1）发自半平凡解的整体分歧。

1 预备知识

记是常用的BanachSpace，={u∈C1u=0，u∈∂Ω}，X=

考虑特征值问题：

其中q(x)∈，则式（2）所有的特征值有下列关系：0＜λ1(q)＜λ2(q)＜L，λ1(q)为主特征值，若p(x)＞q(x)＞0，则λ1(p)＜λ1(q)。

令式（1）中的ν=0，考虑u的边值问题：

记λ0为-Δ在Dirichlet边界下的主特征值，由文献[11]中的定理3.3.28和上下解方法易得：

引理1.2L1的所有特征值均小于零。

证明 因为θ≥0满足(Δ+a-bθ)θ=0，x∈Ω;θ=0，x∈∂θ。记λ(L0)为 Δ+a-bθ的主特征，则λ(L0)=0，又因为L1的主特征λ(L1)＜λ(L0)=0。所以L1的所有特征值均小于零。

引理1.3若(u，ν)为式（1）的非负解u≠0，ν≠0，则

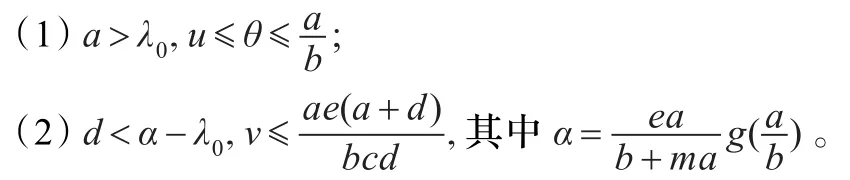
证明（1）在式（1）中的第一个方程的两边同乘以u后积分并运用格林公式得：

（2）同理在式（1）的第二个方程的两边同乘以ν后积分

显然当d≥α-λ0时，式（1）的非负解只能为(0,0)，(θ,0)。

2 非平凡分歧解的结构

记为Δχ+特征值，χ1≥0(x∈Ω)为主特征值对应的特征函数。

下面以d为分歧参数，研究式（1）在半平凡解(d，θ，0)的局部分支。

记w=θ-u，χ=ν，则0≤w≤θ，把w=θ-u，χ=ν代入式（1）得：

易知F=(F1，F2)是连续的，F(0，0)=0，且F的Frechet导数DF|(0，0)=0。

记K=(-Δ)-1，可化为：

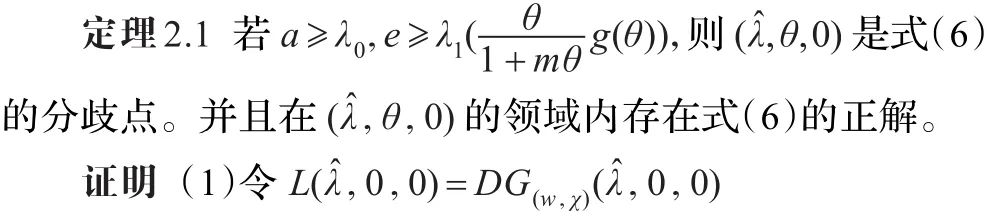
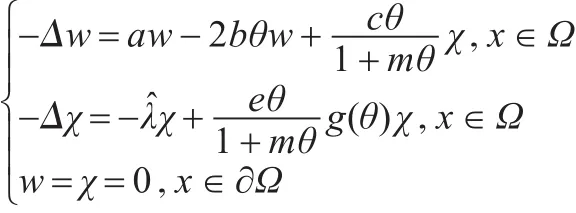
由文献[12]中的定理1.7知：存在δ≥0和C1中的函数(d(s)，ϕ(s)，ψ(s)):(-δ，δ)→R×X使得d(0)=(0)=0，ψ(0)= 0，(ϕ(s)，ψ(s))T∈Z，其中X=(L0，0))，且 (d(s)，w(s)，χ(s))=(d(s),s(w1+ϕ(s)),s(χ1+ψ(s)))满足G(d(s),w(s),χ(s))= 0。因此(d(s)，w(s)，χ(s))(|s|＜δ)是式（2）解的分支。其中u(s)=θ-w(s)=θ-s(w1+ϕ(s))，ν(s)=χ(s)=s(χ1+ψ(s))。

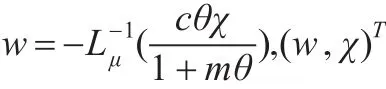
（1）假设d＞，则对于任意的μ≥1，i≥1，d≥di(μ)，所以K(d)没有比1大的特征值，由文献[13]中的定理7.3.9可推出i(T(d，·)，0)=(-1)0=1。

（2）假设d2(1)＜d＜则对于任意的μ≥1，i≥2，d≥di(μ)又因为，所以存在唯一的正数μ1≥1使得d=d1(μ1)，进而可得到：

下面证明R(μ1I-K(d))∩N(μ1I-K(d))={0}。

记K*(d)为K(d)的伴随算子，则K*(d)(w,χ)T=μ1(w,χ)T满足：

由于Lμ1=μ1Δ+(a-2bθ)I可逆，所以w≡0，进而可推出：

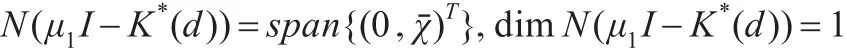
由文献[14]中的定理2.1知：式（1）正解的全局分歧曲线C满足下列两个条件之一：

（1）C在R×X内由点(，0)延伸到∞。

（2）C从点θ，0)延伸到某点(，0)，其中，且I-K不可逆。

下面说明式（1）正解的全局分歧曲线C满足第一个条件。

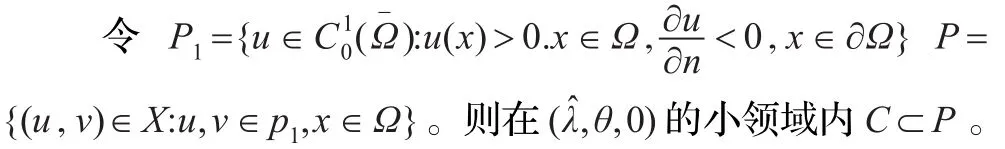
由Lp估计和Sobolev嵌入定理可知：存在{Un}的一个收敛子列Ui使得Ui→u，其中u≥0且≡0。当i→∞时，式（7）变为：-Δu=au，所以a=λ0，矛盾。

（2）假设≡0＞0，有-Δ=-成立。所以=λ0，=χ0，即当m→∞时，dn→-λ0，(un，νn)→(0，χ0)且式（7）可变为：-Δu+cχ0u=au。因为u≥0，由极限原理可得u＞0，x∈Ω，所以a=λ*，矛盾。

（3）假设0，0，由θ的唯一性可知= (θ，0)。所以存在{Vn}的一个收敛子列Vi使得Vi→ν，其中ν≥0且ν≠0。当i→∞时，式（7）变为 -Δν=-，所以有，矛盾。

综合以上可知，C-(，0)⊂P，由引理 2.1知{d:(d，u，ν)∈C}=(-∞，α，-λ0)。从而知C在R×X内由点(，θ，0)延伸到∞。

3 结束语

[1]Ricci C.Dormancy patterns in rotifers[J].Hydrobiologia，2001，446：1-11.

[2]Hairston N G，Hansen A M，Schaffner W R.Τhe effect of diapause emergence on the seasonal dynamics of a zooplankton assemblage[J].Freshw Biol，2000，45：133-145.

[3]Cyllstrom M，Hansson L A.Dormancy in freshwater zooplankton：induction，termination and the importance of benthic-pelagic coupling[J].Aquat Sci，2004，66：274-295.

[4]Carvalho G R.Hughes R N.Effect of food availability，female culture-density and photoperiod on ephippia production in Daphniamagna Strauss（Crustacea；Cladocera）[J].Freshw Biol，1983，13：37-46.

[5]Alekseev V，Lampert W.Maternal control of resting-egg production in Daphnia[J].Nature，2001，414：899-901.

[6]权利娜，李艳玲.一类互惠模型平衡解的分歧与稳定[J].科学技术与工程，2010，10（3）：625-629.

[7]权利娜，李艳玲.一类捕食-食饵模型非常数正解的存在性[J].科学技术与工程，2010，10（28）：6963-6966.

[8]权利娜.一类带有ALLEE影响和病毒传播的捕食食饵模型的正平衡态[J].计算机工程与应用，2011，47（22）：44-47.

[9]谢强军，李艳玲.一类捕食模型正平衡解的分歧和稳定性[J].陕西师范大学学报，2004，32（1）：18-20.

[10]李津，李艳玲.一类反应扩散方程组平衡解的局部分歧及稳定性[J].陕西师范大学学报，2008，36（2）：15-18.

[11]Smoller J.Shock waves and reaction-diffusion equation[M]. 2nd ed.New York：Springer-Verlag，1994.

[12]Baxley J V，Τhompson H B.Nonlinear boundary value problems and competition in the chemostat[J].Nonlinear Anal，1994，22：1329-1344.

[13]叶其孝，李正元.反应扩散方程引论[M].北京：科学出版社，1990.

[14]Wu J H.Global bifurcation of coexistence state for the competition model in the chemostat[J].Nonlinear Anal，2000，39：817-835.

QUAN Lina

Shaanxi Xueqian Normal University,Xi’an 710061,China

Τhe global bifurcation of a positive steady-state solution for a kind of predator-prey model is investigated by the methods of spectral analysis and bifurcation theory.Τhe bifurcation at the positive steady-state solution（θ，0）is acquired by treatingdas a bifurcation parameter.Some sufficient conditions for the existence of positive solution are given.

predator-prey model;global bifurcation;steady-state solution;bifurcation theory;spectral analysis

利用分歧理论和谱分析的方法研究了一类捕食-食饵模型平衡解的整体分歧，得到了在以d为分歧参数的条件下，系统在半平凡解(θ，0)附近出现分歧现象，得到了该模型正解存在的充分条件。

捕食-食饵模型；整体分歧；平衡解；分歧理论；谱分析

A

O175.26

10.3778/j.issn.1002-8331.1111-0487

QUAN Lina.Global bifurcation of positive steady-state solution for a kind of predator-prey model.Computer Engineering and Applications,2013,49（15）：56-59.

陕西学前师范学院科研基金项目（No.2012KJ041）。

权利娜（1978—），女，讲师，研究方向：反应扩散方程及其应用。

2011-11-25

2012-05-28

1002-8331（2013）15-0056-04