三相开关磁阻电机直接转矩控制系统的研究
2013-07-19陈雪波
肖 霄,蔡 森,陈雪波
(辽宁科技大学 电子与信息工程学院,辽宁 鞍山 114051)
0 引言
开关磁阻电机(Switched Reluctance Motor,SRM)是一种结构简单、效率高、成本低廉的新型电机。但开关磁阻电机为双凸极结构,因而电机在运行时易产生噪声和转矩脉动,因此如何减小电机运行时的转矩脉动成为关键问题。
潘再平研究了开关磁阻电机转矩分配函数的控制方法,避免了换相时刻的过流现象,并提高了电机低速运行时的效率,且减小转矩脉动[1]。韩守义采用角度位置控制策略,降低了驱动器件开关损耗,增强了开关磁阻电机在高速运行时的效率,并抑制了转矩脉动[2]。转矩分配函数方法较适合低速控制,角度位置控制更适用于高速控制。
直接转矩控制可以将低速控制和高速控制相结合,使电机在低速和在高速均有良好的运行性能。本文以直接转矩控制理论为基础,结合开关磁阻电机自身特点,采取适合开关磁阻电机的控制方法,该方法是电机产生的磁链控制电机转矩的方向和大小。其方法可以有效地抑制转矩脉动,提高电机性能。
1 SRM直接转矩控制数学模型
1.1 开关磁阻电机的电磁方程
开关磁阻电机的电磁方程为:

其中:U为电机定子端电压,V;R为电机定子电阻,Ω;i为定子电流,A;ψ为定子磁链,Wb;θ为定子与转子相对位置,(°)。
由于电机的定子电阻较小,可忽略。磁链和电压均为矢量,可表示为:

其中:Δt为定子电压施加时间;ψi为当前时刻定子磁链;ψi+1为下一时刻定子磁链;Δψi为定子磁链增量。任何时刻所产生磁链增量Δψ的方向与电源U的方向相同,其幅值大小正比于所加时间Δt的长短。
1.2 转矩与磁链
对SRM的转矩分析可知,电机的电磁转矩等于在任意时间内转子位置变化时对应的电磁能变化率,电机的电磁能可由磁链表达,忽略电机内其他磁能影响,因此电机的转矩T(Nm)可近似表为:

电机的基本电磁方程式中相磁链ψ(θ,i)是电流和转子位置的非线性表达式,其非线性磁链的偏微分形式为:

由于电机定子电阻较小可忽略,将式(5)表达为:

其中:转子转速ω=,rad/s,电感
由式(7)可知,电流与磁链有一个一阶延迟环节,可认为当磁链变化时,电流为常量,因此可由定子磁链控制电机转矩;再由磁链和电压的关系可知,磁链方向和大小可由电压矢量控制[3],因此由外加电压矢量的方法可求得期望转矩。
2 功率变换器结构与空间电压矢量
2.1 功率变换器结构
本文采用不对称半桥式电路作为控制系统的功率变换器主回路[4],以三相6/4极电机为研究对象,其三相绕组之间相互独立,每个桥臂由2个主开关器件和2个续流二极管以及电机的一相绕组组成,如图1所示。
以A相绕组为例:当T1与T2同时触发时,A相绕组承受正向电压,此时电压矢量状态定义为“1”;当T1阻断、T2触发时,假定A相绕组上有电流,电流将缓慢下降,此时电压矢量状态定义为“0”;当T1与T2同时阻断,绕组电压反向时,绕组上电流会迅速降低为零,此时电压矢量状态定义为“-1”。对于三相开关磁阻电机,共有27种开关状态,考虑到电机运行时不能有两相同时触发,因此一些矢量组合是不合适的,如(1,1,1)等。因而选定了符合条件的6个幅值相同且相位相差60°的电压矢量,分别为U0(1,0,-1)、U1(0,1,-1)、U2(-1,1,0)、U3(-1,0,1)、U4(0,-1,1)、U5(1,-1,0),这6组矢量将整个区域划分成N0~N5区域,每一个区域占60°,保证磁链和转矩处于每个控制区域中,如图2所示。

图1 开关磁阻电机功率变换器结构
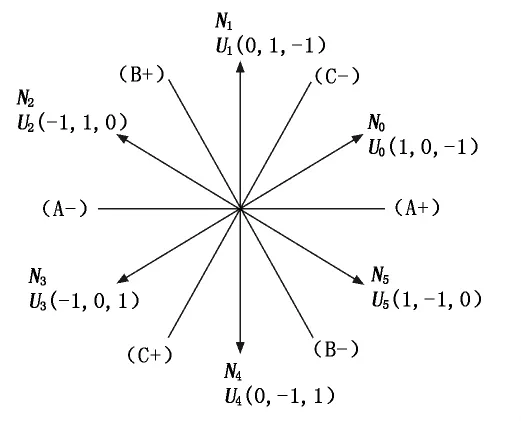
图2 电压空间矢量分布图
2.2 磁链矢量坐标变换
开关磁阻电机直接转矩控制理论中,需确定磁链的空间位置,以判定所用电压矢量。为得到SRM三相合成的定子磁链,将三相定子磁链经矢量变换得到静止α-β坐标系,公式如下:

其中:ψα、ψβ、ψA、ψB、ψC为磁链矢量,Wb。磁链幅值和磁链矢量角定义为:

由式(10)、式(11)可计算出实际磁链在空间6个扇区的位置。转矩符号完全由磁链偏微分决定,与相绕组电流方向没有关系。若定子磁链对转子角度的变化率为正,则转矩符号为正,转矩增大;反之亦然。
由磁链和电压的关系可知,定子磁链的大小与方向要与所加电压空间矢量的组合相一致。例如:定子磁链位于N0的扇区内,选择U1、U2转矩增加,U4、U5转矩减小。以此类推,在扇区Nk内(k=0,1,2,…,5),选择Uk-1、Uk-2转矩减小,Uk+1、Uk+2转矩增大。因此,得SRM磁链与转矩调节表,见表1。

表1 磁链与转矩调节表
3 仿真
3.1 MATLAB仿真模型
在MATLAB/Simulink仿真环境下,建立SRM直接转矩控制模型,如图3所示。
模型中采用60kW三相开关磁阻电机,给定转矩和给定磁链分别为10Nm和0.3Wb,转矩和磁链的滞环带宽分别设为±0.1Nm和±0.1Wb。模型中将电机转矩、磁链估算值与给定转矩、磁链分别进行比较,其差值输入滞环比较器,根据磁链和转矩的变化趋势,由相应的开关表选择触发信号,驱动功率变换器。
3.2 结果分析
转矩和磁链给定值为常数时,MATLAB仿真结果如图4、图5所示,可见直接转矩控制可保持磁链的幅值基本恒定,且磁链运行轨迹呈圆形。
转矩给定为阶跃信号时,仿真结果如图6所示。图6中,在0.05s时负载由0Nm突然增加到10Nm时,采用直接转矩控制对电机输出转矩曲线进行调节,使其在极短的时间内达到实际要求的转矩,且输出转矩平稳、脉动较小。
4 结论
传统电流斩波控制中,未把转矩作为直接控制量,转矩脉动较大。根据开关磁阻电机的特点,可把直接转矩控制理论与开关磁阻电机相结合,通过电机磁链控制电机转矩,使转矩控制在期望范围之内。控制过程中,应根据构建的磁链与转矩调节表,选择相应的电压矢量以确定磁链矢量,从而控制磁链方向和幅值。仿真结果表明,该方法可有效改善开关磁阻电机的动 态与稳态性能。

图3 MATLAB仿真模型结构图
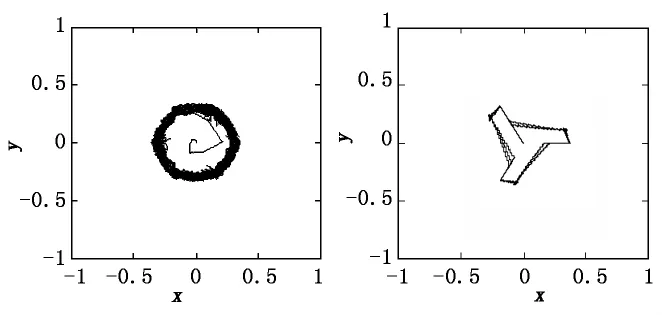
图4 直接转矩控制的磁链轨迹 图5 电流斩波控制的磁链轨迹

图6 直接转矩控制仿真图
[1]潘再平,罗星宝.基于迭代学习控制的开关磁阻电机转矩脉动抑制[J].电工技术学报,2010,25(7):51-55.
[2]韩守义,赵德安.开关磁阻电机角度位置的纯硬件控制[J].微计算机信息,2008,24(5):51-52.
[3]杨玉岗,姚若萍.开关磁阻电机动态性能的研究[J].清华大学学报,1997,37(9):82-85.
[4]王宏华.开关型磁阻电动机调速控制技术[M].北京:机械工业出版社,1999.
