基于Multisim 的混沌电路仿真实验

2013-07-19杜宇上

实验室研究与探索 2013年1期

杜宇上，肖化

(1.华南师范大学物理与电信工程学院，广东广州510006;2.广东工业大学实验教学部，广东广州510006)

0 引言

混沌是非线性系统的典型行为，越来越多的院校已将混沌理论与实验引入到大学物理实验中［1］，电子线路系统可以模拟出混沌效应［2-3］。在目前物理实验中，常利用混沌电路作为非线性系统实验的教学内容。

在实验教学的过程中，往往采用已经设计制作完成的电路实验板或者计算机数值模拟得以实现［10-11］。然而，由于电路实验板上的电路元件数量和型号的限制，参数可调节范围有限，采用电路实验板完成混沌电路实验教学会出现教学内容呆板，不利于促进学生在自主学习中探索;而计算机数值模拟手段经常采用Matlab、C 等编程语言，通过建立数学模型、方程离散化和编写程序来完成实验［12］，学生需要先掌握对应的编程语法和数学模型构建，这将增加学生学习的难度，未必能保证学生得到正确的实验仿真结果。

相比传统的混沌电路实验板，采用Multisim 学生可以自由地修改电路参数并实时观测实验现象;相比Matlab、C 等编程语言，采用Multisim 完成混沌电路实验教学，学生不需要建立数学模型和编写程序，只需要在界面中利用软件图形化的功能搭接电路。这将方便学生操作，使学生更易于自主修改实验模型，有助于学生开展探究性学习，发挥学生学习的自主作用。

本文提出了在实验教学中采用Multisim［4-9］进行混沌电路实验的方法，为提高学生的学习效率，开展探究性学习提供可行的实验工具。

1 混沌电路的原理及设计

蔡氏电路为混沌电路的典型例子，其结构简单、现象明晰，被广泛用于高校的实验教学中。蔡氏电路原理图如图1 所示［3］。电路由1 个线性电感L、2 个线性电容C1、C2，1 个线性电阻R0，1 个非线性电阻R 构成，为三阶自治动态电路，即分为LC 振荡电路、RC 分相电路和非线性元件三部分。电阻R0起调节C1、C2的相位差。非线性电阻R 为分段线性电阻，伏安特性iR=g(uR)，如图2 所示。

图1 蔡氏电路基本原理图

图2 非线性电阻的伏安特性

根据基尔霍夫定律，由图1 可得出电路状态方程:

由于R 为非线性电阻，上述方程组没有解析解。该电路在特定的参数条件下出现自激振荡动态过程，出现混沌现象。

集成运算放大器可构成如图3 所示的负电阻电路［13］，实现了分段线性电阻的功能，其伏安特性如图4 所示。因此根据文献［14］，图1 中非线性电阻R 的等效电路可由图3 所示的电路并联得到，等效电路如图5 所示，为有源负阻非线性电阻，其作用是使振动周期生分岔和混沌等一系列非线性现象。

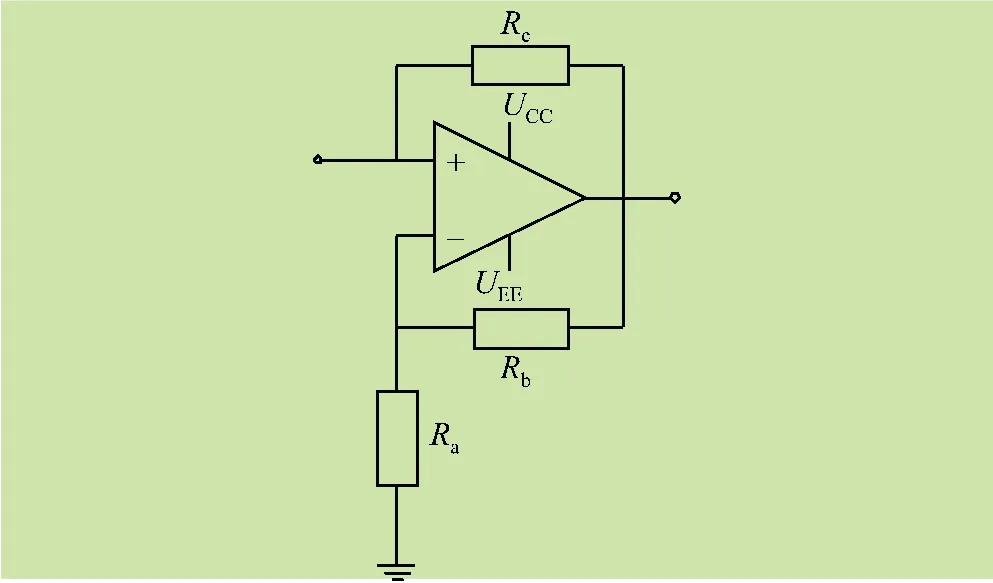
图3 负电阻电路

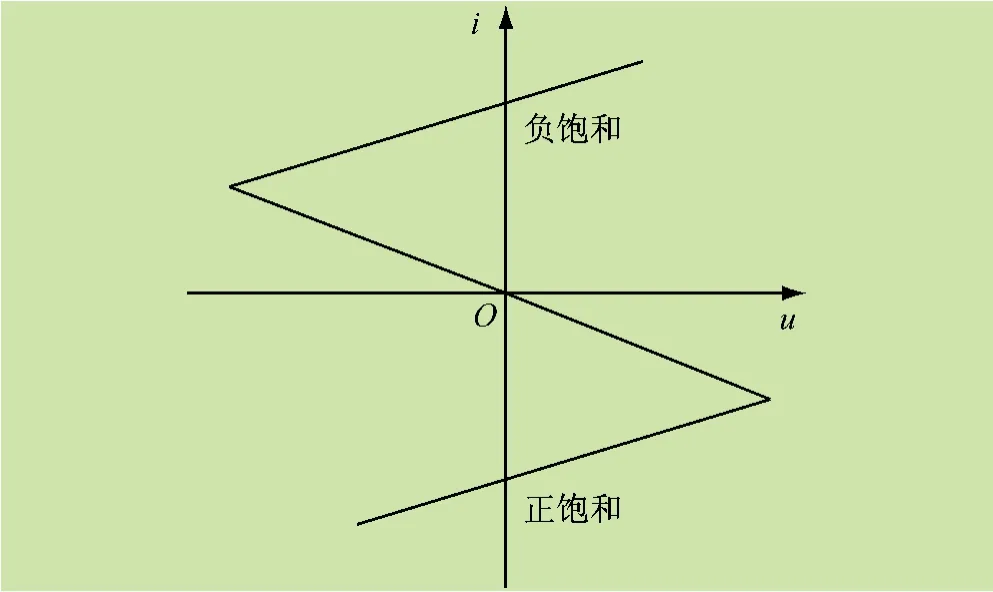
图4 负电阻电路的伏安特性

图5 非线性元件的等效电路

2 混沌电路的构建与仿真

2.1 实验电路的构建

综合图1 和图5，在Multisim 平台上构建如图6 所示的实验电路。电路中元件参数为:L1=18 mH，C1=10 nF，C2=100 nF，R1=3.3 kΩ，R2=R3=22 kΩ，R4=2.2 kΩ，R5= R6=220 Ω［15］。其步骤如下:运行Multisim，新建一个空白的仿真文件;在“基本元器件库”中选择对应参数的电阻、电容、电感、电位器，在“模拟电路器件库”中选择运算放大器，在“电源库”中选择直流电压源和接地端;分别将这些元器件放置在工作区，并设置元器件参数;用鼠标完成元器件间线路的连接;为了观察混沌电路的波形，在仿真平台上添加一台虚拟示波器，将示波器A、B 两个输入通道与需要观测的电路节点相连，通道A观测电容C2两端的电压信号;通道B 观测电容C1两端的电压信号。

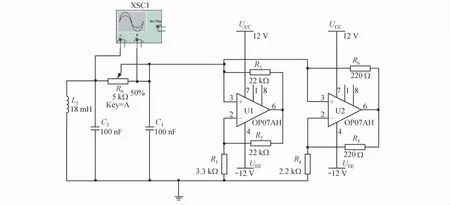
图6 在Multism 平台上构建的混沌电路

2.2 实验电路的仿真

运行软件，用鼠标双击双踪示波器的图形，在弹出示波器波形显示窗口上选择“Y/T”模式，进行波形的时域分析;选择“A/B”模式，则显示李萨如图形，进行波形的相位测试。

R0的作用是移相，使电容C1和C2两端的电压信号产生相位差;运放的前级和后级的正、负反馈同时存在，正反馈的大小程度与R0、R3、R6有关，负反馈的大小程度与R1、R2，R5，R4有关，若调节R0的阻值大小，正反馈的大小程度就会发生变化，当正反馈程度大于负反馈程度时，电路才能处于振荡状态［15］。

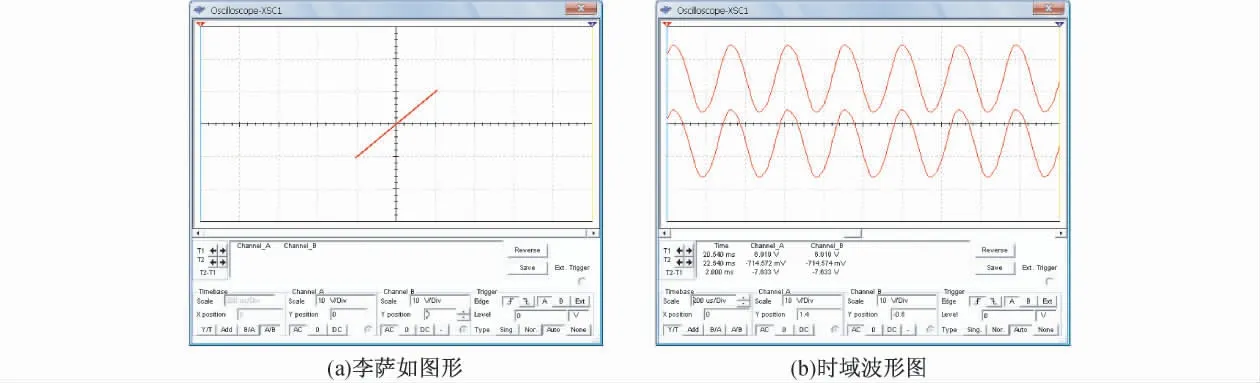
图7 R0 =0 时的仿真结果

图8 R0 =1 kΩ 时的仿真结果

图7 ～9 分别为R0阻值为0、1、1.5 kΩ 时，示波器观测得到的李萨如图形和时域波形。当R0阻值最小时，如图7 所示R0=0 时，观察到的李萨如图形为一条直线;再调节R0阻值，当R0=1 kΩ 时，如图8 所示观察到单涡旋吸引子集的图像;继续调节R0阻值，当R0=1.5 kΩ 时，如图9所示观察到双吸引子集的图像，也就是“蝴蝶”图像，由时域波形可看出了混沌振荡的非周期性。由图7 ～9 可以知道，在实验教学中应用Multisim 对混沌电路进行仿真是可行的。

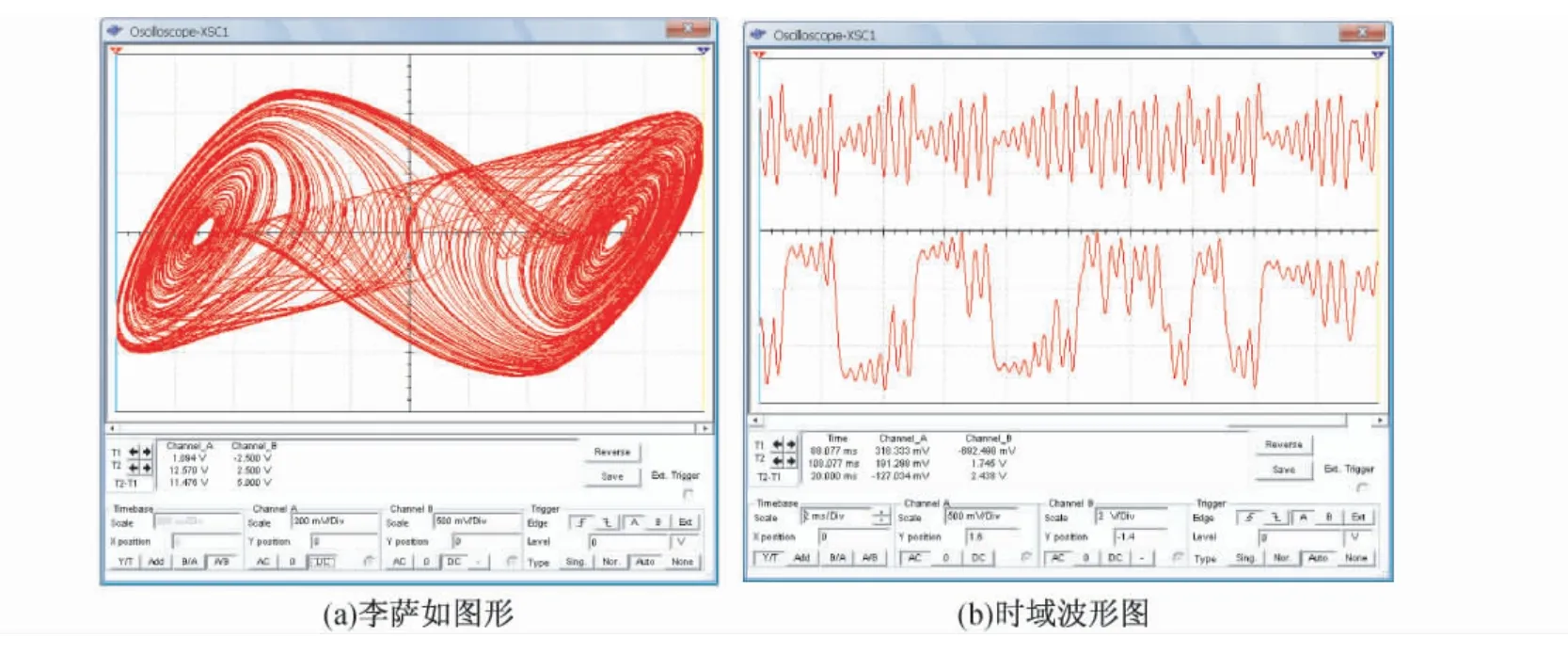
图9 R0 =1.5 kΩ 时的仿真结果

3 结语

计算机仿真软件在实验教学中毕竟是一种辅助工具［16］，不能夸大它的作用。培养学生的动手能力、实验仪器操作能力、排除故障能力，也是实验教学的重要目的，这是计算机仿真软件很难实现的效果。我们可以采用“理论分析—仿真—实验验证”的方法［17］，在实验教学中将计算机仿真实验与实物实验相结合，使用仿真软件引导学生学习，提高学生的实践能力。

实践表明，在高校的实验教学中引入诸如Multisim 软件的EDA 仿真软件，对于提高学生的学习效率和效果、降低教学成本、启发学生思考及培养学生的分析问题能力、促进学生的自主学习等方面起到积极作用。

［1］安迪，高媛媛，姜凤怡. 滤波法控制混沌的电路实验［J］. 物理实验，2011，31(9):34-36，40.

［2］危雨轩，段书凯，熊灵，等. 基于混沌电路的同步控制实验箱的设计［J］. 西南师范大学学报(自然科学版)，2010，35(4):169-174.

［3］包伯成，王其红，许建平. 基于忆阻元件的五价混沌电路研究［J］. 电路与系统学报，2011，16(2):66-70.

［4］彭端. 电路与电子技术仿真实验教程［M］. 广州:世界图书出版公司，2010:3-7.

［5］郭丽颖. 基于Multisim 的彩灯循环闪烁电路设计与仿真［J］. 实验室研究与探索，2010，29(7):187-189.

［6］吴贞焕，钟庆宾，张新莲. 负反馈放大电路稳定性动态仿真研究［J］. 实验室研究与探索，2011，30(7):34-36，53.

［7］余群，舒华，陈新兵. Multisim 进行电子电路设计的教学研究［J］. 实验科学与技术，2007，5(5):118-120.

［8］江有永. Multisim 和Excel 在二极管特性实验教学改革中的应用［J］. 实验技术与管理，2011，28(2):106-109.

［9］罗倩. Multisim 仿真软件测量电流的新方法［J］. 实验技术与管理，2008，25(12):99-101.

［10］吴先球，熊予莹. 近代物理实验教程［M］. 北京:科学出版社，

2009:311-318.