通过游标卡尺培养学生的思维迁移能力

欧阳映

（华东师范大学物理系，上海 200241）

在传统的教学中，学生学习的知识是支离破碎的，学生具有了很多的“死知识”，却不能在社会实践中很好的应用，而所谓知识的应用，实质就是知识和方法的迁移.迁移是一种学习（包括知识、动作技能、思维方法、学习态度和情感）对另一种学习的影响；两种学习相互干扰是负迁移，两种学习相互促进是正迁移.［1］教师应遵循学习迁移规律，尽量促进正迁移，抑制或避免负迁移.在物理教学活动中，教师不仅要传授专业必备的理论知识与技能，更应该培养学生物理思维及迁移能力.本文以游标卡尺为例，循序渐进地探讨如何在物理教学中创设情境，帮助学生迁移运用所学知识来解决不同情境、不同领域当中的问题.

1 游标卡尺中蕴含的测量思想和方法

游标卡尺为长度测量的精密工具，它蕴含的物理思维和方法能够启发学生的思维意识.游标卡尺成功地解决了长度测量上的一个难题，需精确测量的微小长度量和人眼有限分辨能力之间的矛盾，如图1所示（精度0.1mm的游标卡尺原理示意图），它利用主尺与游标尺上的每一最小分格之差，把不易直接测量的微小量，通过“放大”显示成容易测量的较大量，从而提高测量精度.游标卡尺放大测量思想的关键是对比、作差、转移放大，若学生习得此思想方法，并将它迁移运用到其他类似的问题情境中，将会提高学生成功解决问题的概率.

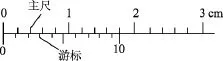
图1

2 “为迁移而教”——游标卡尺的简要教学策略

“为迁移而教”的理念要求我们，在教学实践中重视培养学生的概括能力，让学生学会从内容中抽象概括，找出事物的本质.［2］为避免学生“一叶障目不见泰山”，只会机械模仿而不知其缘由，教师必须充分调动学生学习兴致.教学过程中，教师首先让学生感知物理问题，对问题形成表征后，再引导学生讨论问题解决方略——游标卡尺测量思想的教学.此时，教师或“让学生动手——经历简易游标卡尺的制作过程”，［3］体验和感悟游标卡尺测量的细微程度，或借助课件演示，图文并茂又对照实物去研究等不同教学策略，最终让学生领悟并概括游标卡尺的放大测量方法.教师通过适当的教学策略，让学生探讨游标卡尺的内在测量机制，最后对所习得的知识方法概括化、系统化，便于学生形成知识的横向和纵向迁移.

3 游标卡尺测量方法在各个阶段的迁移运用

根据学生思维发展的特点，学生对游标卡尺测量方法的思维迁移模式，可按阶段分为建模阶段、确立阶段和深化阶段.［4］初中阶段，学生正由形象思维开始向抽象思维转变，此阶段可谓是建模阶段；高中阶段，学生的逻辑推理、归纳和演绎等思维能力不断提高，此阶段可谓确立阶段；大学阶段，学生已具备较强的抽象思维能力，此阶段可谓深化阶段.

3.1 初中阶段的迁移——建模阶段

在建模阶段，主要使学生对游标卡尺测量方法形成感性认识，培养其物理形象思维迁移能力.教师在学生已对游标卡尺测量方法有了概括性认识的基础上，创造形象化的物理情境，让学生初步建立迁移模型.

情境1.介绍了精度为0.1mm、0.05mm和0.02mm的游标卡尺之后，即可引发学生思考：如何进一步提高游标卡尺的精度到0.01mm.学生在类比迁移的基础上可快速作答：把游标尺标准的99mm分成100等份，则游标尺和主尺每一最小分格差为0.01mm，即游标卡尺的精度为0.01mm.［3］该情境知识和已学知识为同一层次，它们之间的迁移称为知识学习之间的横向迁移，而且该情境知识和已学的知识也较为相似，故也称为知识学习之间的近迁移，该种迁移现象较容易出现.

情境2.学完了“长度的测量”一章的内容后，教师可让学生思考以下问题：现有一把标准米尺和一把刻度均匀但不准确的米尺（该尺标准长度为0.98m），如何只用刻度不准确的尺子测量出桌子的高度.学生在脑海中搜索已学相关知识，经类比，找到应对策略：先比较两把尺子，确定不准确尺子的实际长度，再换算到每一最小刻度代表的实际长度（0.98cm），再用该尺子去测量桌子的高度，最后运用数学公式计算测量结果.该情境知识和已学知识有在形式上具有一定的相似性，但需要学生抽象物理模型，并在类比中移植.

情境3.初中生学习了摄氏温标后，知道1atm下，冰水混合物的温度为0℃，沸水的温度为100℃.教师可让学生思考：如何用一支未定标的温度计来测量某种液体的温度.学生同样可迁移运用游标卡尺的测量方法来解决该问题.该情境知识较情境2中的知识又深一层次，和已学的知识情境较不相似，称为知识学习之间的远迁移.

此阶段，教师需遵从学习迁移的循序渐进性，可引导学生直接追溯游标卡尺测量方法的形成过程，通过板书画图等形象化手段，帮助学生对新的问题进行分析整合，抓住主要因素而忽略次要因素，就可以使学生经过物理形象思维的过程，逐渐形成思维迁移轮廓.

3.2 高中阶段的迁移——确立阶段

在确立阶段，主要培养学生的物理抽象思维迁移能力.要求学生借助观察到的物理现象和记录的物理数据，利用物理抽象思维，在比较中变通，在分析中转化，找出物理现象和物理数据之间的对应关系.此阶段，教师需创造抽象化的物理情境，让学生关注事物本质，使学生从形象化思维迁移转变为抽象化思维迁移.

情境4.在“用打点计时器测定匀变速直线运动加速度”的实验中，得到一段记录纸带如图2所示，求物体运动的加速度.

图2

教师逐步引导，向学生展示物理抽象思维的全过程，学生逐层分析、推理并作出判断.在对比迁移的基础上，学生经历以下思维过程.

（1）逻辑分析.打点计时器每0.02s在纸带上打一点，纸带上每相邻两点的距离表示匀变速直线运动物体在相等时间间隔内走过的距离.由于打点计时器在纸带上打点的瞬间，纸带运动的瞬时速度未知，则需要推导只含位移s、时间t、加速度a而不含速度v的公式.

（2）运用基本公式.打点计时器的打点周期为t＝0.02s，由匀变速直线运动规律，则纸带上每一点到起点的位移s为

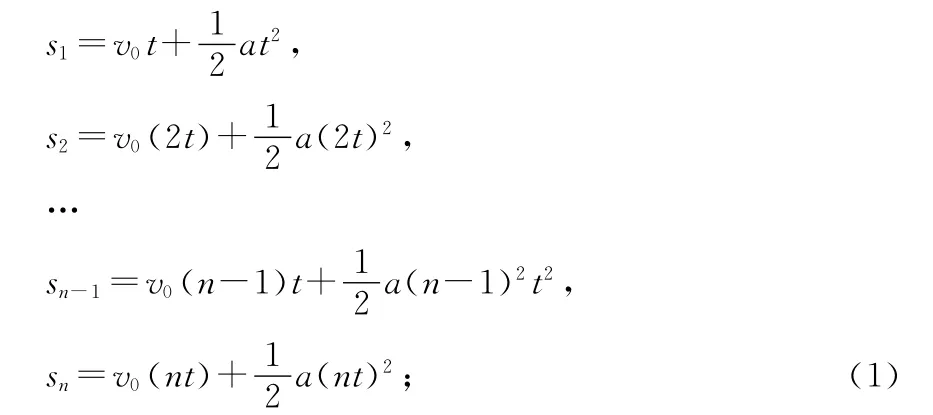
则纸带上每相邻两点之间的距离s为

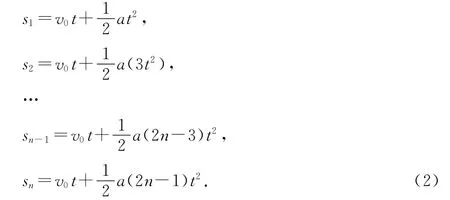
（3）比较作差，消去v0，则有纸带上相邻两点之间的间隔差为

（4）放大时间间隔.由于t＝0.02s，增加了计算的复杂度，则取T＝5t＝0.1s，对时间放大，减小计算量.此时取每连续5小段作为一大段，则可得每相邻两段之间的间隔差为

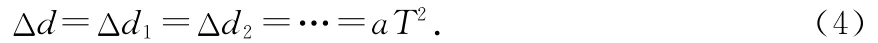
现只要用刻度尺测量出每一大段的长度，代入推导公式（4）即可求解.

以上解决问题方法称为逐差法.逐差法和游标卡尺测量的思想方法具有高度相似性：对比——作差——转移放大.思想方法能够形成迁移的标志在于它的高度概括性，而且思想方法的高度抽象性有助于形成远迁移，因为相同的抽象元素可以在很不相似的情况下出现.［1］此种迁移现象与反复练习而获得的技能自动化迁移不同，它具有高度抽象性，我们也把该迁移现象称为高通路迁移.此阶段，教师应鼓励学生进行逻辑抽象分析，关注事物的内在联系，让学生成为知识的“探索者”.

3.3 大学阶段的迁移——深化阶段

深化阶段为高通路迁移的多发阶段，学生通过综合训练物理思维并充实知识结构，使方法策略性知识顺应到认知结构中，形成有效思维迁移，并实现知识创新.此阶段，教师应创造开放性的学习环境，鼓励学生联想思维和发散思维，对已建立的思维迁移模式进一步思维加工和梳理，以便深化运用和推广.

情境5.将游标卡尺的测量方法迁移到用拍频法测量超声波频率的研究和学习中.

拍频法的测量原理，如图3所示.频差较小、速度相同的两列同向共线传播的简谐波相叠加即形成拍，拍频波的频率（即拍频）是相叠加的两列简谐波的频差.目前已有用拍频法制作的超声波频率测量仪，通过步进键盘调节频率的大小，近似测量超声波的频率.［5］测量时，由信号发生器产生一列可调的参照超声波和一列未知频率的超声波，经过加法器叠加；逐渐调节参照波的频率，使两列超声波的频率接近，便获得到稳定的拍频波；只要测量拍频波的频率，对照参照波就可知道待测波的频率.拍频现象实际上也体现了对比—转移—放大的思想，它把高频信号中的频率信息转移到差频信号之中，使得难以测量的高频信号转变为容易测量的低频信号.拍频法还可以应用于光速的测量，因为差频波不仅记录了频率信息还记录了相位信息，通过比较相位的方法可以间接地测定光速.

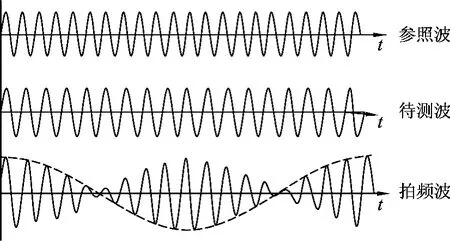
图3

长度的测量、频率的测量与光速的测量，看似不相关，但都可以采用类似的方法进行测量.因此，有意识地培养学生思维意识，让学生发现问题，面对新的问题情境，让学生进行联想思维，突破问题束缚，促进学生思维迁移，从而更有效地解决问题.［4］

4 结语

要使以上游标卡尺测量方法在各阶段的迁移运用策略能够实行，需学生在初中阶段就习得游标卡尺的测量方法，并加以内化.由于学生思维发展的速度各异，教师应针对学生具体情况采用不同的迁移教学策略.迁移的产生要经过复杂的认知活动，审题与联想、分析与类化、抽象与综合、概括与归纳等，是学习迁移过程中不可缺少的基本认知活动.［6］方法策略的迁移并非一蹴而就，它是一个循序渐进的内化过程.为促进学习迁移，教学中应要求学生准确理解已学知识，鼓励学生自己总结和归纳学习经验，在此基础上运用已学知识去解决问题.此外，教师要不断创设与应用情境相似的学习情境，实现学习的近、远迁移，横、纵向迁移，以便更好地促进学生发展.

1 D.N.Perkins，G.Salomon.Transfer of Learning.Oxford，England：Pergamon Press，1992.http：／／learnweb.harvard.edu／alps／thinking／docs／traencyn.htm.

2 叶宁.迁移理论在线性代数教学中的应用策略.新课程研究，2011，11（240）：81－83

3 项其杰.游标卡尺教学中不应该被忽视的几个环节.中学物理，2011，29（7）：17

4 胡景勤.高中物理思维迁移教学的研究.学位论文：陕西师范大学，2007.

5 姚计军，欧夕晨，邱选兵，王青狮.基于超声波可调谐拍频的产生及应用研究.山西电子技术，2011（1）：7－8

6 王华丽，卢梦克.论迁移理论在物理教学中的应用.教学管理，2010（9）：138－139