M/M/1/∞/∞/PS强拆继续型系统的优先权决策优化

李华嵩，罗兵，余健松



M/M/1/∞/∞/PS强拆继续型系统的优先权决策优化

李华嵩，罗兵，余健松

（五邑大学 信息工程学院，广东 江门 529020）

将风险函数统计引入处理M/M/1/∞/∞/PS信息系统规划的优先级决策问题，利用一致最小风险函数评估行动空间中系统决策的损失期望，从而在设计大规模通信系统时降低损失风险，以确保系统长期运转的安全合理性.

系统优先权；信息队列处理；信息优先策略

现代智能电网与物联网对系统的控制本质上可以理解为一个个信息服务平台对各自要求服务的信息队列的处理控制问题.

目前对于信息系统队列的论述文献很多都集中在特定服务条件下的队长及排队结构分布方面[1-2]，近些年来也逐渐出现了利用排队理论解决信息系统的优化问题，如文献[3]利用数字排队调度系统模型对失效率进行分析，从而对系统可靠性进行预测. 文献[4]采用基于P-Aloha多址通信技术进行RFID系统的反碰撞处理，用排队论中的M/D/1队列模型对通信处理过程进行建模分析，对RFID的重发、应答器数量的优化设计进行了仿真. 文献[5]利用排队论对数据帧排队延时及丢包建立基于以太网通信损失代价的数学模型，并利用边际法计算出目标函数取极值时的最佳队列长度实现系统队列优化.

由于通常情况下服务台难以控制通信队列的通信质量、信源和队列长度，因此上述文献算法在工程中的应用受到限制. 而利用排队论优化服务台信息优先级策略方面的论述较少，因此本文在上述文献的基础上，利用风险函数解决M/M/1/∞/∞/PS的服务台优化安全问题，研究如何引入统计决策的一致最小风险函数用以制定系统的服务台的优先级最优决策方案，并应用于实际工程的通信系统设计中.

1 系统信息的排队特征分析

在设计服务台机制的信息服务系统的优先级服务策略时，总是假定请求信息的到来服从一定的先验概率分布. 且通常采用肯德尔方法用下述符号来定义排队系统的性质：

其中①为信息到达时刻的概率分布；②为服务时间概率分布；③为服务台的个数；④为请求信息源的总数；⑤为系统内信息队列的容量；⑥为队列服务处理的原则，若⑥缺省则认为队列处理的原则为FIFO原则（先进先出原则first-in-first-out），若⑥为PS则为优先级服务原则.

由于具有优先权信息队列的处理顺序仅与当前状况有关，而与历史无关，因此整个系统可以看成是一个马尔可夫链下的生灭过程. 信息系统的服务台优化策略是指定分类信息的优先级来实现的，假定一个最简信息服务系统：信息到达时刻与服务时间均服从马尔科夫概率分布，信息源的总数与信息队列的容量均为无限多，仅有一个服务台，其信息服务机制为优先级服务，则队列系统表述为M/M/1/∞/∞/PS.

通常赋予某类信息优先级的策略有两种[6]，一种是强拆型优先权，一种是非强拆型优先权.

定义1 假定队列系统中A类信息具有高于B类信息的优先权，若A类信息到达时，无论当前信息处理是否完成，系统服务台都中断当前对B类信息的服务处理，转而对A类信息进行处理，该优先权称为强拆型优先权 (PPDQ，Preemptive Priority Discipline Queue) .

非强拆型优先权是当A类信息到达时，等待服务台执行完当前B类信息的处理，再对A类信息进行处理.

为论述方便，本文将PPDQ强拆型优先权系统也简称为两类：一类为强拆继续型优先权系统（PPSCDQ，Preemptive Priority and Service Continuous Discipline Queue），该类系统服务台在中断低优先权信息服务转而对高优先权信息进行服务完成后，恢复到对低优先权的信息服务时，服务从前次服务的中断点开始执行，即强拆继续型优先权系统. 另一类为强拆重复型优先权系统（PPSRDQ，Preemptive Priority and Service Repeat Discipline Queue），该类系统服务台在恢复到对低优先权的信息服务时，服务从被中断服务的信息服务过程的初始阶段开始执行.

2 统计决策的风险函数分析

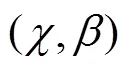
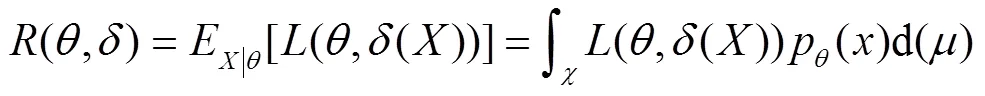
3 通信信息队列的优先权决策优化处理

3.1 优先权处理优化的流程

将统计决策的风险函数概念引入M/M/1/∞/∞/PS信息队列系统，可实现优先权策略的优化. 在对优先权策略进行风险函数评估之前，需要做一些准备工作，包括对信息的初步简化分类，信息先验概率的估算等等. 本文提出的优化处理流程如图1所示.

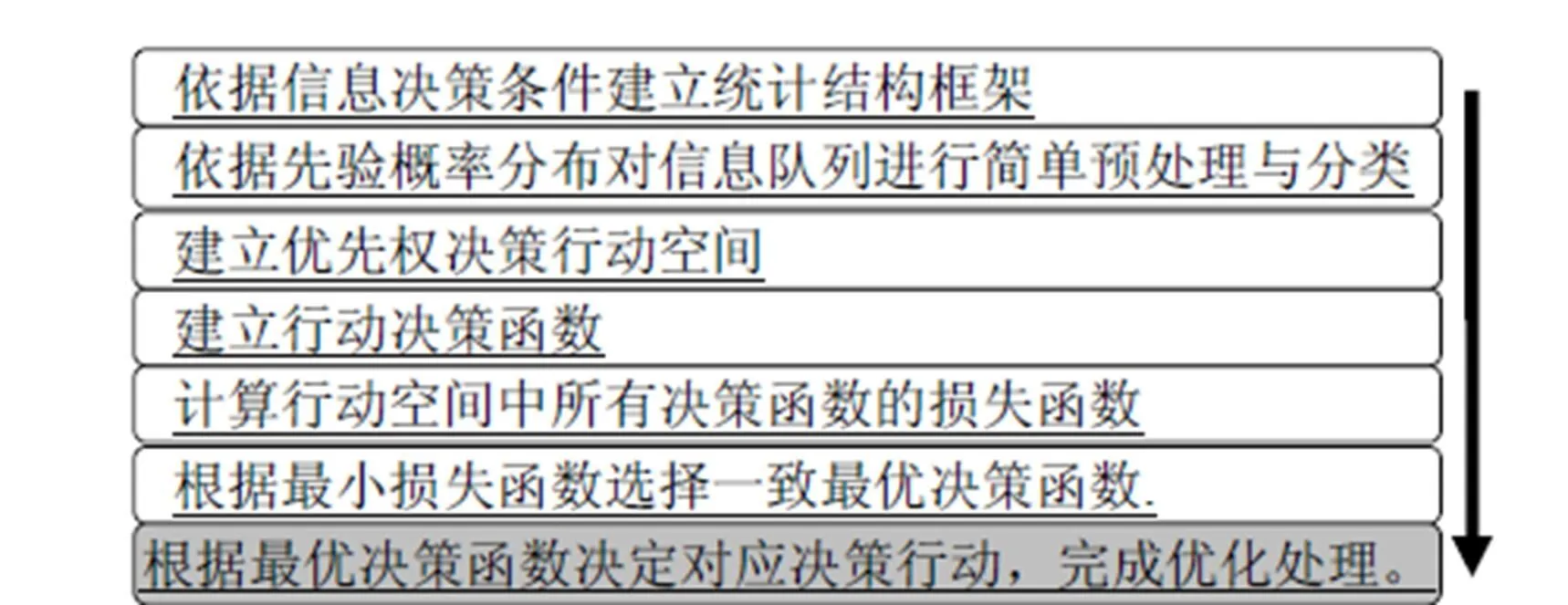
图1 信息队列优先权决策优化过程

实际上整个优化过程中，处理工作量最大的一步是在依据先验概率分布对信息队列进行简单分类预处理. 根据风险函数定义，本文可以给出以下推论：

以上两个条件在现实中很难完全相同，主要原因是实际控制现场不确定因素较多，很多情况下无有效的先验样本且无先验概率分布可追寻. 因此优化过程中需要对频率与损失影响相近的几类信息做近似处理.

3.2 优先权信息队列分布分析

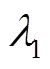
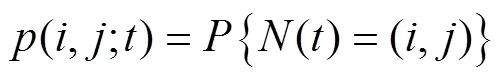
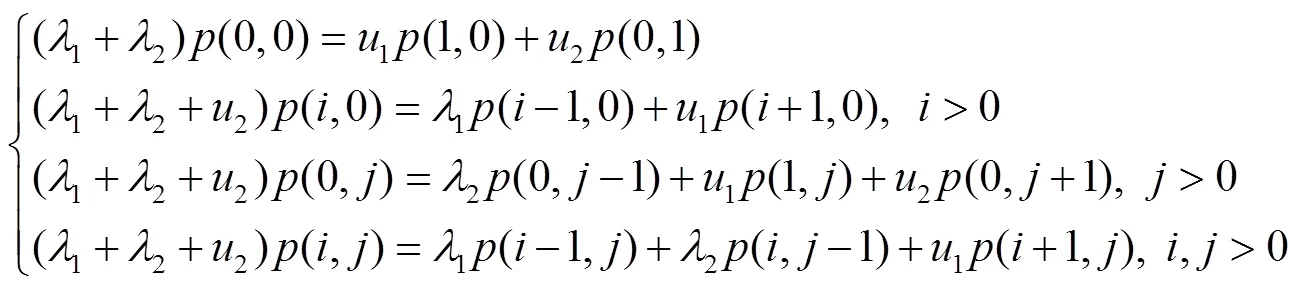
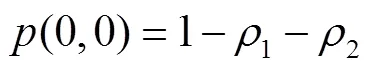
等待信息队列中A类信息数量的分布概率为：

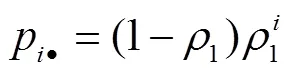
同时B类信息在等待信息队列中的平均值为：

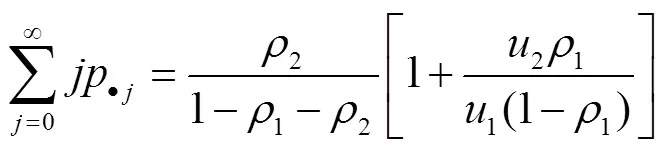
该结果与M/M/1/∞/∞/PS信息系统常识一致：低优先权信息的存在对高优先权信息的队列长度无影响，而高优先权信息的分布对低优先权信息的队列长度产生了影响.

3.3 一致最小风险函数与决策优化的应用

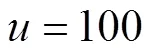
表1 示例3类信息的分布情况

决策目标描述为：若优先权A具有高于优先权B的强拆继续型优先权，为1、2、3类信息赋予A或B优先权使得系统的损失数学期望值最小.

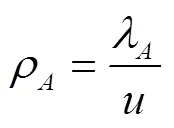
由于B类信息在队列中的存在不影响A类信息的处理等待，因此由式（5）得具有A类优先权的信息在系统队列中等待时长的数学期望为：

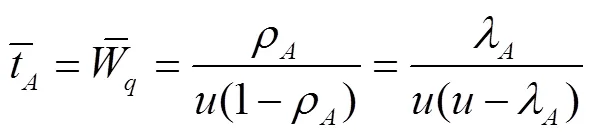
由式（6）得具有B类优先权的信息在系统队列中等待时长的数学期望为：

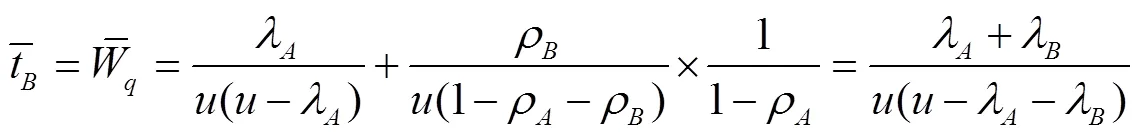
根据定义3的损失函数定义有:

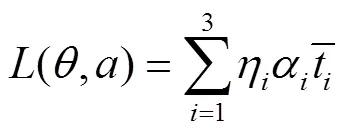
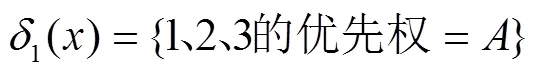
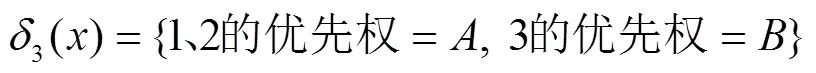
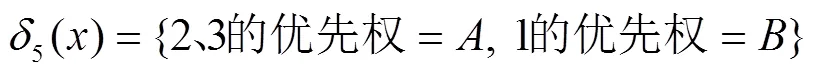
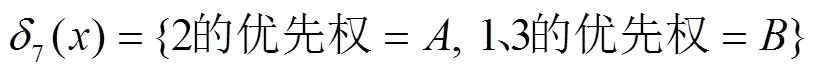
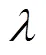
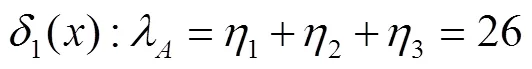
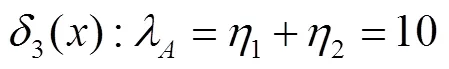
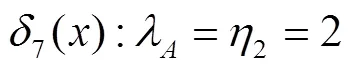
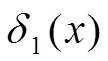
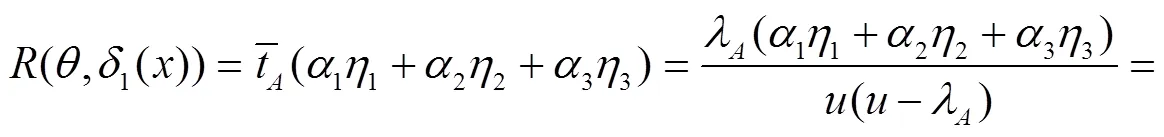
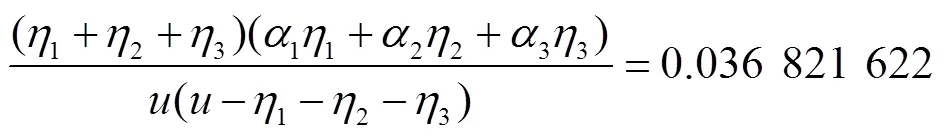
同理，可计算出其他7种决策函数对应的风险函数为：

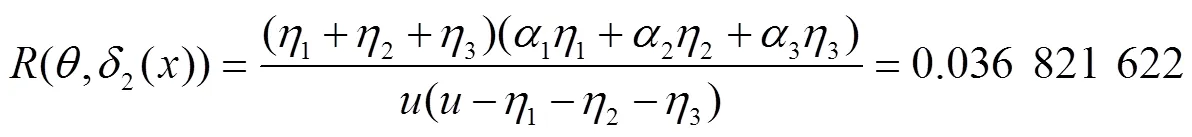
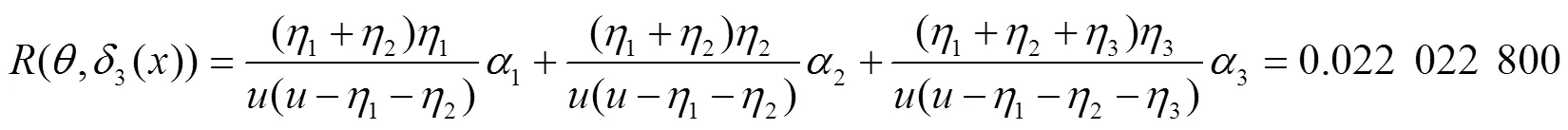
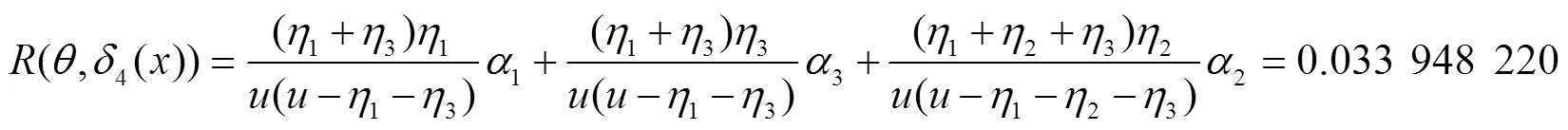
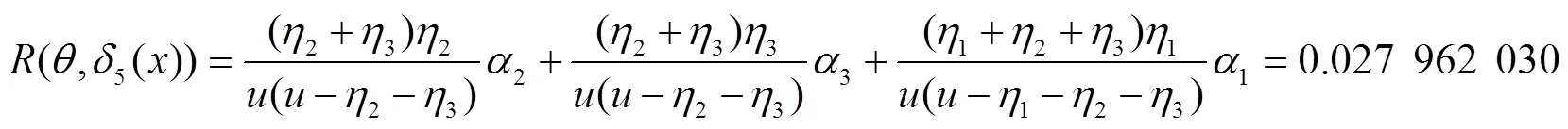
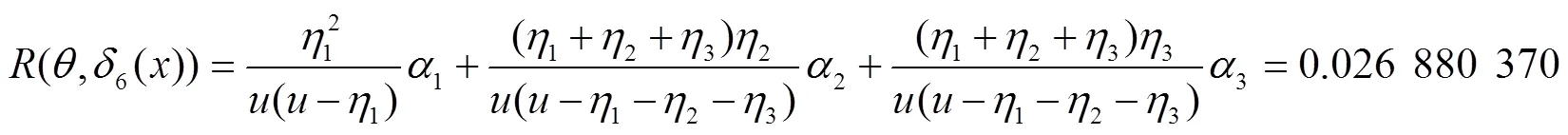
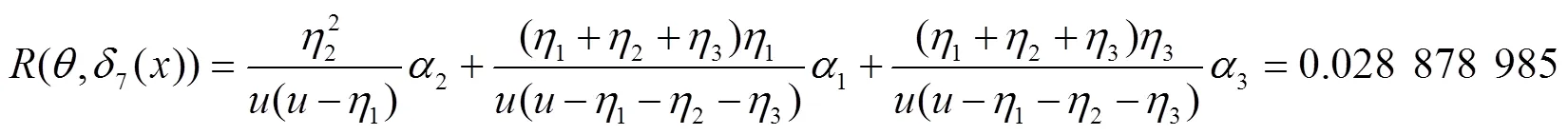
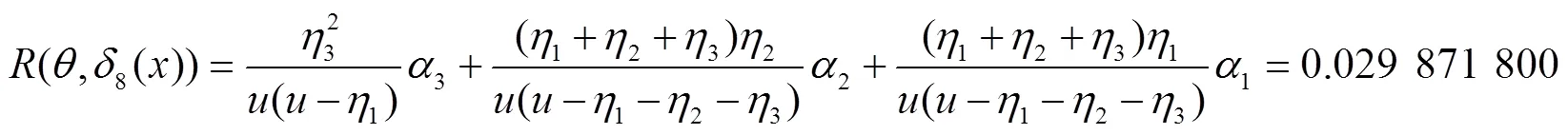
在该仿真系统中，各个决策行动对应的风险函数值如图2所示：

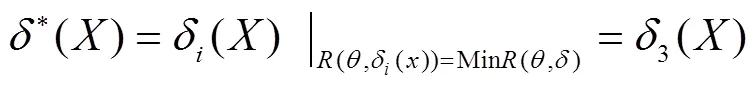
4 结论

本文提出了一种优先级决策优化方法，将统计决策及风险函数引入信息系统的优先级设定中，从而计算出在不同优先级行动决策下的系统损失期望，选择出最优的优先级处理方案，以降低模拟通信系统的运行风险. 该方法可扩展到其他应用场合信息控制系统的决策优化设计.

[1] 张柏生，任剑锋，孟相如. 基于排队论的网络通信系统的建模与分析[J]. 空军工程大学学报：自然科学版，2002(3): 59-62.

[2] 唐应辉，刘晓云. 延迟多重休假M~x/G/1排队系统的队长分布[J]. 系统工程学报，2004(6): 583-588.

[3] 陈春东. 数字排队调度系统的可靠性分析[J]. 电信快报，2012(6): 3-4.

[4] 余润仙，高爱乃，丁永生. RFID系统中反碰撞处理的排队建模与分析[J]. 计算机仿真，2005(8): 286-288.

[5] 金海波，仲崇权. 基于排队论的实时以太网缓存队列优化算法[J]. 大连理工大学学报，2012(1): 95-99.

[6] 唐应辉，唐小我. 排队论—基础与分析技术[M]. 北京：科学出版社，2006.

[7] 王梓坤. 随机过程[M]. 北京：科学出版社，1978.

[8]BERGER J O. Statistical decision theory and Bayesian analysis [M]. New York: Springer, 1985.

[责任编辑：韦 韬]

Optimizations of the Service Priority Strategy for M/M/1/∞/∞/PS Communication Systems

LIHua-song, LUOBing, YUJian-song

(School of Information Engineering, Wuyi University, Jiangmen 529020, China)

In this paper, the risk function is introduced into the priority decision-making of the M/M/1/∞/∞/PS information system and the uniformly minimum risk function is used to evaluate the loss expectation of decision-making in action spaces, thereby reducing the loss risk in the design of mass communication systems and ensuring the safety and rationality of long-term system operations.

system priority; message queue process; information priority strategy

1006-7302（2013）02-0048-06

TN911

A

2012-09-05

广东省自然科学基金博士启动项目（S2011040005275）

李华嵩（1975—），男，广东新会人，讲师，博士，研究方向为智能电网检测技术及自动化.