浅谈复变函数的可微性与解析性
2013-07-13高喜花
高喜花
(河南水利与环境职业学院,河南郑州450011)
浅谈复变函数的可微性与解析性
高喜花
(河南水利与环境职业学院,河南郑州450011)
本文主要介绍复变函数的可微性与解析性,并利用柯西-黎曼方程推出它们成立的充分条件、必要条件和充要条件,最后归纳总结出复变函数的可微性与解析性的联系与区别.
复变函数;可微性;解析性;解析函数;柯西-黎曼方程
在复变函数教学中,解析函数是复变函数论研究的主要对象,它是一种具有某种特性的可微函数.函数的解析性与可微性是一个学习重点,也是易混淆的学习难点.文章对这部分内容进行了思考总结,指出复变函数可微性与解析性的联系与区别,从而有利于更好地理解和掌握复变函数.
1 复变函数的可微性
1.1 复变函数可微性的定义
定义1.1设函数w=f(z)在点z0的邻域内(或含z0的区域D内)有定义,若极限
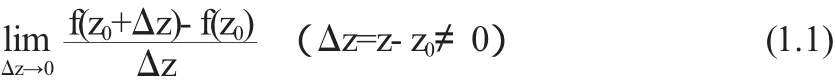
存在,则称此极限为函数f(z)在点z0的导数,记为f'(z0)这时也称f(z)在点z0可导.
定义1.2若函数w=f(z)在点z0可导,则称f'(z0)Δz为函数w=f(z)在点z0的微分,记为
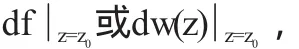
即

此时也称f(z)在点z0可微.
特别地,当f(z)=z时,dz=Δz,于是(1.2)变为
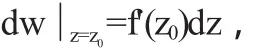
即
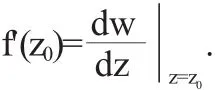
由此可见,在复变函数中f(z)在点z0可导与f(z)在点z0可微是等价的.
函数由f(z)在点z可导与可微的概念与数学分析中的可导与可微这两个概念相类似,因此数学分析中求导基本公式,均可类似地推广到复变函数中来.同时,与数学分析中一样,函数f(z)在点z可微,则f(z)在点z连续,反之不一定成立,但在数学分析中,要构造一个处处连续又处处不可微的例子是一件非常困难的事情,而在复变函数中,这样的例子却几乎是随手可得.如果函数f(z)在区域D内每一点都可微,则称f(z)在区域D内可微.
1.2 柯西-黎曼方程
设w=f(z)=u(x,y)+iv(x,y)下面我们来探讨f(z)的可微性与二元实函数u(x,y)及v(x,y)之间存在的关系.
若f(zz)=u(x,y)+iv(x,y)在点z=x+iy可微,且设

又设
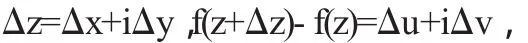
其中

则(1.3)变为

由于当Δz=Δx+iΔy不论按什么方向趋于零时,(1.4)式总是成立,因此我们可以先设Δy=0,Δx→0,即点z+Δz沿着平行于实轴的方向趋于点z(图1),
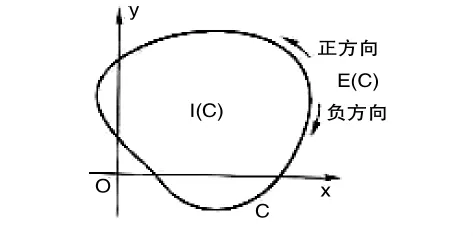
图1
则此时(1.4)变为
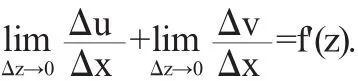
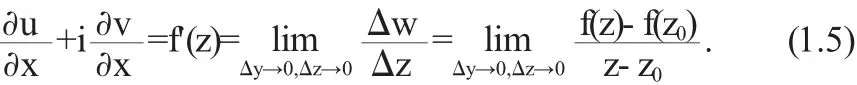
同理,设Δx=0,Δy→0,即点z+Δz沿着平于虚轴的方向趋于点z(图1),此时(1.4)变为
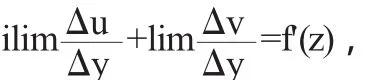

由(1.5),(1.6)及复数相等性质可得

则(1.7)称为柯西-黎曼条件或柯西-黎曼方程,简称为方程.
总结上述讨论,即得:
1.3 复变函数可微性的必要条件
设函数f(z)=u(x,y)+iv(x,y)在区域D内有定义,且在D内一点z=x+iy可微,则有
(1)在点(x,y)处偏导数ux,uy,vx,vy都存在;
(2)u(x,y),v(x,y)在点(x,y)满足C-R方程.
但它的逆命题不成立.
1.4 复变函数可微性的充分条件
设f(z)=u(x,y)+iv(x,y)在区域D内有定义,且f(z)在D内一点z=x+iy可微的充分条件是:
(1)偏导数ux,uy,vx,vy在点(x,y)处连续;
(2)u(x,y),v(x,y)在点(x,y)满足C-R方程.
1.5 复变函数可微性的充要条件
设f(z)=u(x,y)+iv(x,y)在区域D内有定义,则f(z)在D内一点z=x+iy可微的充要条件是:
(1)u(x,y),v(x,y)在点(x,y)可微;
(2)u(x,y),v(x,y)在点(x,y)满足C-R方程.
当上述条件满足时,有
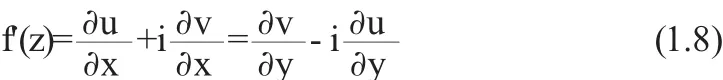
例1证明函数f(z)=■|xy|在z=0有定义,但在z=0不可微.
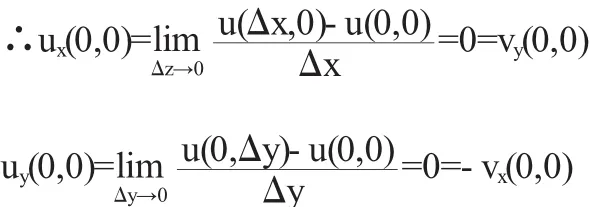
但是由于

因此当Δz沿着射线Δy=kΔx(Δx>0)随着Δx→0时,
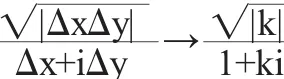
它是一个与k有关的值,故不存在,即f(z)在z=0不可微.
2 复变函数的解析性
2.1 复变函数解析性的定义
若函数w=f(z)在区域D内可微,则称f(z)为区域D内的解析函数(或全纯函数、正则函数).此时也称f(z)在区域D内解析.
解析函数是复变函数论研究的主要对象,它与相伴区域密切相关.以后说到f(z)在某点解析.则表示f(z)在该点的某一邻域内解析,说f(z)在闭域D上解析,则表示f(z)在包含D的某个区域内解析.因而解析的概念要比可微的概念条件要强得多.
2.2 解析函数及其简单性质
与数学分析一样,解析函数也有如下基本性质:
(1)若f1(z),f2(z)在区域D内解析,则其和、差、积、商(在商的情形,要求分母在D内不为零)也在D内解析,且
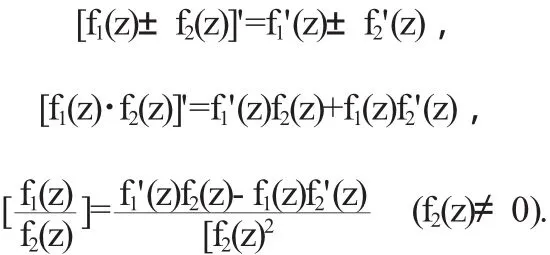
(2)(复合函数求导法则)设ξ=f(z)在区域D内解析,w=g (ξ)在区域G内解析,若∀z∈D均有ξ=f(z)∈G,则w=g[f(ξ)]在D内解析,且
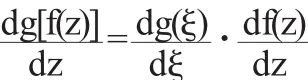
2.3 复变函数解析性的充要条件
函数f(z)=u(x,y)+iv(x,y)在区域D内解析的充要条件是:
(1)二元函数u(x,y),v(x,y)在区域D内可微;
(2)u(x,y),v(x,y)在区域D内满足C-R方程.
2.4 复变函数解析性的充分条件
函数f(z)=u(x,y)+iv(x,y)在区域D内解析的充分条件是:
(1)ux,uy,vx,vy在区域D内连续;
(2)u(x,y),v(x,y)在区域D内满足C-R方程.
例2试证f(z)=ex(cosy+isiny)在z平面上处处解析,且f' (z)=f(z)
证明由已知u(x,y)=excosy,v(x,y)=exsiny可分别求它们的偏导数得
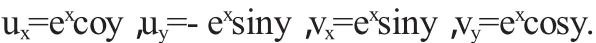
则满足C-R方程.所以u(x,y),v(x,y)在z平面上处处可微,故由解析的充要条件f(z)在z平面上处处解析.且由公式(1.8)可得
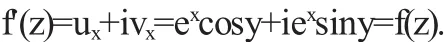
3 复变函数的可微性与解析性的区别与联系
通过上述关于复变函数可微性与解析性的概念及它们成立的条件我们可以总结出它们之间的联系:
(1)复变函数的解析性与可微性都满足C-R方程;
(2)函数的可微性是函数解析的前提.
同时,它们之间还存在着区别:
(1)函数的可微性定义域可以是点也可以是区域,而函数的解析性定义域是只能是区域.
(2)函数f(z)在一点解析是针对一个局部邻域,而函数在一点可微是对一个点而言.
所以可以总结出以下几点是成立的:
(1)w=f(z)在点z0处可导(可微),但不一定在z0处是解析的,
(2)f(z)在区域D内可微与在区域D内解析是等价的,
(3)函数f(z)在一点解析,则函数在该点一定可微.
例3函数f(z)=sinxchy+icosxshy何处可微?何处解析?
解由f(z)=sinxchy+icosxshy
设u(x,y)=sinxchy,v(x,y)=cosxshy可得它们对x和y的偏导数为
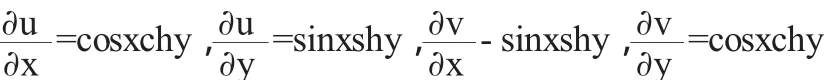
所以,函数在z平面上处处连续,且在整个复平面满足C-R方程,故
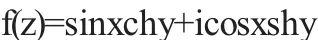
在z平面上处处可微,在z平面上处处不解析.
〔1〕钟玉泉.复变函数(第三版)[M].北京:高等教育出版社,2004.
〔2〕钟玉泉.复变函数学习指导书[M].北京:高等教育出版社,2003.
〔3〕余家荣.复变函数(第三版)[M].北京:高等教育出版社,2000.
〔4〕龚东宝.复变函数典型题解[M].西安:西安交通大学出版社,2002.
〔5〕路可见,等.复变函数[M].武汉:武汉大学出版社,2004.
〔6〕方企勤.复变函数教程[M].北京:北京大学出版社,1996.
O174
A
1673-260X(2013)08-0008-03
