基于映射函数收缩算法的图像去噪方法
2013-07-13李会方王正民
吴 军,李会方,王正民
(1.西北工业大学 陕西 西安 710129;2.中国兵器工业第203研究所 陕西 西安 710065)
图像是人们获取信息的一种极为重要的信息源之一,在拍摄、采样、量化、保存以及传输图像的过程中,不可避兔地受到噪声干扰,导致转换后得到的数字图像质量下降,给图像处理和分析带来不必要影响,极大地妨碍了人们对图像内容的理解[1]。因此在对图像进行分析之前,必须进行去噪预处理,以改善图像质量并尽可能地保留图像信息特征。使得图像更加真实地再现目标场景。但是如何兼顾降低噪声和保留细节仍然是一个难题[2]。
图像噪声按其来源可分为加性噪声、乘性噪声、量化噪声、椒盐噪声等类型,实际图像数据中所含噪声是各种噪声的混合。长期以来,人们根据图像的特点以及噪声的统计特征和频谱分布的规律,提出了许多去噪方法。中值滤波、空域滤波器、维纳滤波以及变换域去噪等都是非常有效的去噪方法,它们对不同的噪声有不同的去噪能力。中值滤波能有效地抑制脉冲和椒盐噪声,但它对于图像中高斯噪声的去除效果不佳。空域滤波器作为一种传统方法具有适应范围广、速度快、运算代价低等特点,但模糊了图像边缘和纹理等细节信息。维纳滤波对高斯噪声和乘性噪声都有较好的抑制作用,但缺点是仍然是容易失去图像的边缘信息[3]。小波去噪是变换域去噪的典型方法,其基本方法是对含噪图像进行多尺度小波变换,通过选择合理阈值,在各尺度下尽可能提取有用图像的小波系数,去除属于噪声的小波系数,再用小波逆变换重构图像。但硬阈值滤波容易在图像的边缘处产生突变,而软阈值收缩函数有时会使图像过于平滑的问题[4-6]。
近年来,稀疏表示己成为一个新的研究热点。它在与信号结构匹配方面具有很好的灵活性,并具有超分辨、去除噪声和表达信号灵活等优点,在谱估计、信号分析、目标特征提取、图像压缩等方面得到了广泛的应用[7]。本文结合小波变换和稀疏表示方法,提出一种基于图像稀疏性与冗余表达模型的映射函数收缩去噪方法。将图像有用信息部分作为图像中稀疏成分,而将图像中的噪声作为图像(去除其中稀疏成分后得到)残差,以此作为图像去噪处理的基础。相对于传统的去噪算法,去除噪声效果更为理想。
1 映射函数收缩算法
噪声图像的形成模型可表示为:

其中x为原图像,n为噪声模型,y为带噪声图像。对式(1)两边进行小波变换:

式中Cy、Cx、Cn分别表示观测图像y原始图像x和噪声n的小波变换,则

由式(3)可以看出,如果知道噪声小波变换Cn,那么就可以很轻松得由Cy得到Cx,并求得原始信号x。但是很明显,对于去噪Cn的求解是个很复杂的问题。
为了简化模型,将观测信号与原始信号之间的变换过程用一个映射函数(Map Functions)M{·}来描述[8-9]:

式(4)表示观测信号通过某种变换M{·},得到了不含噪声的原始信号。
1.1 问题规划
由前面的分析可知,图像的去噪过程可用一个映射函数描述,为了简化对这个映射函数的学习过程,可以将这个映射函数分解为一组多尺度的映射函数 (MFs:Map Functions){Mk,k=1, …,K},Mk为小波子带系数,K 是小波分解的子带数。对于信号y,其小波变换为:

式中,W=[B1,…,BK]T为小波变换函数,Bk(k=1,…,K)为小波子带变换。 其 α=[α1,…,αK]为小波变换系数,αk(k=1,…,K)为其对应Bk的小波变换系数。由式(5)可得,映射函数为:
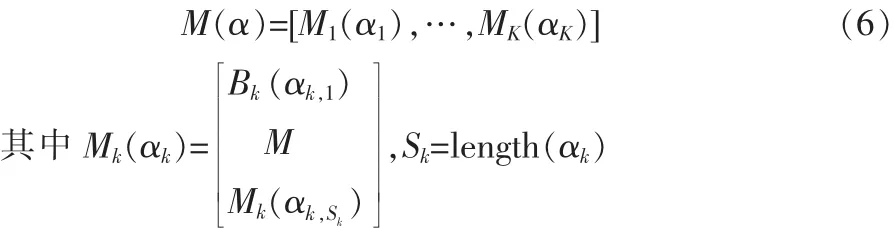
简而言之,这个映射变换M{·}被划分成了K个映射函数,K由小波变换的子带个数来决定。
由此可见,图像去噪问题久转换为一个寻找变换M{·}过程,将这个变换作用于观测图像,可以使观测图像尽可能的逼近于不含噪声的原始图像,也就是完成了去噪的过程。其数学模型可以表示为:

由式(8)将图像去噪问题转换成了求最优值的问题。
1.2 算法求解
对于(8)提出的最优化问题,可以使用切片变换(Slice Transform,SLT)来解决这个问题。切片变换可将一个非线性的问题转化为一个分段线性问题。通过SLT可将(8)式变换为:
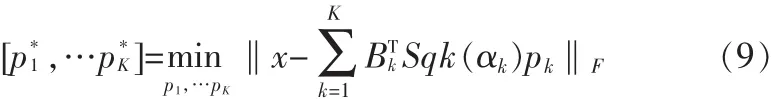
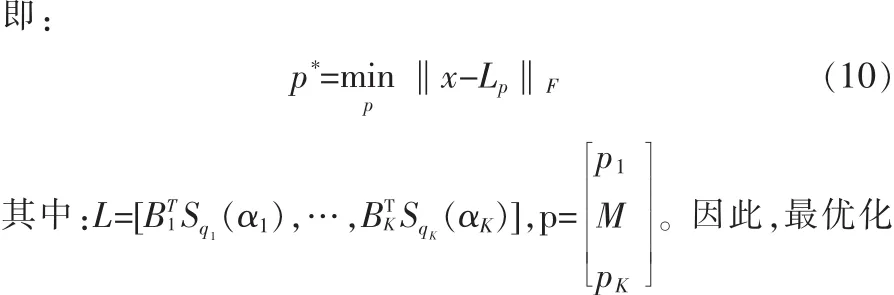
问题转换成了经典的最小方差问题,其解为:

整个算法流程如下:
1)对观测图像进行小波变换,获得K个小波子带系数:α1,…,αK;
2)用 Lloyd-Max 算法,确定 M+1 维向量 qk;k=1,…,K
3)对于每个子带:
①计算 SLT 矩阵 Ck=Sqk(αk),Ck∈RNk×(M+1),Nk=length(αk);
②将每个 Ck拉直为 Ck(:,m),m=1,…,M+1。 求其逆:

4)将 zk,m按列排列,组合成 n×K(M+1)维矩阵 L;
5)通过式(9)求出 p*。 这是一个 K(M+1)维的向量,将其划分为 K 个向量,p*1,…,p*K,每个子向量为(M+1)维。
这样就完成了对映射函数的学习问题。
1.3 图像去噪
不同于小波收缩算法,MFs算法更偏向于稀疏表示的去噪算法,主要工作在于学习字典。MFs算法则是学习一个变换函数,变换函数学习出来去噪过程就变得很简单了。具体去噪步骤如下:
1)对于训练样本,使用1.2中算法,求得变换函数M;
2)由式(5)可知,求解 WT[M(Wy)]即为去噪后图像,其中W为小波变换,y为测试样本。
2 实 验
本文分3个实验分别验证MFs算法的可行性,与其他算法对比的优越性和自身算法的鲁棒性。实验训练样本均为加入噪声强度λ=20的高斯噪声的Lena512×512灰度图像。
2.1 验证可行性
使用测试样本为Lena256×256的灰度图像,加入噪声强度λ=20的高斯噪声。实验结果如图1所示。
容易看出,经过MFs算法去噪后,图像的轮廓和较明显的细节都被保留下来,直观上有效地去除了图像噪声。
2.2 对比经典小波去噪,经典稀疏表示去噪和MFs去噪算法
为了进一步说明本文所提出算法的有效性,采用峰值信噪比(peak signal noise ratio,PSNR)和均方误差(mean square error,MSE)作为评价指标。设输入测试图像为Lena灰度图像,大小为512×512像素,人为加入λ=20的高斯噪声,小波去噪采用文献[9]中方法,SRC方法采用文献[10]中方法,对比几种方法所得输出信号均方误差和峰值信噪比如表1所示。

图1 加噪图像和去噪后图像对比Fig.1 Noisy image compared with denoised image
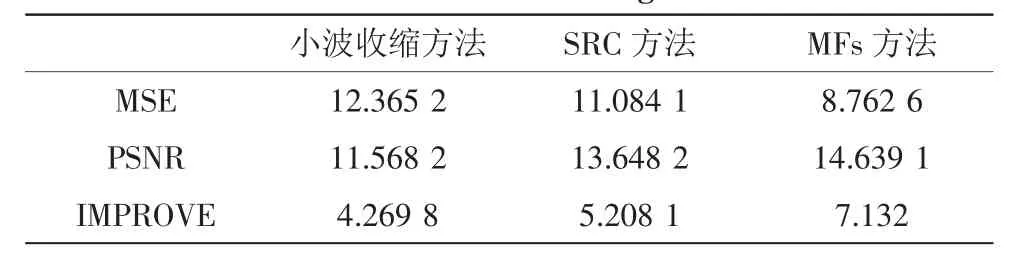
表1 3种方法的去噪结果对比Tab.1 Three methods of denoising results contrast
其中IMPROVE表示去噪后图像性噪比的提高。由表1可以看出,本文算法与前面两种算法相比较,均方误差(MSE)较小,峰值性噪比(PSNR)最大,且性噪比提高最多。说明本文算法具有较优越的去噪性能。
2.3 当改变噪声强度时,本文算法的鲁棒性测试
为了验证算法在不同噪声强度下的鲁棒性,分别对测试图像加入λ=10、λ=20、λ=30的高斯噪声,实验结果如表2所示。

表2 不同噪声强度下的去噪结果对比Tab.2 Denoising results compared under different noise intensity
表2显示,随着所加入噪声强度的增加,去噪后图像的峰值性噪比(PSNR)有所下降,但是下降趋势较缓,当加入噪声强度λ=30的高斯噪声时,峰值性噪比仍与表1中用SRC方法对噪声强度λ=20的图像进行去噪后的结果相当,可见本文算法具有一定的鲁棒性。
3 结束语
可以看出,本文算法是一种鲁棒性较强的图像去噪方法,且对于同种噪声,去噪效果好于小波方法和SRC方法,最大的优点在于映射函数的提出,摆脱的求解最大后验概率的困境,只需要对学习样本进行学习就可以应用到测试样本之中,但是当测试样本的复杂性高于学习样本时,本文算法的效果往往较差,所以学习样本的选择问题依然是一个值得探讨的问题。
[1]郭德全,杨红雨,刘东权,等.基于稀疏性的图像去噪综述[J].计算机应用研究,2012,29(2):406-413.
GUO De-quan,YANG Hong-yu,LIU Dong-quan,etal.Qverview on sparse image denoising[J].Application Research of Computers,2012,29(2);144-145.
[2]张德丰.MATLAB数字图像处理[M].2版.北京:机械工业出版社,2012.
[3]乔闹生.一种混合噪声图像去噪方法[J].计算机工程与应用,2009,45(29):144-145.
QIAO Nao-sheng.Denoisingmethod in mixturenoise image[J].Computer Engineering and Applications,2009,45(29);144-145.
[4]李骜,李一兵,孟霆,等.基于小波阈值去噪的收缩函数改进方法[J].计算机工程与设计,2011,32(10);3450-3452
LI Ao,LI Yi-bing,MENG Ting,et al.Improved method of shrink-function based on wavelet threshold de-noising[J].Computer Engineering and Design,2011,32(10);3450-3452.
[5]林清馨,吕祚坤,梁潇.基于小波收缩的噪声图像恢复新型算法实现与验证[J].电子设计工程,2011(24):158-160.
LIN Qing-xin,LV Zuo-kun,LIANG Xiao.Noise based on waveletshrinkage algorithm forimage restoration and verification[J].Electronic Design Engineering,2011(24):158-160.
[6]胡静波.基于小波变换与改进中值滤波的红外图像去噪[J].现代电子技术,2011(18):50-52.
HU Jing-bo.Infrared image de-noising based on wavelet transform and improved median filtering[J].Modern Electronics Technique,2011(18):50-52.
[7]尚丽,郑春厚.基于稀疏编码的自然图像特征提取及去噪[J].系统仿真学报,2005,17(7):1782-1784.
SHANG Li,ZHENG Chun-hou.Image feature extraction and denoising based on sparse coding[J].Journal of System Simulation,2005,17(7):1782-1784.
[8]Hel-Or Y,Shaked D.A discriminative approach for wavelet denoising, IEEE, IP,2008(17):443-457.
[9]Adler A,Hel-Or Y,Elad M.A shrinkage learning approach for single image supervresolution with over-complete representations[C]//Computer Vision, ECCV(2010), Springer
[10]HE Yan-lan,SU Yong,GAO Yong-mei.Adaptive wavelet denoising algorithm[J].Tien Tzu Hsueh Pao/Acta Electronica Sinica,2000,28(10):138-140.
