一致有界原理的另一种证法

牛潇萌

（赤峰学院数学与统计学院，内蒙古赤峰024000）

一致有界原理的另一种证法

牛潇萌

（赤峰学院数学与统计学院，内蒙古赤峰024000）

本文用反证法给出一致有界原理的一个没有利用Baire纲定理任何其他形式去推导的证明.

赋范空间；一致有界原理；反证法

Banach空间是泛函分析中最基本，最重要的空间，它对泛函分析的意义，恰如Euclid空间对于数学分析的意义.一致有界原理是Banach空间中的一个重要定理，例如它在许多分析问题的研究涉及有界线性算子列的收敛性或一致有界问题上起重要作用.

1 已有证明方法

一般来说，在泛函分析教材中，一致有界原理是直接从Baire纲定理推导出来的.在文献[1]中利用Zabreǐko引理给出了一致有界原理的又一种证明方法.

定义1[1]向量空间X上的半范数或准范数是X上的一个实值函数p，使得对X的所有元素x和y以及每一个纯量都满足下列条件∶

(1)p(αx)=|a|p(x)；

(2)p(x+y)≤p(x)+p(y)；

定义2[1]从赋范空间X到非负实数集中的函数f，称为是可数次可加的，如果对X中的每一个收敛级数∑nxn，有

定理1[1](Zabreǐko引理)Banach空间上的每一个可数次可加的半范数都是连续的.

下面利用Zabreǐko引理给出了一致有界原理的证明.

定理2[1]（一致有界原理）假设X是Banach空间，Y是赋范空间.Ψ={T∶T∈B(X,Y)}满足条件

证明对每个x∈X，令p(x)=sup{||Tx||∶T∈Ψ}，并假设p是有限值的.

下面证明p就是X上的一个可数次可加的半范数.

显然，对每一个x∈X和每一个α∈F，有p(αx)=|α|p(x).

2 反证法证明一致有界原理

一致有界原理假设X是Banach空间，Y是赋范空间. Ψ={T∶T∈B(X,Y)}满足条件

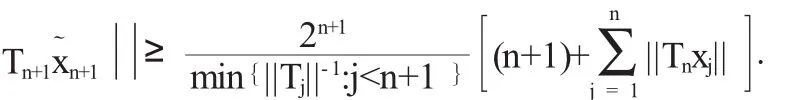
对于上述的xn有是有限数.由于Banach空间中绝对收敛级数是收敛的，因此则x就是所要找的.这是因为，

〔1〕Robert E.Megginson,An Introduction to Banach Space Theory[M].1998.Springer-Verlag,New york，41：47,49：58.

〔2〕刘炳初.泛函分析[M].北京：科学出版社,2007.

〔3〕刘培徳.泛函分析基础[M].武汉：武汉大学出版社,2001.

〔4〕罗跃生，杜维华.简明泛函分析[M].哈尔滨：哈尔滨工程大学出版社,2002.

O177

A

1673-260X（2013）01-0010-02