导热反问题在身管传热中的应用

陈 刚，周渊键，吴 斌

(解放军陆军军官学院 a.机械工程教研室;b.研究生管理大队1 队;c.装甲兵系，合肥 230031)

导热反问题是相对导热正问题而言的一个交叉学科，它涉及传热学、物理学、数学、计算机、实验技术等众多的领域，在实际工程中有着广泛的应用前景［1-5］。

导热反问题在各领域中有着广泛的应用背景，但其非适定性、非线性、计算量大等特点，使得求解比较困难［6-8］。导热反问题作为一个优化问题，已有一些求解方法，如基于梯度的优化方法Levenberg-Marquardt 算法、遗传算法、贝叶斯方法等［9-11］。

文中以对火炮发射时内膛热交换过程的分析，基于导热反问题的研究方法，根据Levenberg-Marquardt 算法建立由结构内部一个或多个温度测点的测量值计算内膛壁温度与热流密度的数学模型。

1 导热正问题

模拟三维水平火炮身管物理模型如图1 所示，内径为50 mm，外径70 mm，长200 mm。本文中假设xoy 面为对称面，水平身管上下热工情况相同，因此只取水平身管的一侧进行讨论。水平身管的内外壁分别为第一类与第三类边界条件，其控制方程及边界条件为:

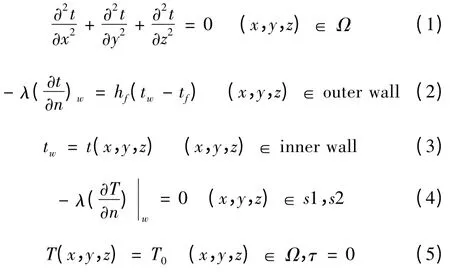
本文使用有限单元法求解导热问题，采用八节点六面体等参单元离散模型，如图1 所示。在内壁边界条件及身管导热系数已知情况下，求解导热正问题，获得身管内壁温度场。式(1)～式(5)构成三维火炮身管瞬态导热初边值定解问题。已知内外壁边界条件及初始温度，即可计算出身管随时间变化的温度分布。

图1 网格模型

2 导热反问题

在求解导热正问题时，内外壁边界条件已知，需要求解的未知量为外壁面的温度;而在进行反问题分析时，内壁面的温度分布为未知参量，需要根据外壁面的测量温度，利用反演算法求得。

本文待反演的参量为身管内壁面的温度分布，属于函数估计问题。Su 等借鉴有限单元法中单元形函数的思想，把反问题中的函数估计转化为参数估计问题。本文亦用此法，把内壁温度场的反演转化为内壁有限结点温度的反演。

在水平身管内壁面的轴向方向，温度值为

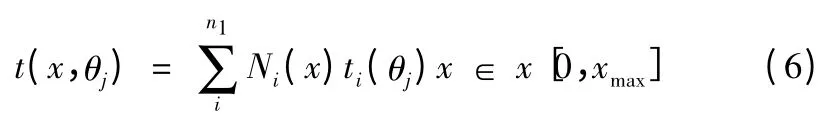
式中:t(x，θj)为在横坐标为x 的横截面上ti(θj)为身管内壁面圆周方向上θj角处的温度值，为已知值，在反问题分析中为待反演参量;Ni(x)为身管内壁轴向上的形函数，本文算例中采用线性插值函数，类似地，在水平身管内壁面圆周方向，温度值由式(7)确定

本文研制的是一种无机泡沫吸波材料，是利用碎玻璃或火山灰等为主要原材料，在其中添加电磁损耗物质，熔融发泡而成的一种隐身材料，如图7所示。

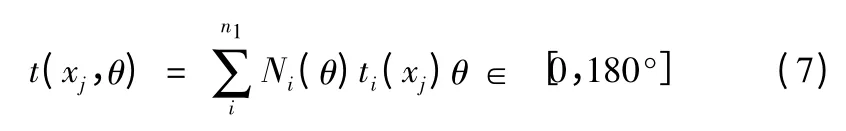
式中:t(xj，θ)为横坐标为xj的横截面是θ 角处的温度值，θ为变量;ti(xj)为管内壁横坐标为xj的横截面上的温度值，为已知值，在反问题分析中为待反演参量;Ni(θ)为身管内壁圆周上的形函数，本文算例采用线性插值函数。

利用式(6)和式(7)，反问题由函数估计问题转化为参数估计问题。为了构建导热反问题的目标函数，先把未知参量表示为向量形式

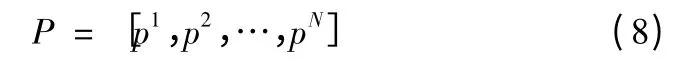
式中:pi表示内壁面选定点处的温度;N 为选定待反演未知参量的总数。

构建反问题目标函数

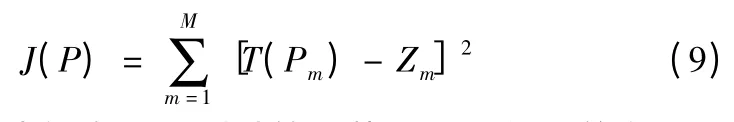
式中:T(Pm)为未知向量P 时计算导热正问题得到的在测量点处的温度值;Zm为测量温度值;m = 1，2，…，M，M 为测点总数。

式(9)可写为

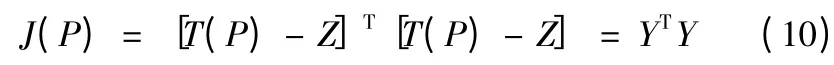
式中:Y 为测量点计算温度值与测量温度值的向量差，且Ym=Tm-Zm。由此，导热反问题即可视为一个优化问题，即利用一定的反演算法，构造出内壁边界条件，以使目标函数J(P)达到最小。

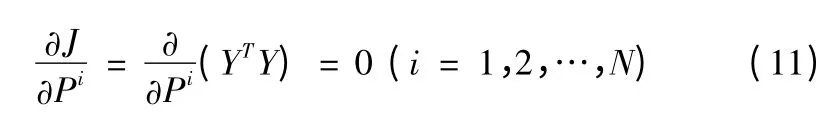
对Y(P)进行Tayor 展开，并省去二阶以上高阶项，代人式(11)并整理成迭代式得

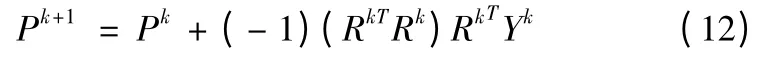
式中:R 为Jacobian 矩阵。

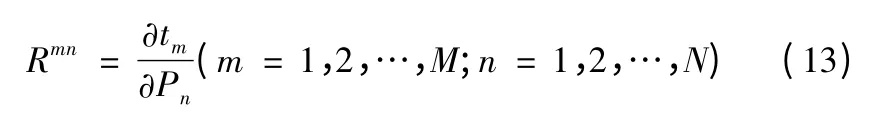
引入修正系数a 调节收敛速度，得Levenberg-Marquar 算法迭代式

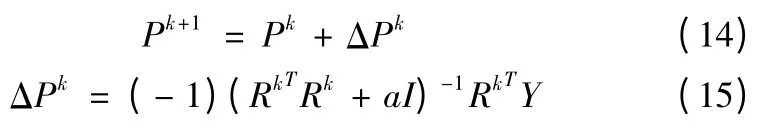
式中，I 为(n+1)阶单位矩阵。

通过不断地计算正问题，由式(14)求得新的反演参量，直到未知参量值P 满足迭代终止条件式(16)

式中:ε 为较小的正数，如1 ×10-6。

3 试验验证

针对前面提出的问题，以直角坐标系为例，通过计算钢-耐火纤维-钢三层材料组成结构的外表面温度、热流密度来验证上述数学计算模型的正确性。试件结构及尺寸如图2所示，试件总厚度为80 mm，外壳是厚度为15 mm 的不锈钢元件，内壳不锈钢元件厚度为15 mm，中间层为隔热缓冲层，厚度为50 mm。

假设在距外壁面5 mm，10 mm，25 mm 处各布置有一对热电偶测温点，分别命名为1#，2#，3#测温点。为了计算方便，其初始条件假设为室温25 ℃，已知边界条件假设为绝热边界。通过三角波形热流变化模拟和验证导热反问题在外壁热流在该变化情况下的反演计算，并考察测温点位置、数目及时间步长对计算结果误差的影响。

首先假设真实热流变化变化曲线如图2 所示，以图2 中三角波形热流作为初始条件，通过计算导热正问题方程可得到结构内部温度场，其中外壁面温度变化曲线如图3 所示;然后取3 个测温点所在位置的温度变化历程作为反问题计算输入条件，可以得到反问题计算热流及外壁面温度变化曲线如图4 和图5。

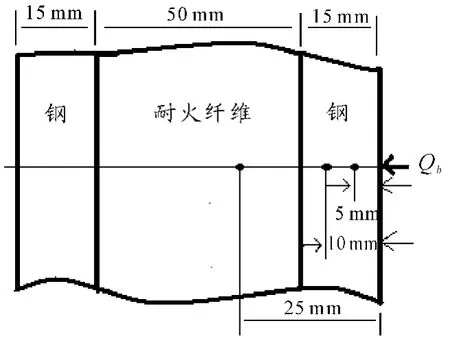
图2 组合结构和热电偶分布

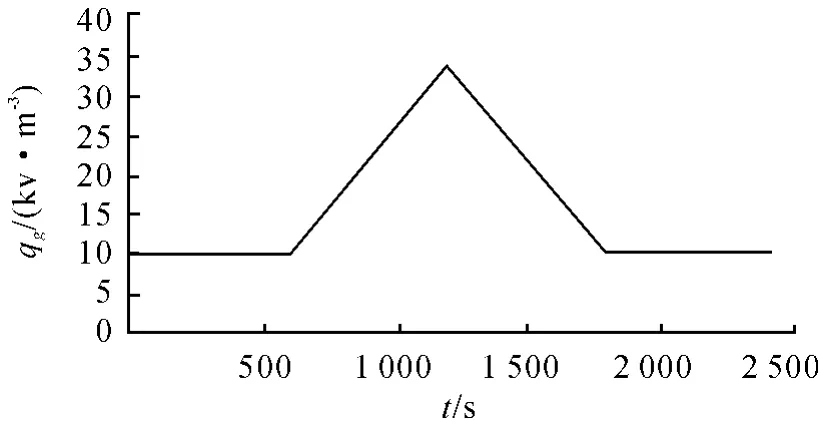
图3 实际热流变化曲线

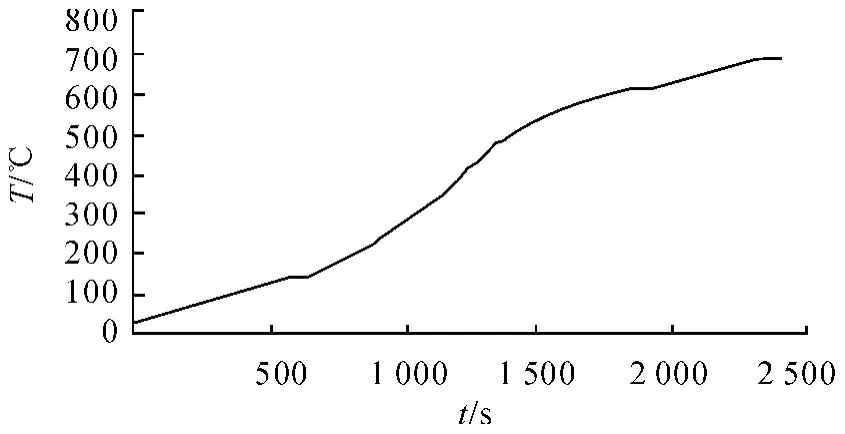
图4 正问题计算外壁面温度曲线

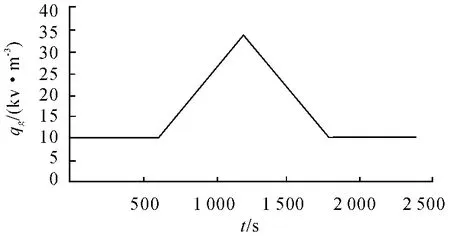
图5 反演热流变化曲线

从图2 ～5 可以看出，利用正问题计算得到的内部测温点温度值，作为导热反问题输入条件的导热反问题方法，对于三角波形变化热流(也即缓变热流)情况下的计算，无论是外壁热流值还是外壁面温度值都符合较好。

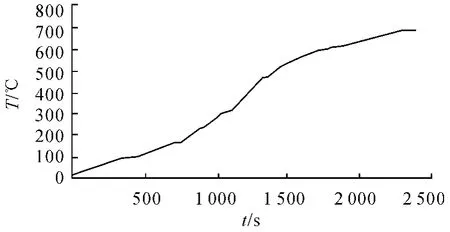
图6 反问题计算外壁面温度曲线

4 结束语

本文所讨论的导热反问题方法，适用于对航天器、火炮身管、核电及化工等大型工程设备进行瞬态传热研究时计算介质对容器内壁的放热系数，该方法不需要布置热电偶和热流密度计，而仅需要在容器外壁或内壁布置热电偶，大大简化了试验难度。通过计算模拟钢-耐火纤维-钢三层材料组成结构的外表面温度、热流密度来验证上述数学计算模型的正确性。

［1］薛齐文，杨海天.应用共轭梯度法求解非线性多宗量稳态热传导反问题［J］.计算力学学报，2005(22):51-54.

［2］陶文铨.传热学［M］.西安:西安工业大学出版社，2006:78-103.

［3］吴斌，夏伟，汤勇，等.射击过程中热影响及身管热控制措施综述［J］.兵工学报，2003，24(4):525-529.

［4］Beck J V，Blackwell B，St C R.clair inverse heat conduction-Ill posed problems［M］. New York: Wiley - Interscience，1985(1):218-243.

［5］Beck J V.Methodology for comparison of inverse heat conduction methods［J］. J. of heat transfer，1988( 110): 30-37.

［6］Lawton B. Thermal-chemical erosion in gun barrels［J］.Wear，2001(251):827-838.

［7］杨冬，陈听宽.导热反问题方法在瞬态传热过程中的应用［J］.核动力工程，1997，18(6):553-558.

［8］李明海.钢-木组合结构的火烧热响应模拟与导热反问题在火烧试验中的应用［D］.重庆:重庆大学，1998:42-60.

［9］薛齐文，杨海天.应用共轭梯度法求解非线性多宗量稳态热传导反问题［J］.计算力学学报，2005(22):51-54.

［10］杨海天，薛齐文.两级敏度分析求解非线性稳态多宗量热传导反问题［J］. 工程热物理学报，2003，24(3):463-465.

［11］王靖君，赫信鹏. 火炮概论［M］. 北京: 兵器工业出版社，1997.

［12］赵金辉，何忠波，傅建平，等.火炮发射过程中身管温度场及弯曲度的有限元计算［J］. 火力与指挥控制，2011(5):106-109.