稳健的变量选择方法及其应用
2013-07-07樊亚莉徐群芳
樊亚莉, 徐群芳
(1.上海理工大学理学院,上海 200093;2.浙江农林大学理学院,临安311300)
稳健的变量选择方法及其应用
樊亚莉1, 徐群芳2
(1.上海理工大学理学院,上海 200093;2.浙江农林大学理学院,临安311300)
在已有的变量选择方法和稳健估计方法的基础上,提出了一种针对纵向数据的稳健的变量选择方法,通过模拟衡量其稳健性,并将其应用到一组实际的纵向数据分析中.模拟和实例分析结果表明,提出的稳健的变量选择方法在选择变量、估计变量系数的同时,对数据中可能存在的异常值有明显的抵抗作用.
惩罚函数;估计方程;稳健性;变量选择
统计学的中心任务是对观测到的因变量和自变量进行建模,从而对因变量在未来的取值进行预测和一些统计推断.在现实问题的数据中往往会含有多个自变量,如果建立的模型中含有多余的自变量,不仅会引起过度拟合,还会影响估计的精度和估计的效率[1].因此,如何选择出真正对因变量有影响的自变量是建模过程中值得关注的问题.另一方面,如果数据中存在异常值,这些个别的异常值也会对模型中参数的估计造成很大的影响[2].
针对上述两个问题,统计学家们作了大量的研究.一方面,对于变量选择问题,统计学方法已经由古典的子集选择方法发展到近年来的系数压缩方法[3].文献[4]提出的带有光滑截断绝对差的惩罚似然方法(SCAD)能够将变量选择和对回归系数的估计同时进行,这大大缩减了传统的AIC(Akaikes infotmation critetion)、BIC(Bayesian informationcriterion)等方法的计算量和计算时间.另外,文献[5]提出的最小绝对压缩选择算子方法(LASSO)和文献[6]提出的硬截断惩罚方法(Hard),以及之后文献[7]提出的弹性网方法(EN)和文献[8]的自适应的LASSO方法(ALASSO)都属于同一类型的变量选择方法.这些方法的共同点是将一个损失函数(如最小二乘损失、似然函数、估计方程等)加上一个惩罚项,作为新的目标函数加以优化.它们的区别在于所加的惩罚函数各有不同[9].另一方面,在稳健性问题上,许多学者研究了异常点对估计的影响以及对异常点的诊断[2,10].文献[11-12]等对稳健的估计方法进行了研究.
本文将上述两方面的工作结合起来,提出了一个稳健的变量选择方法,具体来说就是首先对估计方程稳健化,用一个依赖于自变量的权重函数使得杠杆点对估计方程的影响降低,并且对残差项使用一个有界的得分函数来限制因变量中异常点的影响;然后在稳健化的估计方程中加上一个连续的惩罚函数项,将稳健估计和变量选择同步进行.同样考虑将变量选择方法稳健化的研究还有文献[13-14].文献[13]是基于稳健化的拟似然方程建立一系列检验统计量来进行变量选择,文献[14]是基于一个加权二次预测风险函数将传统的Mallows的Cp准则(期望在p附近的准则)加以推广来进行变量选择.但是,这些工作都需要利用蒙特卡洛模拟来估计所拟合的模型的自由度,计算量比较大.本文的方法综合了稳健估计方程和系数压缩方法的优点,计算方便.模拟效果和实际应用效果显示,本文方法能在变量选择和估计的同时有效抵抗数据中异常点的影响.
1 稳健的惩罚估计方程

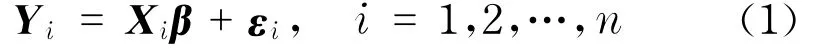
式中,Yi=(yi1,…,yimi)T;Xi=(xi1,…,ximi)T;β是d维回归系数向量;εi=(εi1,…,εimi)T表示随机误差向量.假设εij的期望为0,方差为σ2.假设不同个体之间的观测是相互独立的.
受文献[11]中稳健估计方法的启发,考虑稳健的估计方程

式中,Ri(α)为工作相关阵,它依赖一个未知参数α.常见的工作相关阵包括等相关、一阶自回归相关等[13,15].函数ψ(·)是一个有界得分函数,用来限制因变量中异常点的影响,本文选取Huber型函数ψc(x)=min{c,max{-c,x}},这里c是一个平衡稳健性和效率之间的调节参数.c越大,估计的效率越高,估计的稳健性就越差;相反,c越小,估计的稳健性越好,但效率越低.权重矩阵Wi=diag(wi1,…,wimi)用来降低自变量中杠杆点的影响.这里,类似于文献[12],使用如下定义的权重


如果取ψ(x)=x,wij=1,则式(2)退化为普通的估计方程.文献[11-12]主要考虑了模型参数的稳健估计方法,并没有考虑变量选择问题.
为了使变量选择和估计能同时进行,现考虑惩罚估计方程

现考虑几种近年来常用的一些惩罚函数.第1种是LASSO惩罚函数[5],这是近年来广泛使用的一种惩罚函数.第2种是硬截断Hard惩罚函数[6],这种惩罚函数来自于小波截断准则,在某种程度上对应于最优子集选择.第3种是SCAD惩罚函数[4],某种程度上SCAD可以看成是LASSO和Hard的综合.第4种是弹性网惩罚函数,记为EN[7].还有一种是自适应的LASSO惩罚,记为ALASSO[8].
2 计算过程
在模型(1)中,β的最终估计是方程(4)的解.本文采用文献[14]提出的MM(majorize-minorize)算法,具体计算过程如下:
a.对一个给定的λ值,计算β的初始值β(0).本文取Ri(α)为单位阵,ψ(x)=x时估方程(2)的解作为初始值.
b.用β(k)表示第k次迭代所得的解,k≥0,则
β(k+1)=β(k)+[Dβ(k)+Δλ(β(k))]-1UP(β)式中,D为d阶导数阵∂(U(β))/∂β.

式中,ε为一个很小的正数,本文计算时取ε=10-6.
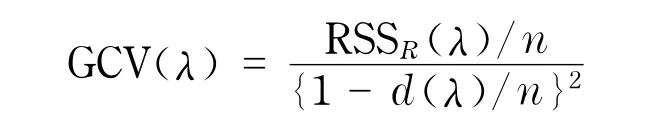
式中,RSSR(λ)是稳健化的残差和W(ψ(Y-/σ))2,Y=(Y1,…,Yn)T,X=(XT1,…,XTn)T,W= diag(W1,…,Wn),d(λ)=tr[(D+Δλ)-1)D].
e.取λ=arg minλGCV(λ)为最终用的λ,然后再进行第a—e步,算出最终的β^.
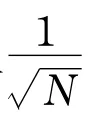
本文主要求β的估计,但计算过程中涉及到多余参数α和σ的估计问题.本文对σ的估计采用和文献[11]类似的方法,取

α的估计依赖于工作相关阵R(α)的形式,对各种常见的工作相关阵,采取和文献[13]相同的估计方法.
3 数值模拟

为了考察本文所提方法的稳健性,通过3种污染数据方式产生数据中的异常值.污染1是随机挑选1个xij把它替换成xij+5.污染2是随机挑选1个xij把它替换成xij+5,并且同时将随机挑选的另外1个yij替换成yij+10.污染3是将污染2中污染的个数变为3个.
衡量变量选择方法优劣的标准有3个.第一个是模型误差ME,采用文献[4]中的定义方式.

在表1中,SCAD-R表示在惩罚函数SCAD下稳健方法,SCAD-NR表示在惩罚函数SCAD下非稳健方法,其余符号的含义类似.从表1可以看出,在使用各种惩罚函数的情况下,当数据集中含有异常值的时候,通常的非稳健方法会受到强烈的影响,尤其是使用EN惩罚函数的时候.由于非稳健方法对方差估计的不稳定,造成其在变量选择方面的波动.相比之下,稳健方法对异常值就有比较强的抵抗力,引入权重函数和有界的得分函数能够大大降低异常值引起的模型误差,尤其是在污染3的情况下.同时,稳健方法在数据存在异常值的情况下,能够在一定程度上挽回完全选对的比例.

表1 不同惩罚函数下稳健方法与非稳健方法表现的比较Tab.1 Comparision between robust and non-robust methods under different penalty functions
4 实例分析
将本文提出的稳健变量选择方法应用到文献[16]的妇女黄体酮纵向数据集中,这批数据共收集了34位妇女在1个月经周期内的尿样,并检测黄体酮水平.将每位妇女的每次尿检看作1次观测,则这批数据共有34个个体,每个个体的观测次数从11~28不等,共收集了N=492次观测数据.将每次观测到黄体酮水平的对数作为因变量,自变量包括测量时间、被测者年龄和被测者身体质量指数.
用Yij表示第i个妇女的第j次观测因变量值,Tij表示观测时间,Ai表示第i位妇女年龄,Bi表示第i位妇女的身体质量指数.该组数据已有多位作者研究过.文献[17]对该组数据拟合了一个半参数混合效应模型,研究的结论是年龄A和身体质量指数B对因变量的影响不显著,而时间T对因变量的影响是显著的,而且时间T对因变量的影响是非线性的.文献[2]用半参数混合模型来检测该批数据的异常值.本文对该批数据拟合线性回归模型为
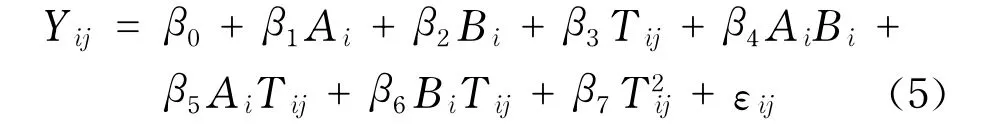
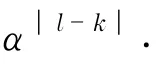
为了检测这批数据中的异常值,计算了每个观测值的权重,用sij表示第i个个体的第j次观测的权重,sij按公式计算.
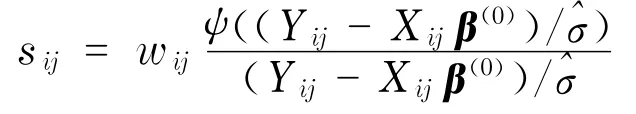
式中,β(0)为式(2)的解;Xij=(1,Ai,Bi,Tij,AiBi,AiTij,BiTij,T2ij).各个观测值的权重如图1所示.

图1 492个观测值的权重Fig.1 Weights of 492 observations
从图1可以看出,第18个个体观测值的权重较低,低于0.4,尤其是第244个和第263个观测值的权重相对较低,低于0.3.这表明第18个个体,尤其是第244个和第263个观测值是异常值.这个结果在某种程度上和文献[2]的结果一致.根据文献[2]的研究结果,第18个个体中的观测值是强影响点.
现将本文的稳健变量选择方法应用到该批数据,所得结果如表2所示(见下页).
表2中的数据表示模型(5)中回归系数的估计值,0表示该系数被估计为0,或者说模型不选择该系数所对应的自变量,认为它对因变量影响不显著.从表2可以看出,5种惩罚函数对应的惩罚估计都认为模型中应该包含截距项、时间T和时间T的平方项,而认为年龄A和身体质量指数B以及交互效应都对因变量没有显著影响,不应包含在模型中.这个分析结果和文献[2,17]的分析结果类似.
为了考量本文方法的稳健性,进一步用交互验证的方法比较稳健和非稳健两种方法的表现.每次剔除1个个体的数据,用剩余的33个个体的数据估计式(5)中的回归系数,并且用平均均方误差MSE来衡量各个方法在交互验证过程的稳定性,定义

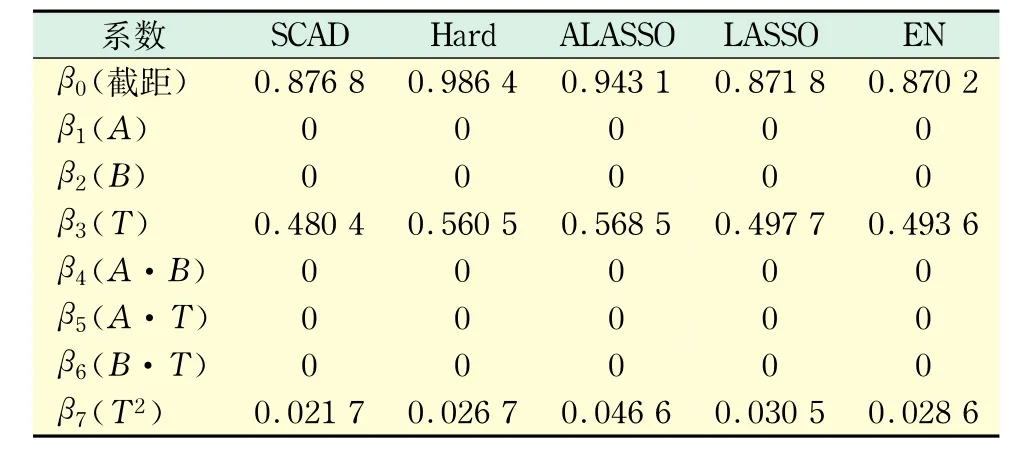
表2 不同惩罚函数下黄体酮数据的分析结果Tab.2 Results for progesterone data under different penalty functions
MSE越小,表示该方法越稳健.计算结果如表3所示.
表3中的数值是MSE的值,这里非稳健方法指的是计算的过程中取ψ(x)=x,wij=1.从表3可以看出,非稳健方法的MSE比稳健方法对应的MSE要大,仅有LASSO方法除外.因此,从大体上来说,稳健方法得到的结果比较稳定,分析结果不易受到异常值的影响.

表3 稳健和非稳健方法的比较Tab.3 Comparison between robust and non-robust methods
5 结束语
将文献中已有的变量选择方法和稳健估计方法结合起来,提出了一类针对纵向数据线性回归模型的稳健变量选择方法,该方法先将通常的估计方程稳健化,然后结合一些常用的惩罚函数,构成稳健的惩罚估计方程,通过解该方程获得模型回归系数的估计.加惩罚函数的作用是能将很小的回归系数估计为零,从而达到在估计的同时进行变量选择,选出真正对因变量有影响的自变量.将估计方程稳健化的作用是当数据中含有异常点时,估计结果能保持相对稳定性.将稳健的变量选择方法应用在模拟实验和实际数据上的应用结果显示,当数据中含有异常点时,稳健方法比非稳健方法更加稳定.
[1] Miller A.Subset selection in regression[M].London:Chapman and Hall,2002.
[2] Fung W K,Zhu Z Y,Wei B C,et al.Influence diagnostics and outlier tests for semiparametric mixed models[J].Journal of Royal Statistical Society,Ser B,2002,64(2):565-579.
[3] 王大荣,张忠占.线性回归模型中变量选择方法综述[J].数理统计与管理,2010,29(4):615-627.
[4] Fan J,Li R.Varible selection via nonconcave penalized likelihood and its oracle properties[J].Journal of the American Statistical Association,2001,96(456):1348 -1360.
[5] Tibshirani R.Regression shrinkage and selection via the lasso[J].Journal of Royal Statistical Society,1996,58(1):267-288.
[6] Donoho D L.Ideal spatial adaptation by wavelet shrinkage[J].Biometrika,1994,81(3):425-455.
[7] Zou H.Regulariztion and variable selection via the elastic net[J].Journal of Royal Statistical Society,Ser B,2005,67(2):301-320.
[8] Zou H.The adaptive lasso and its oracle properties[J].Journal of American Statistical Association,2006,101(475):1418-1429.
[9] Fan J.A selective overview of variable selection in high dimensional feature space[J].Statistica Sinica,2010,20(1):101-148.
[10] Preisser JS.Robust regression for clustered data with application to binary responses[J].Biometrics,1999,55(2):574-579.
[11] He X.Robust estimation in generalized partial linear models for clustered data[J].Journal of American Statistical Association,2005,100(472):1176-1184.
[12] Sinha S K.Robust inference in generalized linear models for longitudinal data[J].Canadian Journal of Statistics,2006,34(2):261-278.
[13] Liang K Y.Longitudinal data analysis using generalized linear models[J].Biometrika,1986,73(1):13-22.
[14] Hunter D.Variable selection using MMalgorithms[J]. Annals of Statistics,2005,33(4):1617-1642.
[15] 樊亚莉,王林平.AR(1)模型下F检验的性质[J].上海理工大学学报,2005,27(4):295-299.
[16] Sowers M F.Urinary ovarian and gonadotrophin hormone levels in premenopausal women with low bone mass[J].J Bone Min Res,1998,13(7):1191-1202.
[17] Zhang D W.Semiparametric stochastic mixed models for longitudinal data[J].Journal of American Statistical Association,1998,93(442):710-719.
(编辑:石 瑛)
Robust Variable Selection Method and Its Application
FANYa-li1, XUQun-fang2
(1.College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China;2.College of Science,Zhejiang Agriculture and Forestry University,Linan 311300,China)
Based on the variable selection methods and robust estimation methods presnted in literatures,a robust variable selection method was proposed for longitudinal data,and the robustness of the proposed method was evaluated by simulation study.The proposed method was then applied in the analysis of a real data set.It is found from the simulation and analysis of the real data that the proposed robust variable selection method can estimate correctly the regression parameters and select properly the important covariant variables,and it is also robust against outliers in the data set.
penalty function;estimation equation;robustness;variable selection
O 212.1
A
1007-6735(2013)03-0256-05
2012-02-29
樊亚莉(1978-),女,讲师.研究方向:概率论与数理统计.E-mail:yalifan@gmail.com
