基于贝塞尔曲线的机织物三维模拟方法

马崇启，胡传胜，张振波

（天津工业大学 纺织学部，天津 300387）

基于贝塞尔曲线的机织物三维模拟方法

马崇启，胡传胜，张振波

（天津工业大学 纺织学部，天津 300387）

通过对织物中纱线几何结构的分析，提出一种基于Bezier曲线的纱线轴心曲线计算方法.该方法将一个循环内的纱线分为2段，然后根据织物组织结构特点确定待求纱线轴心线上的特征点，接着通过这些特征点反求出第一段轴心线的Bezier控制点，再根据Bezier曲线的光滑拼接条件及已知特征点，计算出第二段轴心线的Bezier控制点，从而建立一个循环纱线的轴线曲线方程.在此基础上，采用放样建模方法建立机织物中纱线的三维几何模型，为机织物的三维模拟奠定基础.该方法计算简便，模拟效果直观，便于实时调整.

Bezier曲线；纱线轴心线；三维纱线建模；放样建模

织物模拟一直是纺织CAD研究领域的一个重要和热点内容，而作为交织成织物的纱线的模拟仿真是模拟逼真织物效果的基础[1]，尤其是在三维织物模拟中，建立较好的纱线形态和外观模型是进行织物模拟的第一步.目前有很多织物CAD软件都能够实现织物外观的模拟，但绝大多数都是2D模拟，而且模拟效果并不理想，因此，越来越多的人开始研究3D纱线和织物模拟，以期能够更加真实地模拟出织物中纱线的空间形态和接近真实视觉效果的织物模拟图[1].郑天勇等[1]对机织物中三维纱线的建模方法进行了研究，其重点讨论了使用NURBS曲面来模拟纱线的表面，并使用纹理映射的方法来模拟纱线表面的粗糙度、捻度等外观效果，模拟效果较好，但并未给出织物中纱线空间屈曲形态的建模方法.马凌洲[2]在Peirce纱线模型的基础上提出了一种由分段函数表示的数学模型，该模型考虑了织物的紧密程度、组织结构、纱线直径等，建立了纱线屈曲形态的分段函数表示式，但对于纱线截面则采用圆形来处理，有待改进.祝双武等[3]探讨了采用Bezier曲线和柏林噪声函数来模拟纱线二维扭曲形态和毛羽的方法，该方法仅限于单根纱线形态模拟，并不适用于模拟织物中纱线的屈曲形态.张瑞云等[4]也对基于Bezier曲线的纱线建模方法进行了讨论，但其并未给出具体数学模型，而且并未就曲线的光滑拼接作出说明.本文在以上研究基础上提出了一种简单有效的模拟方法，即将一个组织循环内纱线分为2段进行研究，用三次Bezier曲线进行拟合，通过纱线轴心线上的特征点反求出Bezier控制点，并实现2段曲线的光滑拼接.本文还介绍了纱线放样建模方法，并在VC++6.0和openGL编程环境中进行了三维纱线和织物模拟.

1 基于Bezier曲线确定纱线轴心线曲线方程

1.1 Bezier曲线的定义

Bezier曲线是一种样条线，它的数学定义最早由法国雷诺汽车公司工程师Bezier提出[5].Bezier曲线是一种参数多项式曲线，它是由一组控制点惟一定义的，其参数方程表示如下：

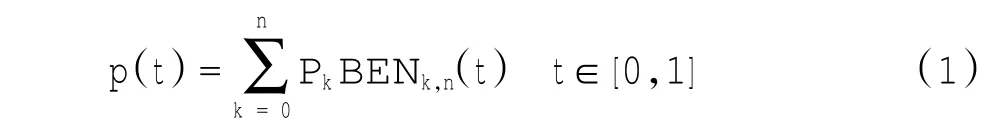
公式（1）是一个n次多项式，具有n+1项，n+1是控制点的个数.因此，控制点越多，该方程的次数越高.

p（t）是通过计算得来的曲线上的点坐标（向量）.将这些点连接起来就可以得到平滑的Bezier曲线.其中pk（xk，yk，zk）表示第k个控制点坐标（向量形式）.

BENk，n（t）是Bernstein基函数，其函数式如下：

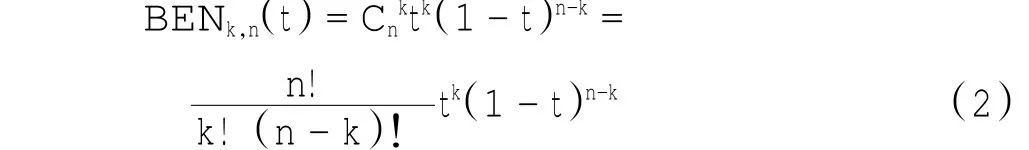
式中：k=0，1，2，…，n，且当k=0，t=0时，tk=1，k!=1.

参数t在[0，1]区间取值，t每取一个值，便可由公式（1）、（2）计算得到一个点p（t），即曲线上的一个节点.当t取0时，p（t）等于一个控制点P0，当t取1时，p（t）等于最后一个控制点Pn.曲线上的点p（t）与t的取值一一对应，因此，t取值个数的多少决定得到的节点p（t）的个数，也就决定着曲线的平滑度.t的取值越多，曲线也就越平滑.Bezier曲线示意图如图1所示.

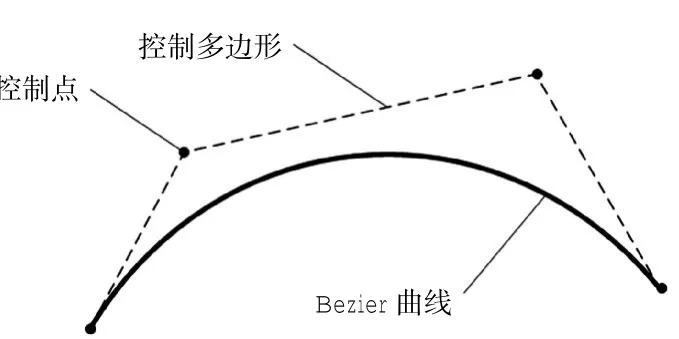
图1 Bezier曲线示意图Fig.1 Bezier curve schematic diagram

由以上定义不难看出，Bezier曲线上每个点均可由控制点坐标加权计算而来，加权值由 t值和Bernstein基函数确定.

1.2 建立纱线轴心线模型

理论上，可以用任意数目的控制点逼近出一条Bezier曲线，但是高次Bezier曲线计算比较复杂，而且还有许多问题有待于理论上解决.因此，实际应用中往往使用三次Bezier曲线拼接的方法来定义曲线[5].

本文亦采用2段三次Beizer曲线拼接的方法来描述织物中一个组织循环内纱线的轴心曲线.需要注意的是，为了使曲线在拼接处光滑，必须满足2个条件[5]：①前一段Bezier曲线的末点必须和后一段Bezier曲线的起点重合（即拼接点）；②拼接点必须与其两侧相邻的控制点满足三点共线.

考虑到以上条件，确立计算过程如下：根据织物中组织点上下交错规律将一个组织循环的纱线分为2段进行研究，根据纱线的几何结构关系，确定纱线轴心线上几个特征点，然后由这些特征点反算出Bezier控制点，从而得到第一段Bezier曲线.然后，根据曲线光滑拼接的条件，计算出第二段Bezier曲线的控制点.这样就能得到2段轴心线的方程，并且实现2段轴心线的光滑拼接.模型示意图如图2所示.

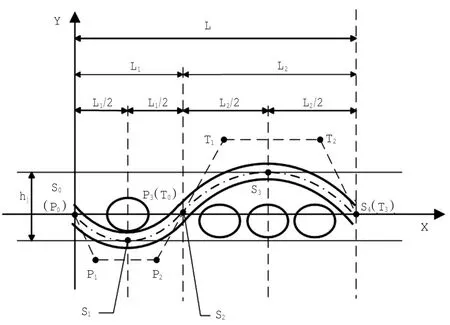
图2 织物经向截面示意图（一个组织循环）Fig.2 Fabric warp yarn direction cross diagram

本文以3/1斜纹组织织物为例进行分析，图2中屈曲的为经纱.X轴和左起第一根纬纱截面横轴重合，X轴与经纱轴心曲线交于点S0、S2、S4，令S0为坐标原点，并以点S2为分界点将经纱分为2段进行分析，同时假设2段纱线屈曲形态为轴对称，其对称轴与经纱轴心曲线的交点分别为S1、S3.

1.2.1 经纱轴心线上特征点的确定

图2中，L表示一个组织循环内的经纱在水平方向的长度；Rw表示一个组织循环纬纱数，本例为4；Pw表示纬密（根/10 cm）.因此L=（100/Pw）×Rw.由于计算中用到的经密Pj、纬密Pw是考虑织造缩率后的实际经纬密度值，所以计算结果更加接近真实情况.

L1、L2分别为点S0S2、S2S4之间的水平距离，并将其值做近似处理，分别令L1=（Rj1/Rj）×L，L2=（Rj2/Rj）×L.其中：Rj表示一个组织循环经纱数；Rj1表示一个组织循环中的纬组织点数；Rj2表示一个组织循环的经组织点数.对于本例，Rj=4，Rj1=1，Rj2=3.

点S1、S3的坐标计算式如下：

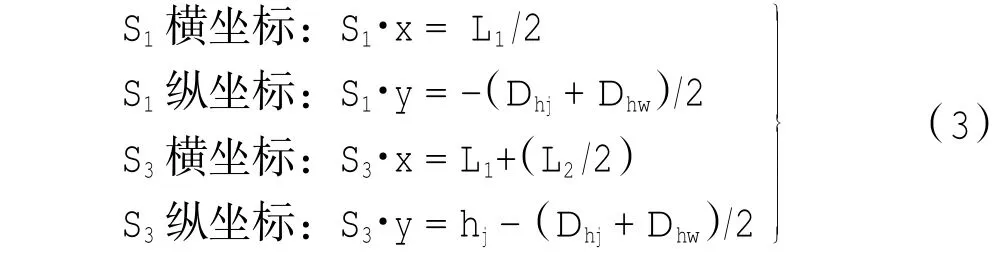
式中：Dhj、Dhw分别表示经纬纱截面高度（计算方法见下文1.2.4）；hj表示经纱屈曲波高.

通过对织物中纱线的几何结构分析，经纱轴心线上的特征点便可确定，接下来便可根据这些点反算出Beizer曲线的控制点.

1.2.2 计算第一段经纱轴心线的控制点

第一段Bezier曲线的控制点为P0、P1、P2、P3，由Bezier曲线的性质可知，P0、P3必然与第一段曲线的起始点S0、终点S2重合.并且由公式（1）可知，当t分别取t0=0，t1=0.5，t2=1时，计算得到得点分别对应为S0、S1、S2.根据文献[6]，采用最小二乘法拟合即可反求出另外2个控制点P1、P2.

计算公式为：

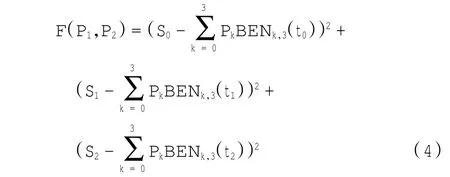
式（4）分别对P1、P2求导，并满足

0，即可求的点P1和P2.

1.2.3 计算第二段经纱的轴心线的控制点

第二段轴心曲线的控制点分别为T0、T1、T2、T3，由Bezier曲线光滑拼接条件①可知，第二段曲线的第一个控制点T0=P3.另外，它的最后一个控制点T3与曲线终点S4重合.因此，求出T1、T2即可，如图3所示.

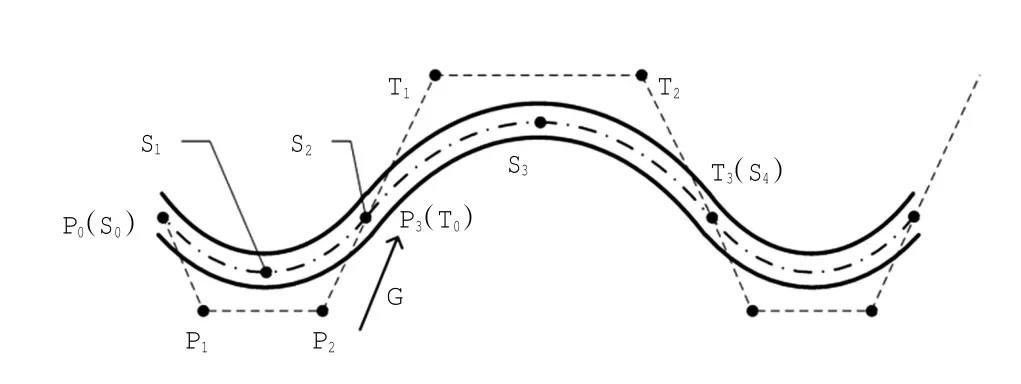
图3 经纱轴心线控制点示意图Fig.3 Bezier control points of warp yarn axis curve diagram

根据Bezier曲线光滑拼接条件②，前后2段曲线的控制点P2、P3（T0）、T1必须共线，为此，令T1=T0+G×R，R值待求.对于第二段Bezier曲线，t0= 0，t1=0.5，t2=1分别对应曲线上的点S2、S3、S4.同上所述方法，得到公式（5）：

式（5）分别对R、T2求导，并令可求得R、T2，由T1=T0+G×R可求出T1.

至此，便分别得到了2段纱线轴心线的控制点，并且由这些控制点定义的2段曲线能够光滑的拼接成一个循环的纱线轴心线.同时由于曲线的对称性，所以多个循环之间的拼接亦是光滑的.

1.2.4 织物中纱线截面形态的确定

因为织物中纱线的交织和挤压，纱线截面处于一种被压扁的状态.根据改进的Peirce织物模型，本文选取椭圆形截面进行模拟，压扁示意图如图4所示.

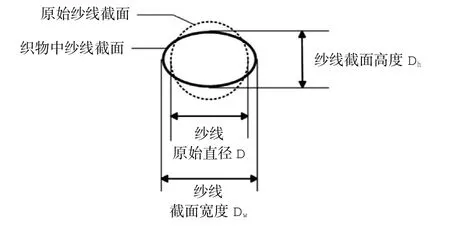
图4 织物中纱线的压扁示意图Fig.4 Yarn flattening schematic diagram

压扁后的纱线截面高度Dh=D×η（纱线压扁系数），Dw=D×δ（纱线延宽系数）.η和δ分别由实验测定或根据经验值给出.

2 建立三维纱线模型

确定了纱线的轴心曲线和纱线截面形态以后，便可建立纱线的三维模型.本文采用放样建模方法.它是一种基于路径和截面的建模方法，即截面沿着路径移动并重复绘制便可形成一个三维图形[6].

根据放样建模思路，在进行纱线计算机模拟时，需要计算轴心线上点的切向量，并将切向量归一化后指定为该点处纱线截面的法向量.基于该法向量，将纱线截面进行旋转，平移、复制到该点处.纱线截面的旋转、平移涉及坐标矩阵的计算，此处不做详细说明.重复以上步骤即可得到一些列沿纱线轴心线排列的截面，最后将各截面依次连接起来便形成了完整的三维纱线外观.建模过程如图5所示.

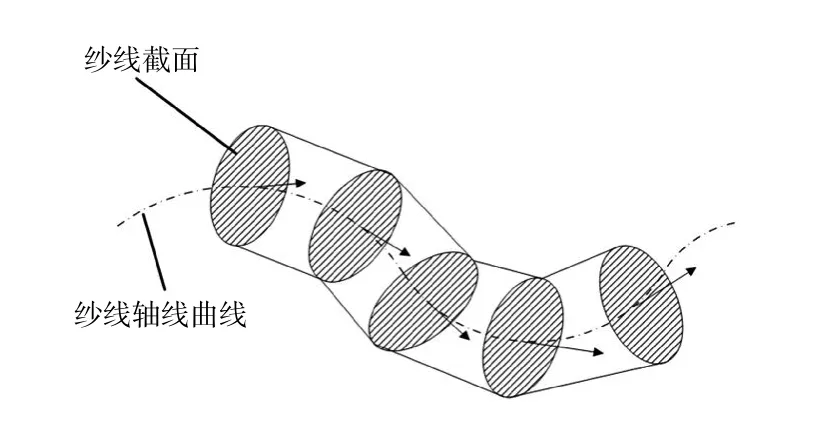
图5 三维纱线放样建模示意图Fig.5 3D yarn modeling diagram

纱线表面平滑度取决于截面的多少，截面越多，纱线外观越平滑，但是计算量也会越大.所以，编写OpenGL绘图程序时应选取适当的值.

3 纱线及织物模拟效果图

根据上述分析，本文对一种规格的牛仔面料进行了模拟，模拟过程及效果图如图6~图8所示.

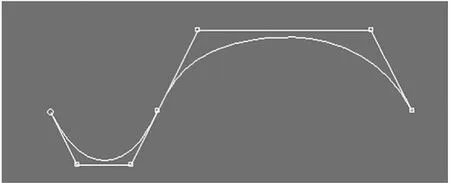
图6 一个循环的经线轴心线及其控制点Fig.6 One repeat of yarn and it′s control points

图7 经纱模型Fig.7 Warp yarn medel

图8 三维织物模拟图Fig.8 3D fabric simulation

牛仔面料规格为：383 g纯棉牛仔面料，经纬纱细度均为84 tex，经纬密度分别为283根/10 cm，173根/ 10 cm，幅宽为147~152 cm，3/1右斜纹，蓝色.

4 结束语

本文对织物中纱线的几何结构进行了分析和计算，给出了纱线轴心线上几个特征点.根据这些特征点并基于Bezier曲线先后计算得出2段纱线的轴心线控制点，然后将2段曲线拼接成一个完整循环的纱线轴心曲线.由于计算时考虑了Bezier曲线光滑拼接的条件，并且假设纱线具有对称性，所以保证了纱线轴心曲线的光滑性.最后经实例模拟可见，模拟效果基本上能够反映纱线在织物中的屈曲形态，取得了预期效果.

该方法在模拟一些单层的、具有简单组织结构的织物时较为可行，但是对于复杂织物还有待完善，比如多层织物，浮长线比较长的织物.另外，本文只探讨了织物中纱线因组织点变化而产生的上下屈曲形态，并未考虑由于同系统纱线之间的相互挤压及与另一系统纱线的作用而导致纱线侧向扭曲，对纱线表面粗糙度、捻度、毛羽的模拟也暂未涉及，在后续研究中将会进一步完善.

[1] 郑天勇，黄故.机织物中纱线3D模型的建立[J].纺织学报，2002，23（2）：93-95.

[2] 马凌洲.计算机辅助织物创新设计与制作系统的研究与实现[D].杭州：浙江大学，2005：62-69.

[3] 祝双武，韩惠民，任亮.基于贝塞尔曲线及柏林噪声模型的纱线外观仿真[J].西安工程大学学报，2009，23（1）：23-25.

[4] 张瑞云，黄新林，李汝勤.机织物的计算机三维模拟[J].纺织学报，2005，26（1）：62-63.

[5] 陈传波，陆凤.计算机图形学基础[M].北京：电子工业出版社，2006：222-228.

[6]亓鑫辉.ds Max火星课堂[M].北京：人民邮电出版社，2011：18.

[7] 韩丽娜，耿国华.使用多段Bezier曲线模型的地质等值线光滑算法[J].计算机工程与科学，2010，32（11）：63-65.

3D weave fabric simulation method based on Bezier curve

MA Chong-qi，HU Chuan-sheng，ZHANG Zhen-bo
（School of Textiles，Tianjin Polytechnic University，Tianjin 300387，China）

A yarn axis curve calculation method based on the Bezier curve is put forward according to yarn geometrical structure in the weave.This method divides one repeat of the yarn into two sections,and then works out the feature points in the yarn axis.Afterwards,figures out the Bezier control points of the first section axis,then according to the Bezier curve smooth splicing conditions and the feature points,calculates the second section axis Bezier control points.At last,one repeat of the yarn axis curve is established.On the basis of the yarn axis curve, using lofting modeling method to simulate 3D yarn in the weave fabric,which sets the foundation for 3D weave fabric simulation.This method is simple and the simulation effect is visualized,so it′s convenient for real-time adjustment.

Bezier curve；yarn axis；3D yarn modeling；lofting modeling

TS106.4

：A

：1671-024X（2013）01-0018-04

2012-09-28

马崇启（1964—），男，教授，硕士生导师.E-mail：tjmcq@tjpu.edu.cn