等离子体激励位置对抑制压气机角区分离效果的影响

2013-07-07梁斐杰陆利蓬柳阳威孙槿静

航空发动机 2013年4期

关键词：叶栅总压吸力

梁斐杰，陆利蓬，柳阳威，孙槿静

（北京航空航天大学能源与动力工程学院，北京100191）

等离子体激励位置对抑制压气机角区分离效果的影响

梁斐杰，陆利蓬，柳阳威，孙槿静

（北京航空航天大学能源与动力工程学院，北京100191）

为了揭示等离子体气动激励对角区分离的作用效果，应用FLU EN T软件数值模拟了等离子体激励器对压气机叶栅角区分离的影响。采用等离子体激励器的简化唯象模型，在压气机叶片吸力面和端壁不同位置沿流向施加激励，对总压损失系数、极限流线、不同截面流动情况进行了比较分析。结果表明：吸力面激励对角区分离改善有限，角区未失速时，近分离点前是激励最佳位置，角区失速后，激励位置越靠前效果越好；端壁流向激励能明显减小角区分离损失，分离点至叶片前缘任何位置施加激励效果一样；组合激励同时减小吸力面边界层和端壁边界层损失，使角区分离消失且不受攻角变化影响。

角区分离；流动控制；等离子体激励；唯象模型；数值模拟

0 引言

未来压气机发展的主要趋势是更高的增压比，更高的效率和更宽的稳定工作范围，但流动分离却导致了压气机性能的降低[1]。其中，在吸力面和端壁之间形成的角区分离流动，是压气机内部普遍存在的1种流动分离现象，是压气机内流动损失和流动堵塞的主要来源[2]，严重时引起失速和喘振[3]。因此，对压气机3维角区分离流动机理、预测和控制的研究，始终是高性能先进压气机设计中关注的重点问题，也是内流湍流研究的关键科学问题[4-5]。

压气机角区分离是典型的3维分离，不同于2维分离，角区分离是在端壁及吸力面表面均有回流的区域，结构复杂[6]。端壁出现明显的大回流区时，又称之为角区失速，会对性能造成更大的影响[7]，更需要进行有效控制。近年来，流动控制技术得到了快速发展，包括主动控制技术和被动控制技术2类。其中，等离子体流动控制技术是1种基于等离子体气动激励的主动控制方法，具有响应迅速、作用频带宽、无需移动机械部件、便于实时控制、功率消耗低等优点。等离子体流动控制技术在抑制翼型前缘流动分离[8]、抑制涡轮[9-10]和压气机[11-13]流动分离等方面已经取得了一定的进展。但相关控制机理和规律还有待进一步研究，目前还没有工程应用中的压气机采用了等离子体激励控制流动分离。

本文采用FLUENT软件数值模拟研究了不同攻角下等离子体激励位置对抑制压气机叶栅角区分离效果的影响。数值计算中，等离子体激励的模型采用Shyy等提出的唯象模型，通过FLUENT软件自带的UDF二次开发模块实现添加。研究算例采用剑桥大学的高负荷PVD叶栅，通过在叶片吸力面和端壁不同位置施加激励，系统研究了等离子体气动激励位置抑制压气机叶栅角区分离流动的作用效果。

1 等离子体气动激励原理及模型

1.1 等离子体气动激励原理

等离子激励器结构[14]如图1所示，将2层电极用绝缘介质薄膜隔开，其中1层电极完全暴露在空气中，另外1层电极则被绝缘介质所覆盖。在2电极之间施加较高电压时，电极间的气体会发生电离，形成了大气压下均匀辉光放电等离子体，产生的等离子体对电极附近的带电粒子作用体积力，从而使这些带电粒子和中性的空气粒子相互碰撞，并将动量传递给空气粒子，使其发生运动，最终对流动产生加速作用。

图1 等离子激励器结构

1.2 等离子体气动激励数学模型

采用由Shyy等提出的唯象模型，该唯象模型[15]基于试验和理论分析，假设等离子体的作用区域如图2所示，其中宽度为b，高度为a的直角三角形AOB，

图2 等离子激励器作用区域

式中A，B，C3项与通常的控制方程一样，D项通过式（5）求解，即在该区域内电场力呈线性分布，在三角形AOB以外的区域，电场强度的大小不足以击穿空气，所以三角形AOB区域为等离子体激励器的有效击穿区域。在原点O具有最大电场强度，在边界OA、OB及AB上截断电场强度为Eb。

整个三角形区域里面电场力平行于AB边界并呈线性变化，因此可以给出电场分布为

式中：U0为激励电压；d为电极间的间距；根据电场线性分布可知

通过式（1）中的电场强度分布可得该区域内的电场力分布为

式中：ϑ为施加电压的频率；α为电荷碰撞效率因子；ρc为电荷密度；ec为电子电荷常数；△t为激励电压的半周期；δ为狄拉克函数；Eb为电场边界截止电压。

为了模拟等离子体激励器诱导的体积力对于流动的作用效果，在N-S方程中添加相应的体积力项。假设流动是定常不可压的低雷诺数流动。控制方程为

2 数值方法

2.1 算例简介

研究所选用的压气机叶栅是英国剑桥大学Gbadebo等人针对角区分离流动机理研究所设计的高负荷平面叶栅，运用试验和数值模拟方法系统研究了其内部的3维角区分离流动。该叶栅是1种典型的PVD（Prescribed Velocity Distribtion）叶栅，叶型主要参数见表1。

表1 叶栅信息

2.2 计算网格

计算网格由NUMECA软件的AutoGrid模块生成，采用分区结构化网格，为O-4H型网格，网格块间所有连接网格都是完全匹配的，以避免计算中引入插值误差，所有壁面第1条网格线y+<1.4。由于该流动具有对称性，为减小计算量，只计算半个叶高，在叶中采用对称边界条件即可。为了减小网格对计算的影响，计算过程中数值试验了一系列网格，通过调整网格数和网格分布情况，得到网格无关解。最终使用的网格如图3所示，展向网格数为51，网格总数944800。

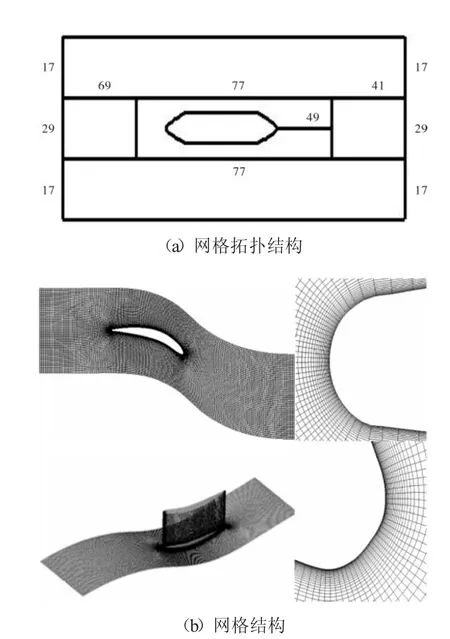
图3 计算网格

2.3 计算设置

计算采用FLUENT软件，湍流模型选用RSM模型，压力速度耦合求解采用SIMPLE算法，对流项和扩散项分别采用2阶迎风格式和中心差分格式进行离散。进口给定速度分布，出口给定静压，叶中采用对称边界条件，固壁采用绝热无滑移边界条件。

2.4 等离子激励器说明

研究中等离子激励器的作用区域为a=1.5 mm，b=3 mm。施加电压的频率ϑ=3 kHz；电荷密度ρc=1× 1011cm-3；电子电荷常数ec=1.602×10-19；放电时间△t=67 μs；电场边界截止电压Eb=30 kV/cm。

对等离子体激励的数值模拟，通过FLUENT软件的UDF（User Defined Functions）功能进行二次开发实现。等离子激励器在不同位置施加方案如图4所示，分别在叶片吸力面沿弦长0%，30%，60%，90%及端壁对应位置模拟等离子体气动激励，从左到右分别为位置1～4。

图4 等离子激励器作用位置

3 结果及讨论

3.1 不加等离子体气动激励的流动分析

为保证计算结果的可靠性，首先，对不加等离子体气动激励0°攻角下的PVD叶栅进行了校验，其中试验结果由英国剑桥大学Gbadebo等人完成[4]。端壁和吸力面的极限流线对比情况如图5所示，从定性上看计算得到的角区分离和试验吻合得很好。

在不加等离子体气动激励的情况下，对攻角为1°，3°，5°，7°的工况进行了计算，并进行极限流线对比如图6所示。随着攻角的增大，吸力面分离逐渐增大，3°攻角时，端壁出现很大的分离流动，形成角区失速，使其性能急剧恶化。

3.2 吸力面不同位置施加激励的流动分析

图5 0°攻角计算与试验极限流线对比

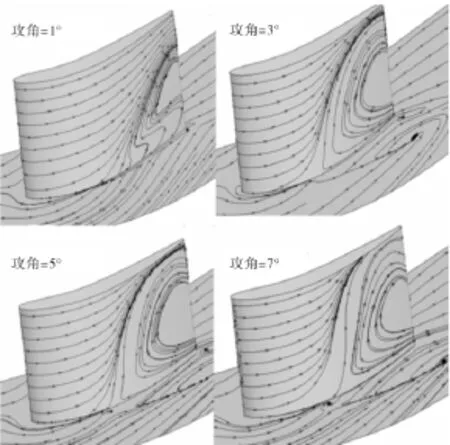
图6 不同攻角下的极限流线对比

对应每1个攻角的原始流动，在吸力面的4个位置施加等离子体气动激励，选择攻角为1°和5°的工况进行分析分别如图7、8所示。对比发现，在吸力面施加激励可以显著改善吸力面上的分离流动，使回流区面积减小，但对端壁的分离流动改善有限。

首先，攻角为1°时，未发生角区失速，在位置3施加激励可使吸力面分离几乎消失；其次是在位置1和位置2施加激励，二者效果相当；再次，在位置4施加激励效果不明显。此时位置3更靠近分离点。当攻角为5°时，角区发生失速，此时激励位置越靠前效果越好。

激励位置相同，攻角不同时，在位置1和位置2施加激励都能使吸力面的流动分离得到有效控制，端壁变化则不明显。随着激励位置后移，激励效果逐渐减弱，极限流线几乎不变。

图7 1°攻角时吸力面不同位置施加激励极限流线对比

图8 5°攻角时吸力面不同位置施加激励极限流线对比

对比5°攻角，吸力面不同位置施加激励时，叶片尾缘后50%弦长位置截面的总压损失，如图9所示。

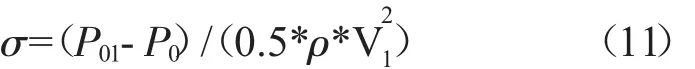
P01，P0，ρ，V1分别为进口总压，当地总压，工质密度和进口速度。可见在吸力面不同位置施加激励都不能使角区分离消失。激励位置越靠前，吸力面边界层的损失越小，角区中心的总压损失系数越小。在前缘施加激励能更好的抑制吸力面边界层损失对角区分离的贡献。

对比了不同攻角，不同位置施加激励的总压损失系数如图10所示。计算同式（11）。攻角为0°和1°时未发生角区失速，此时位置1、2、3都在分离点附近或上游，施加激励总压损失系数变化基本一致。攻角增大到3°，发生角区失速，总压损失急剧上升，激励位置越靠近前缘，总压损失系数越小，位置1施加激励对不同攻角工况都能有效控制。

图9 5°攻角时吸力面不同位置施加激励时叶片尾缘50%弦长截面的总压损失

3.3 端壁不同位置施加激励的流动分析

对应每1个攻角的原始流动，在端壁的4个位置施加等离子体气动激励，并选择攻角为1°和5°的工况进行分析分别如图11、12所示。通过对比发现，端壁施加激励可以显著改善端壁上的分离流动，甚至使分离消失。端壁流动不再是由压力面流向吸力面，而是在施加激励的位置之后，流动与主流相似。

图10 总压损失系数对比

图111 °攻角时端壁不同位置施加激励极限流线对比

图12 5°攻角时端壁不同位置施加激励极限流线对比

激励位置越靠前，端壁流动改善越好，位置1和2效果相似，同时会在吸力面形成回流区并随攻角增大而增大。在靠后的位置施加激励，随着攻角增大，等离子体气动激励对端壁和吸力面的流动改善效果都变得有限，甚至并不会影响吸力面的流动情况。

对比5°攻角，端壁不同位置施加激励时，叶片尾缘后50%弦长位置截面的总压损失如图13所示。发现在端壁位置1和2施加激励，角区失速消失，端壁边界层和吸力面边界层没有出现掺混，而是较好的保持了各自的独立性，形成了损失相对较小的“2维”分离。在位置3、4施加激励，角区失速并不会消失，尤其是在位置4施加激励，变化有限。可见激励位置越靠前，激励效果越好。

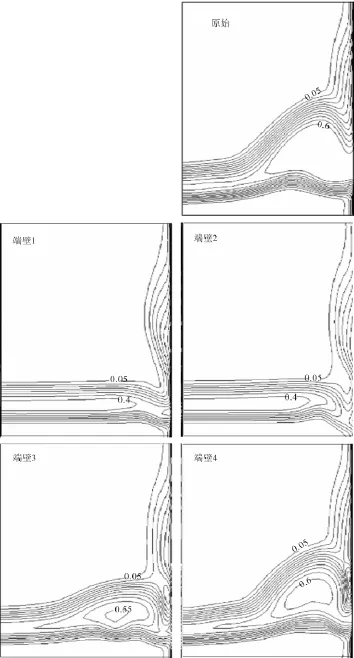
图13 5°攻角时端壁不同位置施加激励时叶片尾缘50%弦长截面的总压损失

在不同攻角下，不同位置施加激励的总压损失系数对比如图14所示。发现在端壁施加激励时，位置1和位置2效果几乎一样，但是随着攻角的增大，位置1有优于位置2的趋势，这是因为分离点会随攻角增大而前移。激励位置越靠后，激励效果越弱。同时，随着攻角的增大，位置1和位置2的激励效果急剧减弱，激励效果对位置的敏感性变差。参考图14说明在大攻角工况下，吸力面边界层2维分离带来的损失加大。

图14 总压损失系数对比

3.4 吸力面和端壁的组合激励

基于以上分析，在端壁位置1和吸力面位置1同时施加激励。并对7°攻角，叶片尾缘后50%弦长位置的周向平均总压损失系数进行了对比如图15所示。采用组合激励的方式，不论在近壁区还是主流区都可以产生很好的流动控制效果，其结合了吸力面激励和端壁激励的优点，使得在整个叶高范围内都有很好的作用效果。

图15 7°攻角工况下周向平均总压损失系数

4 结论

本文采用FLUENT软件数值模拟研究了等离子体激励位置对抑制高负荷压气机PVD叶栅角区分离效果的影响，得到主要结论如下：

（1）吸力面激励可以改善吸力面边界层并减小其对角区分离的贡献，但对角区分离抑制效果有限；端壁激励可以改善端壁边界层流动，可以较好抑制角区分离。

（2）未发生角区失速，近分离点施加激励效果最优；发生角区失速后，吸力面越靠前施加激励抑制效果最好，端壁分离点至叶片前缘任何位置施加激励抑制效果都基本一样。

（3）端壁施加激励对角区分离的抑制效果大于吸力面施加激励，端壁边界层对角区分离贡献更大，是研究控制角区分离的重点。

（4）采取组合激励的方式，可以很好抑制角区分离/失速，且不受攻角变化影响，可以据此发展更经济的组合方式进行控制。

[1]Li Yinghong,Wu Yun,Zhou Min,et al.Control of the corner separation in a compressor cascade by steady and unsteady plasma aerodynamic actuation[J].Expro Fluids,2010,48: 1015-1023.

[2]Denton J D.Loss mechanisms in turbomachines[J].Journal of Turbomachinery,1993,115：621-656.

[3]Thiam A H,Whittlesey R W.Corner separation and the onset of stall in an axial compressor[R].AIAA-2008-4299.

[4]Gbadebo S A.Three-dimensional separations in compressors [D].United Kingdom:University of Cambridge,2003.

[5]Liu Yangwei,Lu Lipeng,Fang Le,et al.Modification of spalart-allmaras modelwith consideration ofturbulence energy backscatter using velocity helicity[J].Physics Letters A, 2011,375（24）：2377-2381.

[6]Joslyn H D,Dring R P.Axial compressor stator aerodynamics [J].Journal of Engineering for Gas Turbines and Power,1985, 107：485-493.

[7]Lei V M,Spakovszky Z S,Greitzer E M.A criterion for axial compressorhub-cornerstall[J].ASMEJournalofTurbomachinery, 2008,130（1）：1-10.

[8]Post ML,Corke T C.Separation control in high angle of attack airfoil using plasma actuators[J].AIAA Journal,2004,42（11）: 2177-2184.

[9]Huang J H,Corke T C.Plasma actuators for separation control of low pressure turbine blades[J].AIAA Journal,2006,44（1）：51-57.

[10]Huang J H,Corke T C.Unsteady plasma actuators for separation control of low-pressure turbine blades[J].AIAA Journal,2006,44（7）：1477-1487.

[11]吴云,李应红.等离子体气动激励抑制压气机叶栅角区流动分离的仿真与实验 [J].航空动力学报,2009,24（4）：830-835. WU Yun,LI Yinghong.Computational and experimental of suppressingplasma aerodynamic actuation cornerflow separation control in a compressor cascade[J].Journal of Aerospace Power,2009,24（4）：830-835.(in Chinese)

[12]刘华坪，陈焕龙，袁继来，等.变冲角条件下等离子体对扩压叶栅性能的影响 [J].航空动力学报,2011,26（8）：1871-1878. LIU Huaping,CHEN Huanlong,YUE Jilai,et al.Influence on the performance of compressor cascade with alterative incidence angles by the plasma[J].Journal of Aerospace Power,2011,26（8）：1871-1878.(in Chinese)

[13]赵小虎,吴云,李应红,等.高负荷压气机叶栅分离结构及其等离子体流动控制 [J].航空学报,2012,33（2）: 208-219. ZHAO Xiaohu,WU Yun,LI Yinghong,et al.Separation structure and plasma flow controlon highly loaded compressure cascade[J].Journal of Aerospace,2012,33（2）: 208-219.(in Chinese)

[14]李纲.等离子体流动控制机理极其应用研究[D].北京：中国科学院工程热物理研究所，2008. LI Gang.Investigation of plasma flow control mechanism and its application[D].Beijing:Chinese Academy of Sciences, 2008.(in Chinese)

[15]Shyy W,Jayaraman B.Modeling of glow dischargeinduced fluid dynamics[J].Journal of Applied Physics,2002,92（11）：6434-6443.

Impact of Plasma Actuating Position on Control of Corner Separation of a Compressor Cascade

LIANG Fei-jie，LU Li-peng，LIU Yang-wei，SUN Jin-jing
（School of Jet Propulsion,Beihang University,Beijing 100191,China）

To explore the intrinsic mechanism of plasma aerodynamic actuation on corner separation,FLUENT was used to simulate the effect of a plasma actuator on the corner separation of a compressor cascade.The phenomenological model was applied to impose actuation on different positions along with the flow direction both at the suction surface and hub.Total pressure loss coefficient,streamline,flow in different cross sections were comparatively analyzed.The results indicate that suction surface actuation reduces corner separation loss limited,the separation point is at the best actuating point without corner stall while the nearer actuation position is,the more effective is with corner stall.Hub actuation reduces corner separation loss obviously,positions from separation point to blade leading edge does not affect the final results. Combination actuation reduces loss of both suction surface and hub boundary layers to result in corner separation disappear and independence with attack angle.

corner separation;flow control;plasma actuation;phenomenological model;numerical simulation