集装箱港口动态泊位指派仿真优化

乐美龙，陈雷雷，2，黄有方

(1.上海海事大学 科学研究院，上海 201306;2.上海海洋大学 工程学院，上海 201306)

0 引言

集装箱是重要的物流单元，集装箱运输已成为最重要的运输方式，在跨国、跨洲的长途运输领域更是如此.集装箱港口是当今最为重要的物流枢纽;泊位是集装箱港口最为重要的资源.泊位指派合理与否，直接影响到集装箱船舶在港口的停泊时间和港口的运营成本，是航运与港口企业能否高效率和高效益运作的关键之一.当今，大型集装箱船的运输和装卸规模越来越大［1］，泊位指派的复杂性也随之增加.

泊位指派可分为离散泊位指派和连续泊位指派.IMAI 等［2］研究多用户港口系统的泊位指派问题，引入离散泊位动态指派的基本模型;此后又在其动态泊位指派模型的基础上引入服务优先级和港口能力限制等因素，对其研究进一步丰富和补充［3-4］.LEE 等［5］探讨连续泊位下的泊位计划问题，给出临域搜索启发式算法，算法中考虑先到先服务以及船舶作业安全间距等实际规则.GOLIAS 等［6］研究顾客服务级别优先程度不同情况下的动态和离散泊位分派问题，建立多目标复合优化模型，并用遗传算法求解.国内也有不少学者对集装箱港口的泊位指派问题进行研究.王军等［7］应用遗传算法研究动态泊位的指派问题，一些学者［8-11］应用仿真方法对泊位服务系统进行仿真建模和分析.当前的研究对泊位指派中以船舶在港时间最短为目标时存在的非线性问题讨论较少，而仿真研究中也缺乏对泊位分配方案的自动生成和优化.近年来，仿真优化作为新的研究领域逐渐被学者们所重视，其基本思想是用仿真模型模拟实际系统，且以仿真结果评估实际系统的性能和参数的优劣，并在上层设计优化算法对仿真结果进行优化，进而达到优化实际系统的目的.就泊位指派问题而言，以仿真技术结合现代智能优化算法探讨泊位指派方案的生成和优化，有较高的研究价值和意义.

1 动态泊位指派问题的数学描述

为了便于描述泊位指派问题的数学模型，作如下假设:

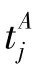
(2)B为泊位的集合，i为该集合中第i个元素，即泊位i，i=1，2，…，I;

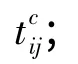
(4)优化目标为船舶在港时间最小，船舶在港时间包含船舶的装卸作业时间和等待时间;

(5)不考虑由于天气等意外因素引起的船舶延迟离港，船舶到港时间已知.

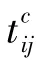
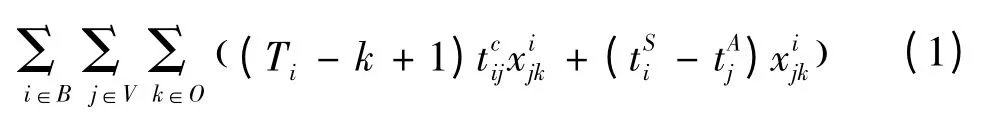
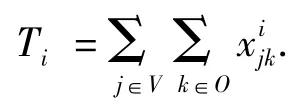
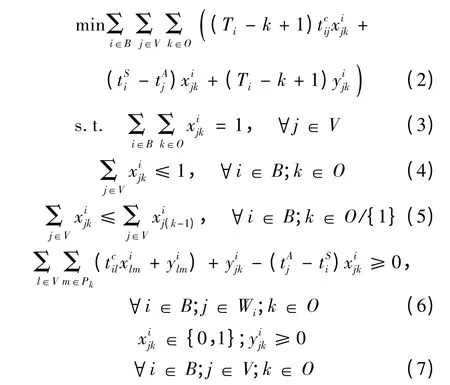
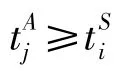
式(3)确保每艘船均接受一次装卸服务，而式(4)确定泊位一次最多服务一艘船.此外，由于船舶在特定泊位接受服务的顺序k是连续排序的，当第k-1 序号无船舶接受服务时，第k 序号应当也无船舶接受服务，式(5)正是该逻辑的约束.式(6)则保证集装箱船只有在到达泊位后才能开始进行装卸服务.

2 动态离散泊位系统仿真建模

2.1 仿真分析

通过以上分析可知，如果应用数学规划模型对泊位指派问题进行求解，其目标函数存在非线性，且随着船舶数量的增长和泊位数量的增加，问题的规模会急剧扩大，因此用求解混合整数规划模型的分支定界法、割平面法等常规求解方法难以求解.仿真技术建立在相似性原理之上，通过对现有真实系统的描述和模拟能够使得真实系统在计算机里再现.越来越多的建模与仿真技术被成功应用于集装箱码头的规划设计和营运管理上［12］.应用仿真方法能够有效解决目标函数非线性问题，在此基础上的泊位指派优化更为高效和精确.

仿真系统可以分为时间推动和事件推动两种类型.在时间推动的仿真系统框架下，系统能够记录仿真实现每一个事件发生的时间点.就离散泊位指派问题而言，不管是静态的还是动态的，其目标函数均为所有船只的在港时间.在仿真的框架下其目标函数即可以表示为

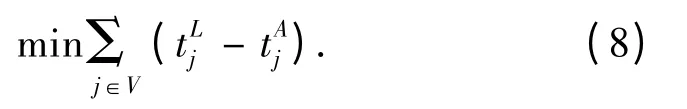
此外，在仿真模型中，约束条件大多由仿真系统的结构保证.在离散泊位指派问题中，式(3)和(4)可通过设置相应仿真元素的容量实现，而式(8)则无须特别考虑，因为在仿真系统中只有主动实体到达才会有相应的仿真事件发生.

2.2 仿真建模

作为集装箱港口的一个子系统，离散泊位系统的主要组成部分有集装箱船舶、泊位、锚地等待区等.根据集装箱船舶靠港的一般过程，泊位指派过程中主要发生的事务依次有:(1)船舶到达;(2)泊位分配;(3)排队等待;(4)装卸服务;(5)船舶离港.具体流程见图1.

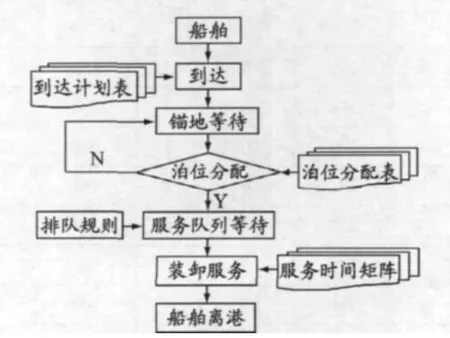
图1 离散泊位系统仿真流程

根据离散泊位系统的基本理论可知，不论是在静态还是动态情景下船舶到达港口的时间都是已知的，所以每艘船舶的到达时间构成船舶到达计划表.在仿真过程中，船舶以此为依据到达港口.泊位分配，则是将所有到达船舶分为若干个子集，每一个子集对应一个具体泊位.每艘船舶和其对应的泊位分配编号构成泊位分配表.仿真过程中，船舶根据泊位分配表进入相应的等待队列，队列内的排队规则为先到先服务.船舶靠泊后，泊位桥吊对船舶进行装卸作业.不同泊位服务不同船只的时间各不相同，于是，相应船舶和对应泊位的装卸服务时间构成船舶泊位服务时间矩阵，以表格的形式体现在仿真系统中.仿真过程中，船舶靠泊后具体服务时间由船舶编号和泊位编号两个量决定.在服务时间矩阵中确定每一次装卸作业的具体服务时间.

3 基于遗传算法的离散泊位指派仿真优化

遗传算法(Genetic Algorithm，GA)［13］是一种借鉴生物界的进化规律(适者生存，优胜劣汰遗传机制)演化而来的随机搜索方法，由美国的HOLLAND教授1975 年首先提出.其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定;具有内在的并行性和更好的全局寻优能力;采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定的规则.由于GA的这些性质，它已被广泛应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域.

GA 对染色体的选择和淘汰的主要标准为适应度函数.而在仿真框架下离散泊位系统的在港时间为每次仿真实验后得到的在港时间值.基于GA 的仿真优化流程见图2.

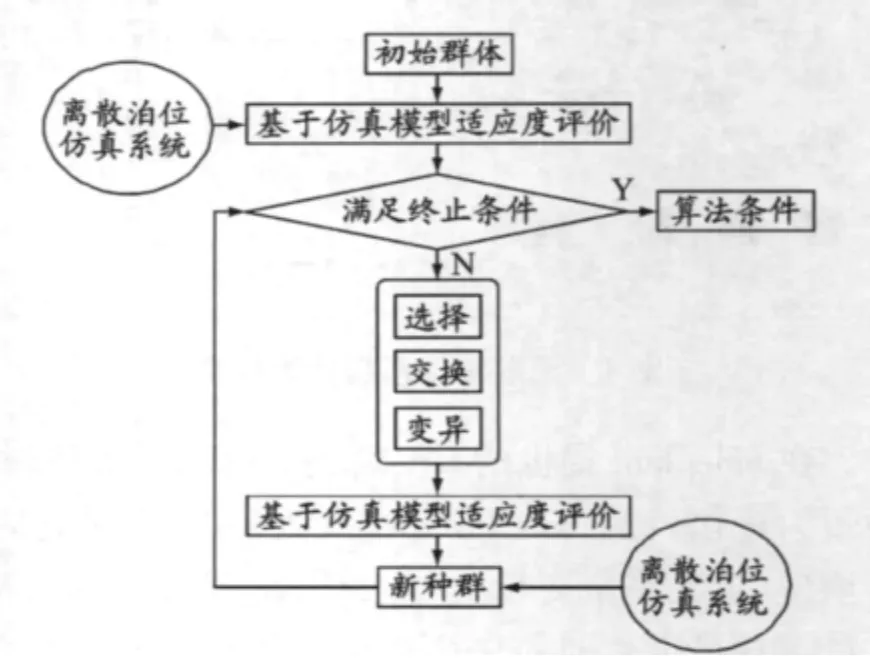
图2 基于GA 的离散泊位系统仿真优化流程

与传统的二进制编码方式不同，仿真优化中可采用每位编码的序号对应相应的船舶，编码的内容为分配的泊位编号，编码的取值范围为集合B，即{1，2，…，I}.以8 艘船、3个泊位为例，其染色体表达见图3，一个染色体个体对应一种泊位分配方案:

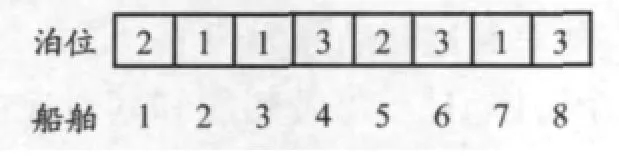
图3 染色体表达实例

4 离散泊位系统仿真优化案例分析

某港口拥有4个泊位，某日有8 艘船舶要求靠泊码头进行装卸服务.8 艘船舶的到达时间和各船舶对应泊位的服务时间见表1.要求确定当日的最佳泊位分配方案，以使得船舶在港总时间最短.

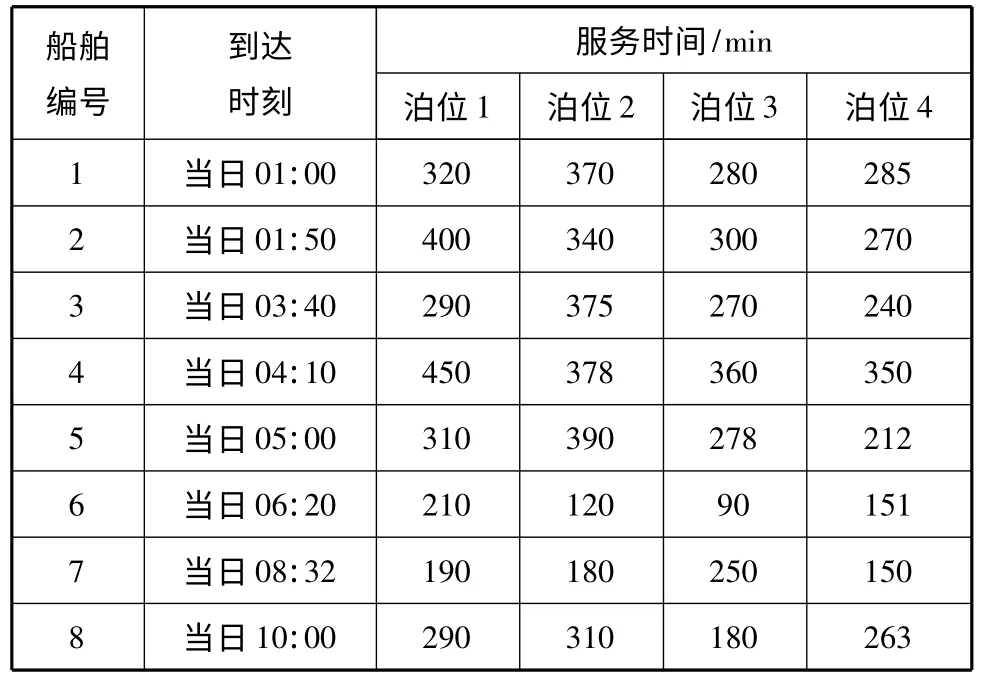
表1 船舶泊位服务时间矩阵

根据该港口实际情况，仿真总体框架见图4.在集装箱船舶进入系统时记录到达时间tAj，在船舶完成作业离开系统时记录离开时间tLj，仿真结束时计算总体等待时间.

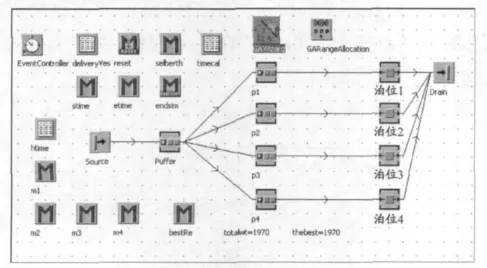
图4 离散泊位系统仿真模型

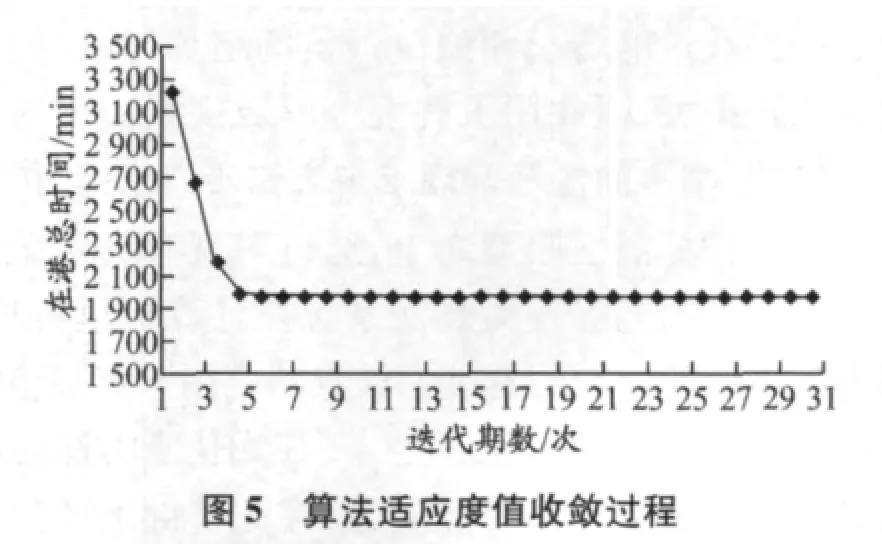
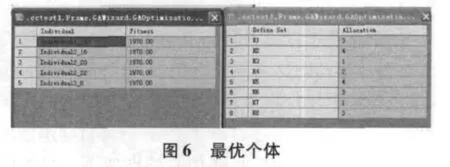
在eM-plant 提供的GA 模块中以总体等待时间最短为优化目标，以{1，2，3，4}为解集分别对应4个泊位，定义决策变量集{K1，K2，K3，K4，K5，K6，K7，K8}，其中的元素对应于染色体上相应编码位的值，并将优化迭代得到的结果作为仿真模型的泊位指派指令.选择交叉概率为0.8，变异概率为0.1.设置种群大小为30，迭代次数为30.模型经过30 代遗传求解，算法的适应度值收敛过程见图5.船舶在港时间最短为2 080 min，最佳分配方案为{3，4，1，2，4，3，1，3}，即1 号船进入3 号泊位，2 号船进入4 号泊位，以此类推，见图6.

港口泊位计划人员在泊位指派过程中一般按照先到先服务的原则，根据贪婪算法安排泊位(人工贪婪算法)，如船舶1 到达时泊位全部空闲则安排至装卸时间最短的泊位3，而船舶2 到达时则安排在泊位4，若泊位全部被占用则船舶等待，若有泊位空闲则安排先到船舶靠泊进行装卸服务.根据该日8 艘船的到达信息及在各泊位的装卸时间，其泊位安排见表2中人工贪婪算法部分.由表2 计算可知，在本案例中用本文提出的基于GA 的仿真优化指派的船舶总体在港时间比人工贪婪算法指派的减少170 min，而且随着到港船舶数量的增加其优势会进一步显现.

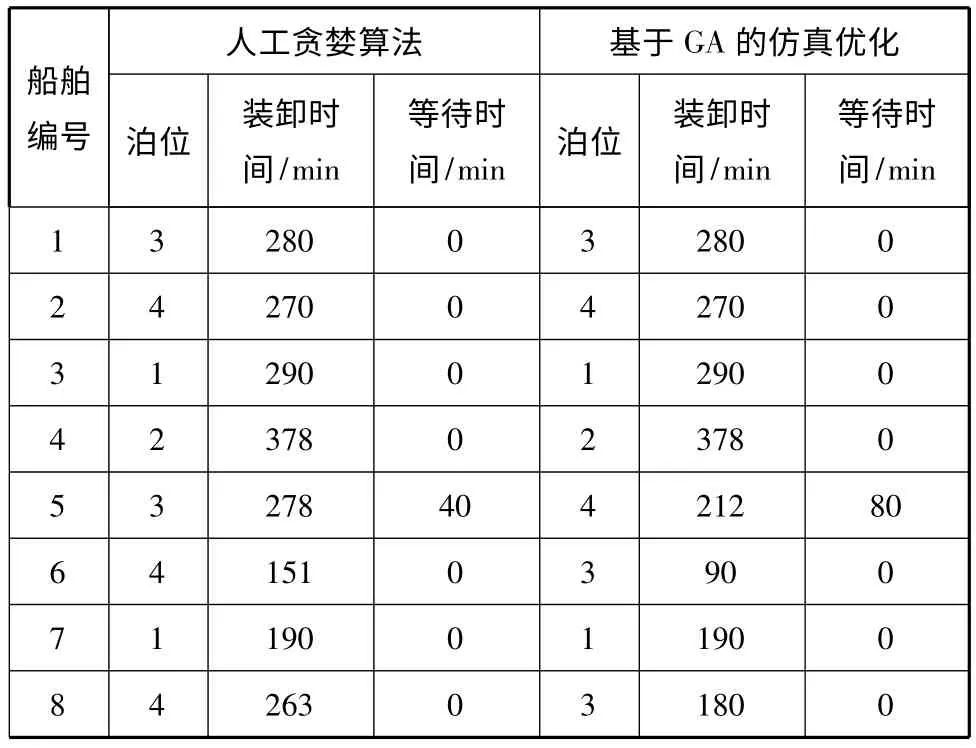
表2 本文方法与人工贪婪算法对比

5 结束语

随着经济的发展和集装箱运输在物流领域的广泛应用，各大港口集装箱的吞吐量也随之增长.面对日益增长的集装箱运输需求，港口间竞争的日益激烈，合理配置资源以提高港口运作效率和效益是必由之路.本文通过建立动态离散泊位指派的数学模型，并在此基础上，提出离散泊位指派的仿真模型和基于GA 的仿真优化方法.运用仿真优化方法，不仅可以很好地解决数学分析中存在的目标函数非线性问题，而且可以通过仿真模型的结构控制取代数学模型中的约束条件.本方法不仅可以提高分析的准确性，而且可以在很大程度上简化求解过程，可用于集装箱港口泊位资源的配置和调度.

当然，集装箱码头的作业系统非常复杂，泊位指派和分配问题除了离散泊位指派问题外还有连续泊位指派的问题.此外，实际操作中，泊位指派计划制订时还需要考虑岸桥计划、堆场计划等.进一步研究可从以下3个方面展开:(1)研究在泊位分配的同时考虑船舶进入泊位的顺序;(2)探索连续泊位指派的仿真优化方法;(3)结合岸桥调度研究泊位指派的仿真优化问题.

［1］VACCA I，BIERLAIRE M，SALANI M.Optimization at container terminals:status，trends，and perspectives［C］// Proc the Swiss Transport Res Conf.Monte Verita/Ascona，2007:1-21.

［2］IMAI A，NISHIMURA E，PAPADIMITRIOU S.The dynamic berth allocation problem for a container port［J］.Transportation Res:Part B，2001，35(4):401-417.

［3］IMAI A，NISHIMURA E，PAPADIMITRIOU S.Berth allocation with service priority［J］.Transportation Res:Part B，2003，37(5):437-457.

［4］IMAI A，NISHIMURA E，PAPADIMITRIOU S.Berthing ships at multi-user container terminal with a limited quay capacity［J］.Transportation Res:Part E，2008，44(1):136-151.

［5］LEE Yusin，CHEN Chuen-Yih.An optimization heuristic for the berth scheduling problem［J］.Eur J Operational Res，2009，196(2):500-508.

［6］GOLIAS M M，BOILE M，THEOFANIS S.Berth scheduling by customer service differentiation:a multi-objective approach［J］.Transportation Res:Part E，2009，45(6):878-892.

［7］王军，李卓蓉.基于遗传算法的动态泊位分配问题优化研究［J］.中国水运，2011，11(1):63-65.

［8］何军良，宓为建，谢尘，等.基于分布式混合遗传算法的动态泊位分配策略与仿真［J］.上海海事大学学报，2008，29(2):53-57.

［9］曾庆成，张倩.集装箱泊位分配干扰管理仿真优化模型与算法［J］.中国科技论文在线，2009，4(10):742-746.

［10］王红湘，严伟.基于启发式算法和仿真优化的岸壁线长度泊位分配策略［J］.上海海事大学学报，2008，29(1):19-22.

［11］张静，刘翠莲.港口泊位服务系统的影响因素及其仿真［J］.大连海事大学学报:社会科学版，2008，7(6):110-112.

［12］沙梅.集装箱码头物流系统建模与仿真综述［J］.上海海事大学学报，2005，26(1):6-12.

［13］马小姝，李宇龙，严浪.传统多目标优化方法和多目标遗传算法的比较综述［J］.电气传动自动化，2010，32(3):48-50.