无轴承开关磁阻电机缺相运行的控制方法
2013-07-06邓智泉赵丽丹
邓 旭 邓智泉 曹 鑫 赵丽丹 钱 婷
(南京航空航天大学航空电源航空科技重点实验室 南京 210016)
1 引言
无轴承开关磁阻电机(Bearingless Switched Reluctance Motor,BSRM)是利用磁轴承与电机结构的相似性,将磁轴承中的悬浮绕组叠绕在开关磁阻电机(Switched Reluctance Motor,SRM)定子上,通过电力电子和微机控制使其同时具备驱动和磁悬浮支撑功能的一种新型磁悬浮电机。BSRM 除了拥有SRM 固有的优势外,还解决了电机长时间高速运行所带来的轴承维护和保养难题[1-6],在航空航天、高速和极端条件下具有重要应用特色[13-15]。
在电机容错方面,传统 SRM的研究成果对BSRM 有重要的参考意义。从20 世纪90年代开始,各国学者对SRM 本体和功率变换器容错进行了深入的研究。目前,关于SRM的容错研究已从正常运行和容错运行的性能对比转变为对电流控制器的优化以及缺相条件下的转矩补偿策略,并关注于减小转矩脉动和尖峰电流。此外,部分学者将研究重点放在SRM 系统中功率变换器的断路和短路故障检测上,完善了整个系统的容错性能[7-11]。
由BSRM的结构可知,常见的缺相故障包括主绕组断路、悬浮绕组断路和两者同时断路。这三种故障都将导致悬浮力缺失,需要对其进行补偿,不同的是前两种故障发生时,同相悬浮绕组或主绕组依旧能够正常开通提供正向转矩。因此,从输出转矩角度而言,主绕组和悬浮绕组同时断路故障对BSRM 运行的稳定运行影响更大,因此,本文将主要针对此故障下 BSRM的悬浮和旋转控制展开研究,通过提出悬浮力和转矩补偿策略解决了BSRM在缺相运行下的稳定悬浮和转矩补偿。
2 电机结构及全角度数学模型
本文以一台三相12/8 极BSRM 为研究对象,电机A 相绕组结构如图1 所示。文献[5,6,11,12]推导了电机单相导通的数学模型,以A 相绕组为例,悬浮力和转矩为

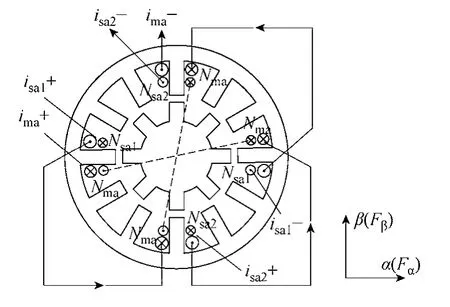
图1 A 相绕组结构示意图Fig.1 Configuration of phase A winding
J(θ)在电感上升区域可以表示为

Jt(θ)在电感下降区域可以表示为

式中Fα,Fβ——α和β方向瞬时悬浮力;
Nm,Ns——任一定子极的主绕组和悬浮绕组匝数;
ima,isa1,isa2——A 相主绕组电流和α、β方向的悬浮绕组电流;
Kf——悬浮力系数;
Jt——转矩系数;
其中Kf,Jt均为关于转子位置角θ的函数。
3 缺相控制策略
在主绕组断路故障中,为保证转子悬浮,缺失的悬浮力需由上一相主绕组和悬浮绕组同时延长导通区间进行补偿。设电机旋转相序为A—B—C,各相轮流导通15°。若C 相主绕组断路,则悬浮力补偿方法下的电流分布如图2 所示。C 相缺失的悬浮力由B 相延长导通15°提供,从而保证了转子在完整的电感周期内的连续悬浮。但是,由于延长导通区间位于B 相的负转矩区,从而导致电机的输出转矩进一步减小为正常运行时的1/3。根据式(2)可推导出平均转矩表达式为

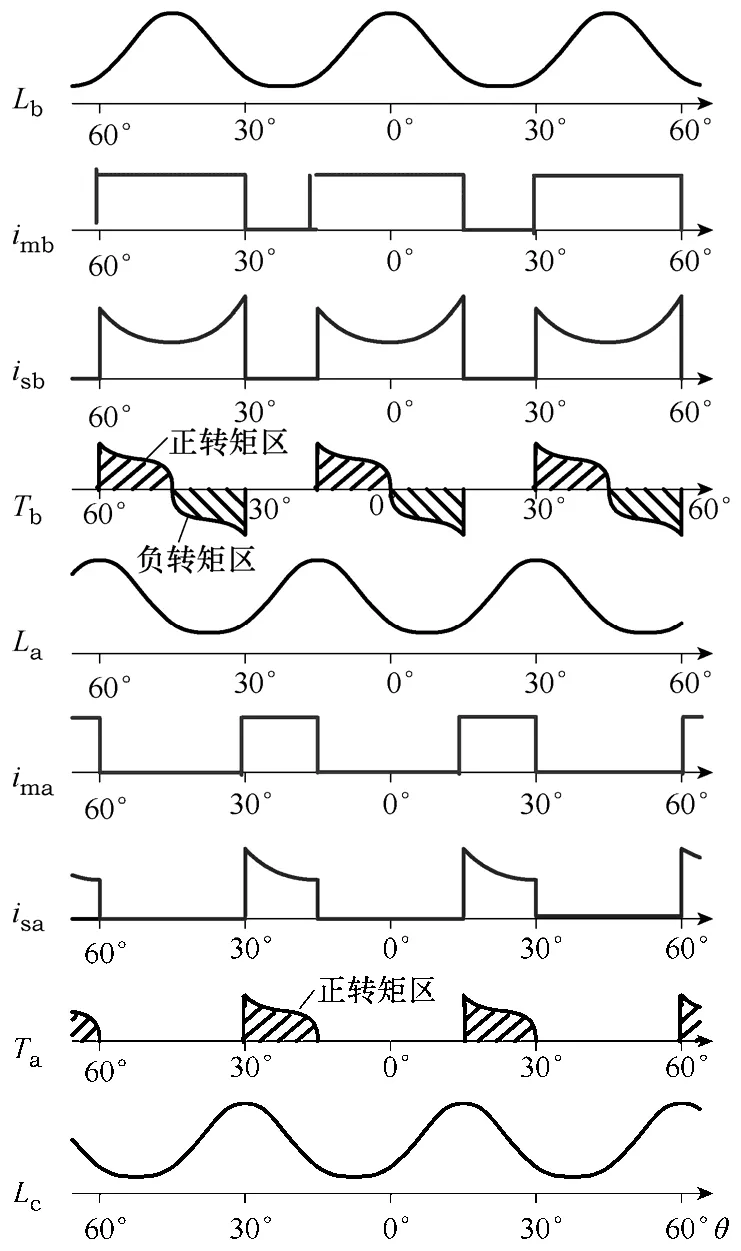
图2 悬浮力补偿策略Fig.2 Compensation strategy of levitation force
式中im,is1,is2——导通相的主绕组电流和α、β 方向的悬浮绕组电流。
图3 为提前开通策略电流导通示意图,此策略在悬浮力补偿策略的基础上,将正常相A 相和B 相的主绕组提前开通,从而产生更多的正转矩以增加缺相运行时的输出转矩。其平均转矩表达式为

式中θon——主绕组开通角。

图3 提前开通策略Fig.3 Compensation strategy of turn-on in advance
采用悬浮力补偿策略时,B 相悬浮电流在正、负转矩区对称导通,虽补偿了缺失的C 相悬浮力,但转矩损失严重。因此,在保证提供相同悬浮力的前提下,应尽量减小补偿相在负转矩区[0,15°]内产生的瞬时转矩,达到提高平均转矩的目的。参考文献[7]提出的独立控制策略,图4 为电流优化策略导通示意图。

图4 电流优化策略Fig.4 Compensation strategy of current optimization
令电机径向合成力F为

则合成力F和瞬时转矩T可表示如下:

根据瞬时转矩T的表达式,有如下不等式成立
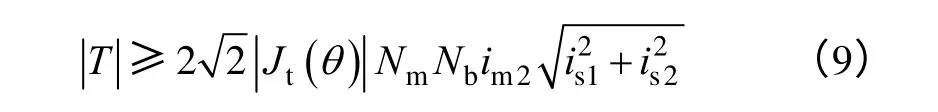
当取最小值时,有

因此,在[0,15°]内产生的最小负转矩的主绕组电流im2可表示为

则平均转矩表达式为

式中is12,is22——电流优化区间内α、β方向的悬 浮绕组电流。
图5 为BSRM的缺相控制框图。通过光电传感器检测出转子位置后经位置解算得到电机的实时转速,其与给定转速的差值经PI 调节器输出为主绕组 电流。两个径向位移经电涡流传感器转换为电信号,经PID 调节器输出为悬浮力给定值和。根据测量值,通过缺相下电流优化算法解算出优化区间内的主绕组电流和悬浮绕组电流和。最后,通过两套绕组的功率控制器实时跟踪电流给定值,以实现电机运行时的稳定悬浮。

图5 缺相系统控制框图Fig.5 Control diagram of open-phase operation
4 仿真分析
根据提出的缺相控制算法,通过有限元仿真验证其有效性。仿真模型采用实验样机参数见下表。

表 样机参数Tab. Parameters of the test motor
如图6 所示,在绕组电流与母线电压均恒定的情况下,随着开通角从-15°变化到-22.5°,电机转速从1 325r/min 增加到1 550r/min,理论计算和有限元仿真结果基本吻合。由图可知,开通角越前,转矩的补偿趋势越小,在-20°之前补偿不再明显。因此利用提前开通策略时,开通角选取在[-20°,-15°]之内是合适的。

图6 开通角与转速关系(ima=6A、isa1=4A、isa2=2A)Fig.6 Relationship between turn-on angle and speed
为验证电流优化策略的有效性,本文通过有限元仿真分析产生相同悬浮力的不同电流产生的瞬时负转矩分布曲线。图7 中采用了三组不同的电流值,一组是经过电流优化算法得到的值,另两组是不同的恒定电流值。由图可见,在保证产生相同悬浮力的情况下,经过优化后的电流产生的瞬时负转矩最小,因此该算法能够有效减小负转矩。

图7 优化电流与恒值电流产生的转矩比较Fig.7 Torque comparison of optimized current and constant currents
图8 所示为正常运行与缺相下一个旋转周期内的悬浮力、转矩以及电流的分布对比。其中,A 相的定、转子齿极对齐位置定义为θa=0°,径向力给定值分别为30N 和60N。由图8b 可知,悬浮力补偿策略可以提供稳定的悬浮力。由图8c 可知,缺相运行下由于采用了提前开通策略和电流优化策略,转矩脉动、瞬时负转矩和悬浮绕组电流平均值都得到了有效控制。

图8 一个旋转周期内的悬浮力、转矩以及电流的分布Fig.8 Levitation force,torque and current distribution in a rotation period
5 实验结果与分析
本文对所提出的BSRM 缺相运行控制方法进行了实验验证,实验样机结构参数见上面表。图9 所示为样机的实物照片,其中转速信号由光电传感器获得。由于转子重力的影响,近似于对电机转子在β方向施加了一个5kg的径向负载。

图9 电机外观图Fig.9 Photograph of the test motor
本文分别实现了提前开通策略下和电流优化策略下的稳定悬浮。图10~图12 分别为正常运行、提前开通策略下和电流优化策略下稳定悬浮时的电流波形。由图可见,在缺相情况下,利用提前开通策略时,为了达到与正常运行相同的转速,主绕组和悬浮绕组电流都相应地增大,而采用电流优化控制策略之后,主绕组电流的平均值明显减小。


图10 正常运行的电流波形(图中电流均为6.66A/格)Fig.10 Current waveforms of normal operation


图11 采用提前开通策略的电流波形(图中电流均为6.66A/格)Fig.11 Current waveforms of opening in advance strategy

图12 采用电流优化策略的电流波形(图中电流均为6.66A/格)Fig.12 Current waveforms of current optimization strategy
图13 为样机缺相下的两种控制策略对应的悬浮波形和正常运行时的悬浮波形,可以看出缺相下的悬浮精度和正常运行基本持平,说明提前开通策略和电流优化策略都能保证电机良好的悬浮性能。

图13 悬浮波形Fig.13 Levitation waveforms
为测试电机缺相时的工作性能,进行了径向敲击实验和升速试验。径向敲击实验波形如图14 所示,α和β方向的位移由于敲击而分别偏离中心位置,此时悬浮绕组电流增大,从而使转轴被迅速拉回几何中心。需要指出的是:由于木槌敲击转轴时无法保证精确地穿过转轴几何中心,图14 中的两组波形在非干扰方向也存在较小波动,但电机仍能迅速恢复稳定悬浮。由此可见,缺相运行具有良好的抗干扰能力。

图14 径向力突变实验波形Fig.14 Waveforms of radial force disturbance
图 15 所示为电机升速实验波形。在转速从1 500r/min 升高到2 000r/min的过程中,转轴的径向位移波形与转速恒定时保持一致,而悬浮绕组电流波形在升速过程中也基本保持稳定,说明提前开通策略在转速变化过程中能够保持良好的悬浮性能。
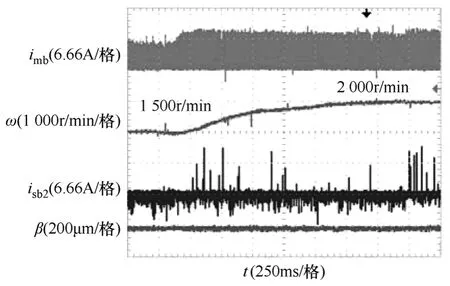
图15 电机升速实验波形Fig.15 Waveforms of step acceleration with the new control strategy
6 结论
本文研究了无轴承开关磁阻电机的缺相运行及其控制方法。提出了悬浮力补偿策略和两种转矩补偿策略,实现了无轴承开关磁阻电机的缺相悬浮,得到如下结论:
(1)悬浮力补偿策略能够保证电机的稳定悬浮,提前开通策略能有效补偿缺相带来的转矩缺失;与此同时,电流优化策略也能有效提高平均转矩幅值。
(2)与正常运行相比,缺相运行仍能保持良好的悬浮精度和动态性能。
[1]Takemoto M,Shimada K,Chiba A,et al.A design and characteristics of switched reluctance type bearingless motors[C].Fourth International Symposium on Magnetic Suspension Technology,Gifu,Japan,1998:49-63.
[2]Amrhein W,Silber S,Nenninger K.Developments on bearingless drive technology[C].8th International Symposium on Magnetic Bearings,Mito,Japan,2002:343-348.
[3]Takemoto M,Chiba A,Fukao T.A feed-forward compensator for vibration reduction considering magnetic attraction force in bearingless switched reluctance motors[C].7th International Symposium on Magnetic Bearings,ETH Zurich,2000:395-400.
[4]Choi B B,Siebert M.A bearingless switched reluctance motor for high specific power applications[C].42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit,Sacramento,CA,2006:4804-4810.
[5]杨钢.无轴承开关磁阻电动机的基础研究[D].南京:南京航空航天大学,2008.
[6]曹鑫.12/8 极无轴承开关磁阻电机的研究[D].南京:南京航空航天大学,2010.
[7]Cao X,Deng Z,Yang G,et al.Independent control of average torque and radial force in bearingless switched-reluctance motors with hybrid excitations[J].IEEE Trans.on Power Electronics,2009,24(5):1376-1385.
[8]Arkada A A,Sidani M,Du P.Characterization of SRM drive systems under normal and fault operating condition[C].International Conference LMED,1999:249-251.
[9]Gameiro N S,Cardoso A J M.Fault tolerant control strategy of srm drives[C].International Symposium on Power Electronics,Electrical Drives,Automation and Motion,2008:301-306.
[10]Gameiro N S,Cardoso A J M.Power converter fault diagnosis in SRM drives based on the DC bus current analysis[C].International Conference on Electrical Machines(ICEM),2010:1-6.
[11]Mir S,Islam M S,Sebastian T,et al.Fault-tolerant switched reluctance motor drive using adaptive fuzzy logic controller[J].IEEE Trans.on Power Electronics,2004,19(2):289-295.
[12]邓智泉,杨钢,张媛,等.一种新型的无轴承开关磁阻电机数学模型[J].中国电机工程学报,2005,25(9):139-146.Deng Zhiquan,Yang Gang,Zhang Yuan,et al.An innovative mathematical model for a bearingless switched reluctance motor[J].Proceedings of the CSEE,2005,25(9):139-146.
[13]Ooshima M,Takeuchi C.Magnetic suspension performance of a bearingless brushless dc motor for small liquid pumps[J].Electrical Machines and Systems,2009,47(1):72-78.
[14]Asama J,Fukao T,Chiba A,et al.A design consideration of a novel bearingless disk motor for artificial hearts[C].Energy Conversion Congress and Exposition,2009:1693-1699.
[15]Zhou J,Tseng K J.A disk-type bearingless motor for use as satellite momentum-reaction wheel[C].IEEE 33rd Annual Power Electronics Specialists Conference,2002:4(s):1971-1975.
