考虑偏心及绕组耦合的无轴承永磁同步电机建模

孙晓东 陈 龙 杨泽斌 朱秋 左文全 施 凯

（1．江苏大学汽车工程研究院 镇江 212013 2.江苏大学电气信息工程学院 镇江 212013）

1 引言

磁轴承是近三十年发展起来的一种新型高性能轴承，具有无摩擦、无磨损、不需润滑及密封、高速度、高精度及寿命长等优点，已在能源交通、机械加工工业、航空航天及机器人等领域获得了实际应用[1,2]。然而由于磁轴承体积及激励功率大，导致磁轴承支承的电机结构尺寸和成本增大，临界转速降低，使其在大功率和微型应用场合受限制。无轴承电机是依据磁轴承和传统交流电机结构的相似性，将磁轴承技术和电机相结合提出的一种新型特种电机。与磁轴承支承的电机相比，无轴承电机尺寸小、功率密度高，能同时实现高转速和大功率，因此无轴承电机具有比磁轴承更广阔的应用前景。

无轴承电机的种类很多，其中结构简单、运行可靠、 功率密度大的无轴承永磁同步电机（BPMSM）受到了高度重视[3-13]。BPMSM 是在传统永磁同步电机的定子上增加了一套悬浮力绕组，其激励的悬浮力绕组气隙磁场与原有的永磁同步电机的气隙磁场（永磁体激励的磁场与转矩绕组激励的磁场，这两部分磁场合称为“转矩绕组气隙磁场”）相叠加。通过调节悬浮力绕组电流以改变气隙磁场的分布，利用转子一对极两侧的气隙磁场不平衡作用产生的作用于转子上的径向悬浮力，实现转子的稳定悬浮。

BPMSM 本体的设计和控制策略的研究、设计及分析都需要以准确的数学模型为理论依据，因此数学模型的研究一直受到相关学者的关注。BPMSM两套绕组共同作用产生径向悬浮力，电磁转矩和径向悬浮力之间，以及径向两自由度悬浮力之间存在耦合关系，而且BPMSM 实际运行过程中还存在定转子偏心，使得BPMSM 相对于传统的永磁同步电机而言，是一个更为复杂的非线性、强耦合系统，这就给BPMSM的数学建模增加了难度。

文献[5]通过实验方法确定了表面贴装式BPMSM的电感系数，进而利用虚位移方法确定了BPMSM 径向悬浮力模型，该方法所用参数需要通过实验测得，计算量较大，而且实验测量容易引起较大的误差，文献[6,7]分别对插入式、埋入式BPMSM 做了深入研究，由转矩绕组与悬浮力绕组交链的磁链方程得出电磁能数学表达式，再对该电磁能表达式求偏导得出转子受到的径向悬浮力表达式，文献[8]研究了具有4 极转矩绕组和2 极悬浮力绕组的无轴承电机通用可控径向悬浮力解析模型，分别对凸极型无轴承同步磁阻电机、圆柱形无轴承异步电机和表面贴装式 BPMSM 进行对比研究，并进行了径向悬浮力的静力实验和分析，验证了通用可控径向悬浮力解析模型的有效性和正确性，文献[5-8]对BPMSM 数学模型的研究仅仅停留在径向悬浮力上，并未涉及电机的电磁转矩方程，而且对定转子偏心情况下的径向悬浮力与电磁转矩之间的影响没有展开研究。文献[9]利用机械/电气坐标系变换建立了 BPMSM 转矩绕组与悬浮力绕组的磁链与电压方程，通过分析BPMSM 内的各部分洛仑兹力确定了电磁转矩方程，在分析BPMSM 各部分径向悬浮力数学表达形式的基础上，得出BPMSM 径向悬浮力方程的完整形式。该方法建模概念清晰、简单直观、易于理解，但是并未将转矩方程与径向悬浮力方程统一起来，没有考虑两者之间的耦合关系。

本文首先介绍了BPMSM的径向悬浮力产生原理，针对无轴承电机相关电感参数难以准确实验测量，从而难以得到径向悬浮力和电磁转矩较为准确的数学模型的问题，根据电机磁路原理，用解析法推导出BPMSM各电感参数较为准确的解析计算模型，并基于此电感模型推导出BPMSM的径向悬浮力和电磁转矩的解析模型。由于该方法充分考虑了定转子偏心状况时径向悬浮力与电磁转矩之间的耦合关系，因此采用该方法后，BPMSM系统的静、动态性能得到显著改善。最后在一台表面贴装式BPMSM实验样机上进行了实验研究，实验结果验证了该数学模型的优良特性。

2 BPMSM 径向悬浮力产生原理

当BPMSM转矩绕组极对数pM=1，且悬浮力绕组极对数pB=2时，BPMSM径向悬浮力产生原理如图1所示，四极悬浮力绕组NBα和NBβ与二极转矩绕组NMα和NMβ一起叠压在定子槽内，通过悬浮力绕组电流所产生的四极磁通ψ4打破二极气隙磁通ψ2的平衡来产生径向悬浮力。当转子位于中心位置时，对称的二极磁通ψ2由永磁体产生，电机在空载运行时，转矩绕组电流产生的磁通比较小，可以忽略不计。如果NBα和NBβ中不通入电流，ψ2是平衡的，不产生径向悬浮力。当NBα中通入正向电流之后，产生的ψ4如图1a所示，导致在转子右侧气隙1处的磁密增强，转子左侧气隙3处的磁密减弱，产生沿α轴正方向的径向悬浮力，从而使转子向α轴正方向偏移；如果NBα中通入相反方向的电流，则会产生一个沿α轴负方向的径向悬浮力。同理，图1b为β方向的径向悬浮力产生原理图，绕组NBβ与NBα在电气坐标系中互相垂直，当NBβ中通入正向电流之后，产生的ψ4打破了ψ2的平衡，导致在气隙1′和气隙2′处的磁密增强，而气隙3′和气隙4′处的磁密减弱，产生沿β轴正方向的径向悬浮力，从而使转子向β轴正方向偏移；如果NBβ中通入相反方向的电流，则会产生一个沿β轴负方向的径向悬浮力。因此，通过控制悬浮力绕组NBα和NBβ中的电流就可以控制径向悬浮力的大小和方向，从而实现转子的稳定悬浮。

图1 径向悬浮力产生示意图Fig.1 Producing principles of radial suspension forces

3 BPMSM 电感矩阵模型

实际BPMSM 中绕组为三相，由于三相绕组经3/2 变换可等效为两相绕组，为简便计，本文以两相等效绕组为例进行推导。α-β坐标系为静止直角坐标系，其坐标原点位于定子中心线上。图 2 为BPMSM 定转子产生偏心时的示意图。转子外表面和定子内表面之间的气隙长度g(θ)可以写为转子在α和β方向上的偏心距离。设图中O′(α，β)为偏心转子轴心的坐标；R为定子内半径；r为转子外半径；g0为单边平均气隙长度；Δg为偏心气隙长度，从而g(θ)可表示为

式中θ——沿定子内表面逆时针机械角度；

α，β——转子沿α、β方向的径向位移。

图2 转子偏心示意图Fig.2 Sketch of rotor eccentricity

考虑到BPMSM 在悬浮运行过程中，转子偏心位移一般远小于电机的单边平均气隙长度，故转子偏心的平方项(Δg)2可忽略不计，则气隙长度倒数可表示为

则作用在圆周 dθ弧度内的气隙磁导分布函数为

式中μ0——空气磁导率；

l——转子铁心有效长度。

在图1 中，定义转矩绕组和悬浮力绕组的a 相绕组轴线重合且位于α轴线上。转矩绕组每相串联有效匝数为WM，悬浮力绕组每相串联有效匝数为WB，在等效原则下，假设各绕组为整距集中绕组，则绕组沿气隙的分布为一周期性矩形波。通过傅里叶分解，可将周期性矩形波分解为基波和一系列奇次谐波，这里只考虑基波绕组，此时基波绕组在空间按正弦规律分布，其中基波的幅值为矩形波幅值的4/π，记为K，则各绕组沿气隙圆周的匝数分布规律可表示为

如果BPMSM 空载运行，则各相正弦绕组（或等效正弦绕组）中流过的对称正弦电流为

式中iMa，iMb——转矩绕组电流α轴与β轴分量（包括转子永磁体激励的磁场等效至转矩绕组中的电流部分）；

iBa，iBb——悬浮力绕组电流α轴与β轴分量；

若忽略电机铁心磁路压降以及铁心磁饱和的影响，则沿定子内表面dθ弧度内的气隙磁通量dφMa(θ)可以表示为（以a 相为例）

式中VMa——由转子偏心所产生的转子磁位偏移。

根据高斯定律，气隙磁通量dφMa(θ)沿气隙圆周的积分为零，则可以计算出转子偏心引起的转子磁位VMa表达式为

同理可以计算出

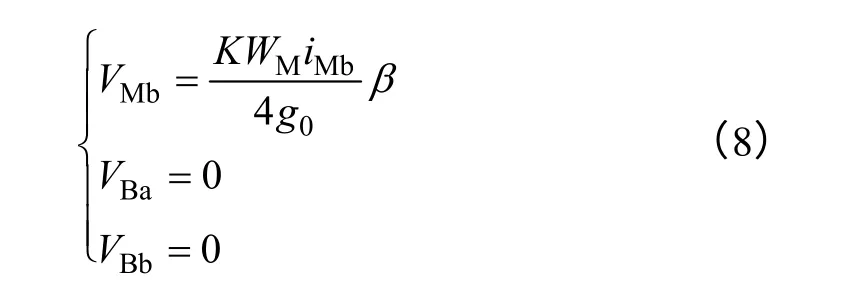
则BPMSM 在电机转子外表面dθ弧度内产生的各相气隙磁通变化规律为

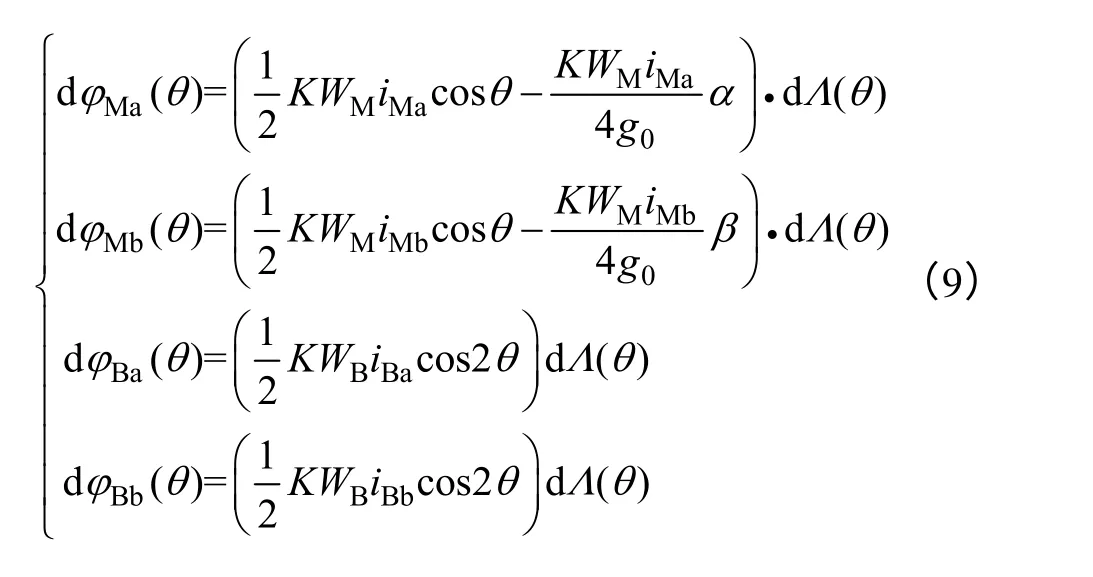
根据磁链和电流的关系，可定义出BPMSM的转矩绕组自感矩阵LM、悬浮力绕组自感矩阵LB以及两套之间的互感矩阵M分别为

将式（4）、式（5）、式（9）代入式（10），对各电感矩阵参数进行计算，得到电感矩阵模型为

式中LM，LB——转矩绕组和悬浮力绕组的自感系数，

M——两套绕组的互感系数，且

4 BPMSM 数学模型

4.1 径向悬浮力方程

由于电机的磁场储能反映为绕组激磁电流在绕组电感中的储能，如果忽略电机磁路饱和与铁心磁压降，则电机气隙磁场储能Wm可表示为

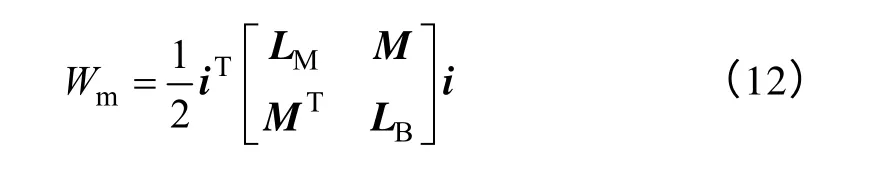
式中i——两相静止坐标系下的电流矢量，

根据虚位移原理，径向悬浮力可表示为电磁能Wm对位移的偏导，对式（12）求偏导，得到的α、β方向上的径向悬浮力为

用式（5）中的iMa与iMb代入，此时式（13）可表示为

对于悬浮力绕组电流矢量控制，若采用以下PARK 逆变换公式

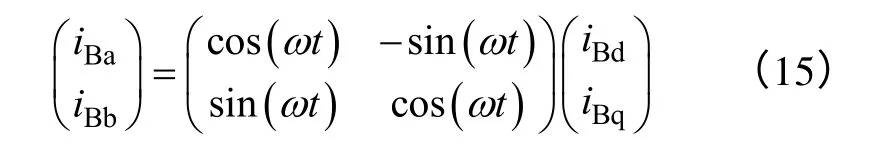
式中iBd，iBq——悬浮力绕组电流在两相旋转坐标系下的d 轴与q 轴分量。

则式（14）变为

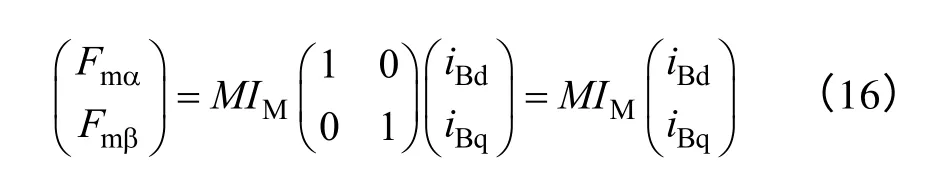
式中If——转子永磁体激励的磁场等效至转矩绕 组中的电流部分；

iMd，iMq——转矩绕组电流在两相旋转坐标系下的

d 轴与q 轴分量；

另外，BPMSM 转子受到的径向悬浮力还包括由于转子偏心引起气隙磁场分布不均而产生的径向悬浮力。这部分径向悬浮力随转子偏心程度的增加而增大，而且两者之间成正比例关系，比例系数与转矩绕组电流平方成正比例关系[14]。由电机气隙磁场的均匀性与对称性可知，这种正比例关系在α、β方向上是等同的。该部分径向悬浮力可表示为

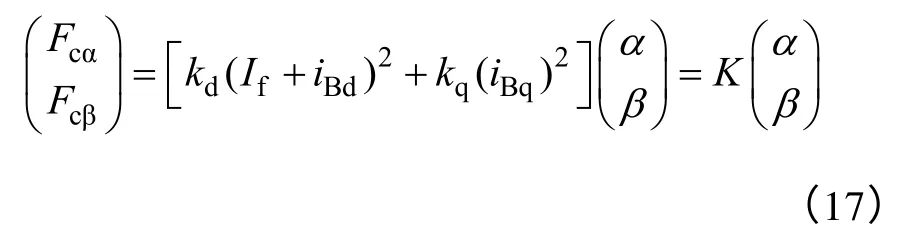
式中，K=kd+kq，kd与kq均为常数。

综合式（16）与式（17），得到BPMSM的径向悬浮力方程为

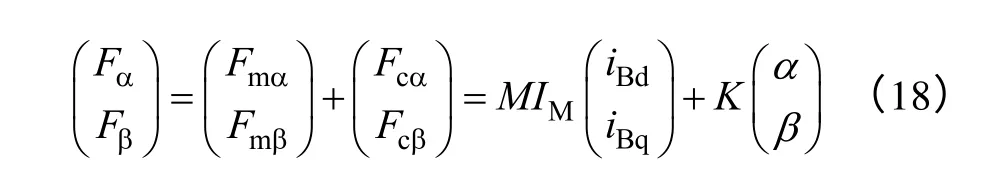
4.2 电磁转矩方程

由于负载变化、外在干扰以及径向位移检测误差，将会导致BPMSM 悬浮运行时定转子中心并不重合，总是存在偏心，因此转矩绕组和悬浮力绕组之间存在大小随转子位移成正比变化的互感，此时电磁转矩与径向悬浮力之间的耦合关系更加复杂，故必须考虑悬浮力绕组对电磁转矩的影响。在两相旋转坐标系下，转矩绕组和悬浮力绕组的电流可以表示为如下矢量形式

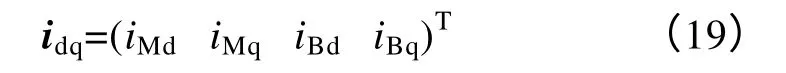
则式（12）表示的电机气隙磁场储能Wm可改写为

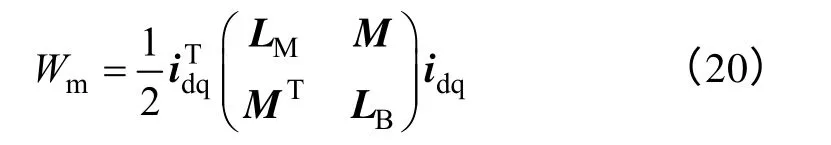
根据虚位移原理，电磁转矩可表示为电磁能Wm对转子位置角的偏导，因此电磁转矩方程为[15]

由式（21）可以看出，当考虑定转子偏心情况时，除了第1 项为转子永磁体等效励磁电流与转矩绕组电流相互作用产生的电磁转矩，与传统表面贴装式永磁同步电机电磁转矩公式相同外，后面4 项体现了悬浮力绕组对电磁转矩产生的影响。

5 实验验证

本文以一台表面贴装式BPMSM 为实验样机进行了实验研究。实验样机参数如下：功率1kW，定子外径130mm，定子内径69mm，转子外径67mm，永磁体厚度2mm，电机气隙2mm，36 槽，电机转矩绕组电阻2.01Ω，直轴和交轴电感0.008H，悬浮力绕组电阻1.03 Ω，直轴和交轴电感0.003H，两套绕组互感为0.000 16H，转动惯量0.007 69kg·m2，辅助机械轴承气隙为0.5mm。

为了验证本文模型推导的正确性，以转矩绕组为例，将转矩绕组交直轴电感的理论计算值与测量值进行了比较，结果见下表。从表可以看出，理论值与测量值十分接近。

表 转矩绕组交直轴电感的理论值与测量值比较Tab. Comparison between measured inductance and theoretical one(dq-axis)of torque windings

当转矩绕组采用iMd=0的矢量控制时，转矩绕组的表达式可以表示为

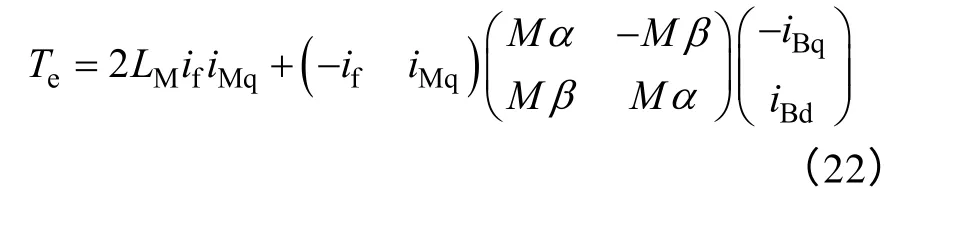
此时相应的BPMSM 矢量控制框图如图3 所示。

图3 BPMSM 控制系统框图Fig.3 Control system block diagram of the BPMSM

为了验证本文所提出建模方法的有效性，对采用本文模型（简称为新模型）及未采用本文模型（简称为原模型）两种情况进行了实验研究，其中原模型的具体建模过程可参考文献[16]，并且两种模型均是采用iMd=0的矢量控制，图4 和5 所示分别为采用原模型和新模型时实验样机的稳、动态实验波形。其中，图4a 和5a 为实验样机在转速恒定为1 200r/min 时，电机的径向位移波形，从上向下依次为α、β方向上径向位移。图4b 和5b 为α与β方向上径向位移关系波形，图4c 和5c 为实验样机从600r/min 升速到1 200r/min 时的动态过程试验波形，图4d 和5d 为转速变化过程中转子α方向径向位移的动态变化曲线。

从图4a 和5a，及图4b 和5b的比较可知，转子在α、β方向上总的位移幅值范围减小，稳态悬浮精度由原来的±40μm 左右提高到±35μm 左右，峰-峰值从原来的小于80μm，提高到小于70μm；从图4c 和5c 比较，及图4d 和5d 比较可知，实验样机从600r/min 动态升速到1 200r/min 所需的时间由原来的1.6s 缩短到0.8s。这说明，采用本文模型时有效地提高了电机悬浮运行时的稳态精度和动态响应速度，实验样机的动、稳态试验结果表明了本文研究方法的可行性和有效性。

图4 原模型稳态和动态实验波形Fig.4 Static and dynamic waveforms of previous model

图5 新模型稳态和动态实验波形Fig.5 Static and dynamic waveforms of new model

6 结论

根据电机磁路原理，详细分析推导出了BPMSM 电感系数和电感矩阵解析计算模型，并基于该电感矩阵模型和电机电磁场虚位移原理，建立BPMSM 径向悬浮力和电磁转矩的计算公式。充分考虑了在定转子偏心情况下，悬浮力绕组对电磁转矩的耦合影响，为电机运行状态的分析和无轴承电机的本体设计提供了可靠的理论依据。实验分析结果表明，利用该模型能更好的实现电机在稳、动态场合下的稳定悬浮运行，从而为BPMSM 走向实用化提供了一种有效手段。

[1]Greatrex N A,Timms D L,Kurita N,et al.Axial magnetic bearing development for the BiVACOR rotary BiVAD/TAH[J].IEEE Transactions on Biomedical Engineering,2010,57(3):714-721.

[2]Hijikata K,Takemoto M,Ogasawara S,et al.Behavior of a novel thrust magnetic bearing with a cylindrical rotor on high speed rotation[J].IEEE Transactions on Magnetics,2009,45(10):4617-4620.

[3]Sun X,Zhu H.Study on static electromagnetic characteristics of a bearingless permanent magnet synchronous motor[J].Advanced Science Letters,2012,5(1):40-48.

[4]Zhang S,Luo F L.Direct control of radial displacement for bearingless permanent-magnet-type synchronous motors[J].IEEE Transactions on Industrial Electronics,2009,56(2):542-552.

[5]Oshima M,Miyazawa S,Deido T,et al.Characteristics of a permanent magnet type bearingless motor[J].IEEE Transacitons on Industry Application,1996,32(2):363-370.

[6]Inagaki K,Chiba A,Rahman M A,et al.Performance characteristics of inset-type permanent magnet bearingless motor drives[C].Proceedings of Power Engineering Society Winter Meeting,Singapore,2000,1:202-207.

[7]Ooshima M,Yamashita K,Chiba A,et al.An improved control method of buried-type IPM bearingless motors considering magnetic saturation and magnetic pull variation[C].Proceedings of IEEE International Electric Machines and Drives Conference,Madison,US,2003,1:1055-1060.

[8]卜文绍,万山明,黄声华,等.无轴承电机的通用可控磁悬浮力解析模型[J].中国电机工程学报,2009,29(30):84-89.Bu Wenshao,Wan Shanming,Huang Shenghua,et al.General analytical model about controllable magnetic suspension force of bearingless motor[J].Proceedings of the CSEE,2009,29(30):84-89.

[9]Zhu H,Cheng Q,Wang C.Modeling of bearingless permanent magnet synchronous motor based on mechanical to electrical coordinates transformation[J].Science in China,Series E:Technological Sciences,2009,52(12):3736-3744.

[10]Yamada T,Nakano Y,Asama J,et al.Outer Rotor Consequent-Pole Bearingless Motor With Improved Start-Up Characteristics[J].IEEE Transactions on Magnetics,2008,44(11):4273-4276.

[11]Nussbaumer T,Karutz P,Zurcher F,et al.Magnetically levitated slice motors-an overview[J].IEEE Transactions on Industry Applications,2011,47(2）:754-766.

[12]Zhu H,Cheng Q.Bearingless motor’s radial suspension force control based on flux equivalent with virtual winding current analysis method[J].Chinese Science Bulletin,2009,54(9):1590-1598.

[13]Cao X,Deng Z.A full-period generating mode for bearingless switched reluctance generators[J].IEEE Transactions on Applied Superconductivity,2010,20(3):1072-1076.

[14]Ooshima M,Kurokawa T,Sakagami M,et al.An identification method of suspension force and magnetic unbalance pull force parameters in buried-type IPM bearingless motors[C].Proceedings of Power Engineering Society General Meeting,Denver,USA,2004,1:1276-1279.

[15]Amrhein W,Silber S,Nenninger K.Levitation forces in bearingless permanent magnet motors[J].IEEE Transactions on Magnetics,1999,35(5):4052-4054.

[16]朱熀秋,巫亮,周阳,等.无轴承永磁同步电机转子磁场定向控制系统研究[J].中国工程科学,2006,8(6):35-40.Zhu Huangqiu,Wu Liang,Zhou Yang,et al.The research on rotor magnetic flux oriented control system for bearingless permanent magnet synchronous motor[J].Engineering Science,2006,8(6):35-40.