共振情形下四点泛函边值问题解的存在性
2013-07-05杜睿娟
杜睿娟
(甘肃政法学院计算机科学学院,甘肃兰州 730070)
共振情形下四点泛函边值问题解的存在性
杜睿娟
(甘肃政法学院计算机科学学院,甘肃兰州 730070)
运用Mawhin重合度理论,讨论了一类二阶四点泛函边值问题解的存在性和多解性.分别在非线性项f有界和无界的条件下,获得了此类泛函边值问题解的存在性结果.
泛函边值问题;存在性;Caratheodory条件;共振
1 引言
微分方程多点边值问题在经济学、人口动力学、生态学等方面有着广泛的应用,例如动物血红细胞存在模型、人口动力系统模型等.因此,对微分方程边值问题解存在性的研究就更具有现实意义.近年来,诸多学者对微分方程边值问题解的存在性进行了深入的研究,并取得了丰富的研究成果[1-5].特别地,文献[6]讨论了如下非线性二阶四点微分方程边值问题:

解的存在性.显然,上述非线性项仅与x,x′有关,而不依赖于x,x′的函数F(x),G(x′).因此,自然地,当非线性项不仅与x,x′有关,而且还依赖于x,x′的函数F(x),G(x′)时,上述微分方程边值问题的解是否仍然存在?基于此,本文讨论了如下共振情形下二阶四点泛函边值问题:
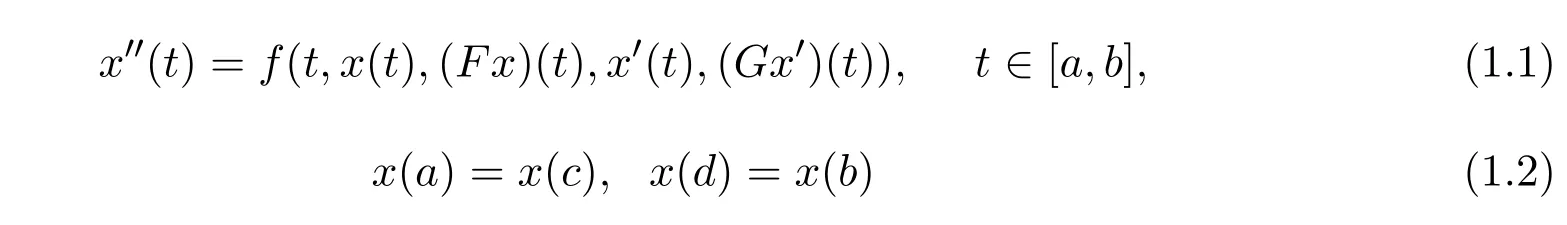
解的存在性,其中a,b,c,d∈R,a<c≤d<b,f:[a,b]×R4→R满足Caratheodory条件, F,G∈D,D为全体连续有界算子.得到了上述边值问题有解以及多解的充分条件,丰富了多点泛函边值问题解的存在性理论.本文用到的非线性工具为Mawhin[7]重合度理论.
2 预备知识

3 非线性项f有界情形下解的存在性





4 非线性项f无界情形下解的存在性


[1]Zhang G,Sun J.Positive solutions of m-point boundary value problems[J].J.Math.Anal.Appl.,2004,29(1): 406-418.
[2]Padhi S,Shilpee Srivastava.Multiple periodic solutions for nonlinear first order functional differential equations with applications to population dynamics[J].Appl.Math.Comput.,2008,203(1):1-6.
[3]An Y.Existence of solution for a three-point boundary problem at resonance[J].Non.Anal.,2006,65(3):1633-1643.
[4]莫宜春,孙晋易,王珍燕.一类泛函微分方程半正问题的正周期解[J].纯粹数学与应用数学,2012,28(1):137-143.
[5]姚庆六.线性增长限制下一类三阶边值问题的可解性[J].纯粹数学与应用数学,2005,21(2):164-167.
[6]Rachunkove,Stanek.Topological degree method in functional boundary value problems at resonance[J]. Nonlinear Anal.,1996,27:271-285.
[7]Mawhin J.Topological degree methods in nonlinear boundary value problems[C]//NSF-CBMS Regional Conference series in Mathematics.Providence R I:American Mathematical Society,1997.
Solvability of functional differential equations with four-point boundary value problem at resonance
Du Ruijuan
(Department of Computer Science,Gansu Political Science and Law Institute,Lanzhou730070,China)
In this paper,by using Mawhin coincidence degree theorem,we study the solvability and multiplicity of the seconder-order functional differential equations with four-point boundary value problems at resonance. Under the conditions of boundary and unboundary of the nonlinearity f respectively,the existence of solution for the above functional boundary value problems are obtained.
functional value problem,existence,Caratheodory conditions,resonance
O175.8
A
1008-5513(2013)03-0255-09
10.3969/j.issn.1008-5513.2013.03.006
2012-11-16.
甘肃省自然科学基金(1107RJZA233);甘肃政法学院科研资助青年项目(GZF2013XQNW).
杜睿娟(1981-),硕士,讲师,研究方向:非线性常微分方程边值问题.
2010 MSC:34B15
