关于理想变压器的教学研究

郭继文

(西安铁路职业技术学院 机电工程系，陕西 西安710014)

“电路分析”课程中，理想变压器历来是教学中的重点和难点。对这一部分的教学内容有必要进行深入的研究和探讨，使学生能够深刻理解理想变压器作为电路元件模型的主要特性，并掌握相关的分析计算。

1 关于理想变压器的定义

大部分教材中对理想变压器都有一个叙述式的定义［1］:理想变压器是实际变压器的理想化模型。是对实际变压器的科学抽象，可以看作是极限情况下的耦合电感元件，其电路符号仍采用耦合电感元件的符号(图1)。理想变压器的三个理想化条件是:①变压器无损耗，即认为线圈的导线无电阻(通常叫做无铜损)，芯子的铁磁材料的磁导率为无限大(通常叫做无铁损);②耦合电感元件的耦合系数k=1，即全耦合;③参数无限大，即L1→∞，L2→∞，M→∞，但是满足

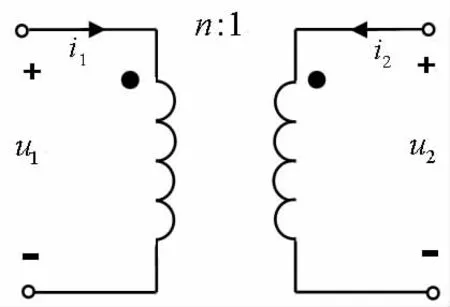
图1 理想变压器的电路符号

教材［2］利用伏安特性(即VCR)定义理想变压器，即将理想变压器视作一个理想电路元件加以定义:理想变压器是一种二端口元件，其电路符号仍与图1相同。理想变压器的VCR 为

式中，n 称为理想变压器的变比，是理想变压器的唯一参数。

采用前一种定义方式进行教学，比较符合学生的思维惯性，符合从个别到一般，从具体到抽象，从感性到理性这一认识上飞跃的规律，并且和学生在中学物理和大学物理课中的已有知识相衔接。而且学生对理想变压器相关知识的掌握比较具体，如初级线圈、次级线圈和同名端等。但在学生的头脑中建立的理想变压器是依赖于电磁感应工作的电路元件这一似是而非的认知。这里，理想变压器是被集中描述为变换交变电压及交变电流的理想化的电路元件模型［3］。

采用教材［2］的定义方式进行教学，是从一般到个别、从抽象到具体及从理论到实践，同样也是一种认识的飞跃。这种教学方法比较抽象，对学生而言，理解起来有一定的难度，但可以立即触及理想变压器这一元件的本质。理想变压器本质上是一种线性二端口电阻元件，尽管它采用耦合电感元件的电路符号，因为它的唯一参数只是变比n，而不是电感L1、L2和互感M 等。就理想变压器的定义式(即VCR)而言，它并非一种依靠电磁感应工作的电路元件，理想变压器的定义式对电压、电流的频率和波形没有任何限制，直流也是适用的。利用电磁感应来近似描述理想变压器概念仅适用于时变的电压和电流。这时的理想变压器可以看成是满足一定理想化条件的耦合电感元件，但它又和耦合电感元件有本质的区别。当耦合电感元件的电感L1、L2和互感M等参数由小变大，以至于大到无穷时，量变引起质变［4］。理想变压器和耦合电感元件就有了本质的不同，这是对学生进行辩证法教育的最好事例。

2 关于理想变压器的特性方程

关于理想变压器特性方程的具体推导，文献［5］给出了详细讨论，基本涵盖了大多数教材的推导方法。但在教学中还是有需要注意的一些问题。

在理想变压器的特性方程中，u1= nu2和i1=－(1/n)i2所满足的理想化条件并不相同，二者是各自在不同条件下获得的独立关系式，二者不是联列关系［6］。在无损耗的情况下，由耦合电感元件端口电压—电流特性方程，得

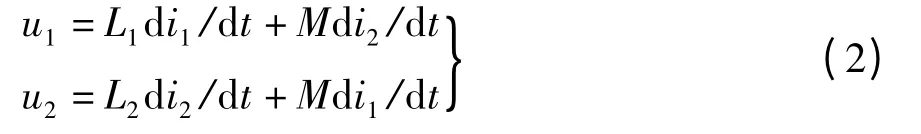
另一方面，如果设初级线圈和次级线圈的匝数分别为N1和N2，全耦合k =1 时的耦合磁通为Φ，则有

两式相比，有u1/u2=N1/N2。于是，u1/u2=N1/由此还可以得到变比n 的意义为n=N1/N2。这一部分内容在教学中一般不会引起异议。但是在推导i1=-(1/n)i2会出现问题。

由耦合电感元件端口电压—电流特性方程的第一式:u1=L1di1/dt+Mdi2/dt 可得

文献［4］和［6］采用两边取不定积分的办法，得

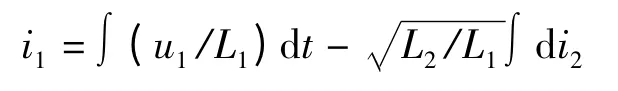
这时，加上第三个理想化条件，即参数L1和L2同比趋于无穷大，且有可得i1/i2但文献［4］在得到这一结论时提及了积分常数，指出略去两线圈中的任何直流电流分量，仅对时变电流部分而言得此结果。文献［6］并没有提及积分常数，直接得到结果这是教学中应该注意的一个问题。

文献［5］采用的是两边取定积分，即

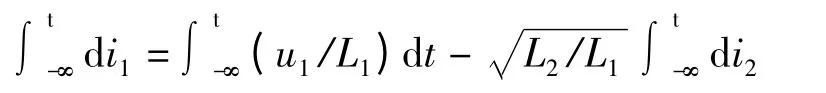
并给出条件i1(-∞)=i2(-∞)=0，便可得到结论这样，可避免积分常数的问题。

实际上，在这里也可以从实际的铁芯变压器出发，加上理想化条件，根据安培环路定律推导电流变换关系［5］，但这需要学生具有相应的知识储备。

特性方程中正负号与同名端位置的关系应该让学生掌握。事实上，在列写理想变压器特性方程时，当选取u1和u2的参考方向对同名端一致时，其电压关系式为u1=nu2。当选取i1和i2的参考方向对同名端一致时，电流关系式为i1=-(1/n)i2。

3 理想变压器的功率和能量

计算理想变压器的两个端口在任意时刻吸收的瞬时功率，绝大多数教材都是将理想变压器VCR 的两个方程相乘得到

由此得出结论，在任意时刻理想变压器吸收的瞬时功率为零，所以有功功率和无功功率均为零，理想变压器既不消耗能量，也不储存能量。只是从初级线圈输入的能量全部都能从次级线圈传输给负载。理想变压器是一个非动态、无损耗和无记忆的耦合元件。但如果我们如此教学，无法解释其中的物理机理。学生会产生疑问，耦合电感元件有储能，理想变压器却没有储能，为什么根据耦合电感元件抽象出来的理想变压器会和耦合电感元件具有如此根本不同的性质。

事实上，我们可以首先利用耦合电感元件的VCR 计算出耦合电感元件储存的能量。

在电压和电流取关联参考方向下，耦合电感元件吸收的功率为

由于在t=-∞时，i1(-∞)=i2(-∞)=0，耦合电感元件无储能。因此，从－∞到t 这段时间内，耦合电感元件储存的能量为

从上式可以看出，耦合电感元件的储能并不为零。但考虑到理想变压器的理想化条件，即k =1，或者，则有

再利用理想变压器的特性方程:i1/i2=-1/n=代入上式，很容易得到

显然，如果改变同名端的位置，也能得到同样的结论。这说明，只要满足理想变压器的定义条件，在任意时刻，理想变压器的储能就恒等于零。这和大多数教材只是指出瞬时功率恒等于零相比更能说明理想变压器既不消耗能量，也不储存能量的本质。

这里需要强调两点。第一点，从上面的推导过程可以看出，必须满足理想变压器的全部理想化条件，才能得出储能恒等于零这一结论。这也就说明了同样作为实际变压器电路模型的空心变压器和全耦合变压器不能得到这一结论的原因。另一方面，空心变压器和全耦合变压器均需要一定的励磁电流维持其磁通［7］，所以无功功率一定不为零。而理想变压器不需要励磁电流，其无功功率就为零，这也从另一个角度说明了理想变压器是不依赖于磁场工作的。第二点，理想变压器既不消耗能量，也不储存能量的性质是对端口外而言的，在其内部，是存在着能量的传输和流动。

4 结语

理想变压器是“电路分析”课程的经典内容，属于传统的教学内容，其定义也是给出耦合电感元件之后引出的。但是，关于理想变压器的教学理念和教学方法仍值得深入探索和研究。就实际变压器的电路模型而言，有空心变压器、全耦合变压器和理想变压器之分。它们既有联系，又有区别，尤其是理想变压器和空心变压器、全耦合变压器有着本质的区别。在教学中充分注意到这一点，就能取得更好的教学效果。

［1］ ［美］Charles K.Alexander，Matthew N.O.Sadiku.电路基础［M］(第3 版)关欣等译.北京:人民邮电出版社，2009年9月

［2］ 陈洪亮，张峰，田社平.电路基础［M］.北京:高等教育出版社，2007年5月

［3］ 陈崇源.高等电路［M］.武汉:武汉大学出版社，2000年3月

［4］ 李瀚荪.简明电路分析基础［M］.北京:高等教育出版社，2002年7月

［5］ 陈希有，刘风春，董维杰，李冠林.理想变压器特性方程教学方法讨论［J］. 南京:电气电子教学学报. 2010年 第32 卷 第4期55-58

［6］ 邱关源.电路［M］(第五版). 北京:高等教育出版社，2006年5月

［7］ 田化梅，钱菁.电路分析［M］武汉:湖北科学技术出版社，2004年10月