雷达目标高度公式推导及适用性研究

徐振海，饶 彬，赵 锋，王 伟

(国防科技大学 电子科学与工程学院，湖南 长沙410073)

0 引言

在“雷达原理”课程教学中，讲完目标距离测量和角度测量以后，目标高度可以由目标距离和仰角导出，目标测高通常一带而过。雷达原理相关教材［1，2］以及《雷达手册》［3］中都不加推导地给出测高公式。针对三坐标监视雷达典型探测场景，目标仰角通常小于30o，对于近距离目标的目标高度为

对于远距离目标的目标高度为

式中，r 表示目标距离;θ 表示目标仰角;地球等效半径Re=8500Km，这里等效地球半径为实际地球半径的4/3 倍。在课堂讲授过程中，式(1)非常容易理解，但式(2)理解起来较困难。这个公式的由来教材中没有提及。究竟何为近距离目标?何为远距离目标?测高精度如何?学生对这些知识点提出了较多疑问。笔者鉴此，对该问题进行了较深入研究。

1 目标高度公式的推导

对于近远距离目标，地球表面不能看作平面，电波传播也不能看作直线。对于电波的弯曲问题可以用等效地球半径的方法来解决。对于远距离目标可以看作直线传播。此时雷达和目标的几何关系如图1所示。

在图中的ΔAOT 中，利用余弦定理不难得出

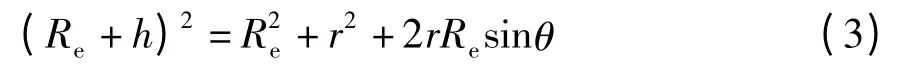
因此，在已知目标距离和仰角的条件下，目标高度可精确求出:

由于该公式较繁琐，我们可以在降低精度的条件下寻求更简洁的解法。

图1 考虑地球曲率时雷达—目标几何关系

将上式进一步变形为

其中，X= (r2+2rResinθ)/R2e= r2/R2e+2rResinθ/Re。通常情况因rRe，所以X1，利用泰勒公式可得

将上式代入式(5)，并忽略掉一阶以后的所有项，近似得到

由此，便得到了式(2)。可见测高公式是精确公式泰勒展开后的一阶近似结果。可以设想，如果保留二阶项采用二阶近似，则测高精度将进一步提高。所以要在精度和计算复杂度之间折衷考虑。

由上式可以看出，一阶项以后所有项均为截断误差，但二阶项是误差的主体部分。根据相对误差的定义，一阶近似所造成的测高公式相对误差为

可见相对误差与目标的距离和仰角都有关系，目标距离越近、仰角越低，该公式的精度越高。在应用测高公式(2)时，一定要明白该公式也是有误差的，当误差超过容忍范围时，公式不再适用。

2 适用范围分析

如果要求截断造成的相对误差必须小于某水平α0，或者说误差容忍水平为α0，即 X/4 =α0或 X≤4α0。于是进一步可得

求解一元二次不等式可得

满足上述不等式的区域就是测高公式的适用范围，等式表示适用范围的边界。

适用区域的边界如图2曲线所示，曲线下方的区域表示公式适用的范围。可以看出:如果相对误差容许水平为1%，即当目标高度1km 时，公式误差为10m。因此在正常的雷达探测范围内，该公式都是适用的。如果相对误差容许水平为0.1%，即当目标高度1km 时，公式误差为1m，公式适用范围将大大减小了。如果目标仰角10o，目标最大距离100km;如果目标仰角4o，目标最大距离200km。

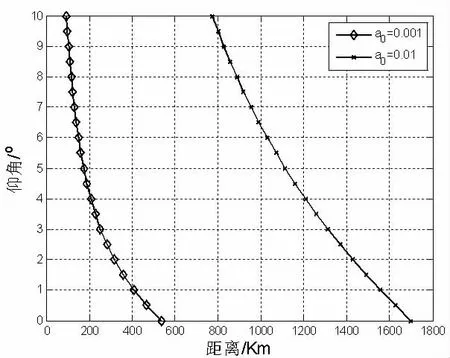
图2 容忍误差条件下公式适用范围

3 结语

本文详细推导了目标测高公式，并进一步分析了公式适用性问题。该研究的意义有两个方面:在“雷达原理”的教学方面，该研究对雷达原理教材是有益的补充，对“雷达原理”知识点的讲解以及学生的理解都十分有利;在雷达工程实践方面，该研究提醒工程师使用雷达手册中目标测高时，公式也是有误差的，在测高精度要求很高的场合，该公式有特定的适用范围。

［1］ 丁鹭飞，耿富录，陈建春，雷达原理(第四版)［M］，北京:电子工业出版社，2011.05，361-362

［2］ 王雪松，李盾，王伟，等，雷达技术与系统［M］，北京:电子工业出版社，2009.08，130-131

［3］ 斯科尔尼克，雷达手册(第二版)，北京:电子工业出版社，2003.07，796-797