制定综合评价指标时各主成分权重系数确定方法研究

马建华

（淮北师范大学 数学科学学院，安徽 淮北 235000）

为科学有效地评价某种现象或结果，需要有一个科学的评价指标.为此，人们通常用主成分分析方法，先对原变量进行主成分分析，从中提取若干个主成分，然后给各主成分以一定的权重系数，把这些主成分相加构成一个综合评价指标，以此对要评价的对象进行计算，根据计算结果对评价对象作评价.这里有个关键问题：各主成分的权重系数如何确定.这个问题直接影响到评价结果科学性和有效性.笔者经过分析比较和科学论证，给出一种称为“主客观结合法”的确定方法.即，如果用T表示综合评价指标，则有

其中Yi是第i个主成分，λi是第i个主成分的特征值（方差），ai是第i个主成分的主观系数.

下面讨论该方法的科学性，为此先考查目前已有的3种确定方法：直接相加法、特征值法及主观系数法的科学性.

1 对目前已有两种确定方法的讨论

1.1 直接相加法

该方法是把主成分分析得到的若干个主成分直接相加得到综合评价指标.即，其中Yi是第i个主成分.

该综合指标各主成分系数均为1，根据方差意义可知，其第j个主成分对评价结果的贡献率（影响程度）是，其中λj是第j个主成分的特征值（方差），这种影响程度未必合理，未必符合研究目标.

比如，在一个研究建立大学生综合素质评价指标的问题中，用主成分分析法，从9个原变量中提取4个主成分，如表1，表2所示.

观察表2可知，第一主成分，主要反映的是大学生思想品德方面的内容；第二主成分，主要反映的是大学生文化课学习成绩方面的内容；第三主成分，主要反映的是大学生英语水平；第四主成分，主要反映的是大学生体育方面的内容.各主成分的方差依次为：4.387，1.580，1.244和1.012 .按公式计算得各主成分的贡献率依次为：53.35%，19.21%，15.13%，12.31%.由此可看出，反映大学生思想品德的第一主成分，贡献率超过一半，而反应大学生文化课学习成绩的第二主成分，却只有19.21%，显然这是不合理的.

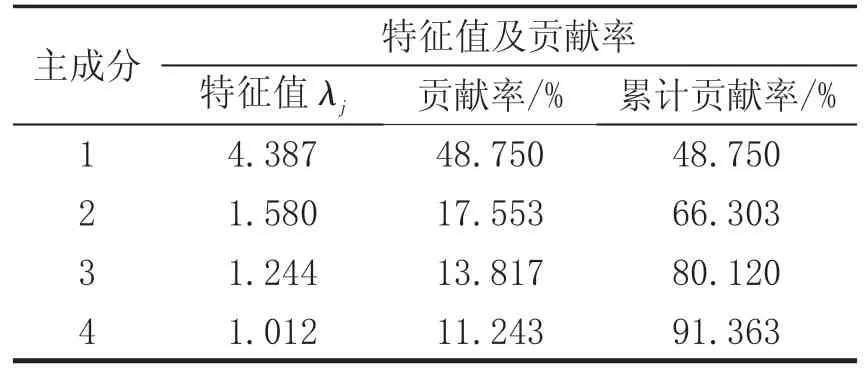
表1 旋转后的特征值及贡献率

表2 旋转后的主成分矩阵

1.2 特征值法

该法是以各主成分的特征值的算术根（各主成分的标准差）为权重系数构造综合指标.

该综合指标第j个主成分的系数为，由方差的性质得：

因此第j个主成分对评价结果的贡献率（影响程度）是，这种影响程度是：大者更大，小者更小，这在许多情况下是很不合理的.

1.3 主观系数法

该方法是在对原变量进行主成分分析，提取出必要的主成分后，根据各个主成分的意义（即该主成分是反映评价事物的哪个方面的内容），按照评价目的，由有关专家、领导或相关人士，根据各主成分在该评价中的重要性给出各主成分的权重系数ai，称之为主观系数.此方法构造的综合指标为：，其中Yi是第i个主成分，ai是第i个主成分的主观系数.

该法似乎能科学合理地实现评价目标.但是忽视一个重要问题：各主成分方差的差异对实现评价目标的影响.

下面还是用表1，表2的数据来说明.根据4个主成分的意义及评价目的，如果以2，6，1，1为第一，第二，第三及第四主成分的主观系数，那么按公式，计算得第一，第二，第三及第四主成分的贡献率依次为：22.88%，74.18%，1.62%和1.32% .由此看来，这与评价的预期有一定差距，尤其是后两个主成分的贡献率与预期的10%相差太多.

通过上面对已有的3种方法进行的讨论，我们知道它们都存在一定的问题.为解决这些问题，笔者提出一种新的确定方法—主客观结合法.

2 主客观结合法的讨论

该方法是在对原变量进行主成分分析，提取出必要的主成分后.根据各个主成分的意义，按照评价目的，由有关专家、领导或相关人士，根据各主成分在该评价中的重要性给出各个主成分的主观系数：ai，然后考虑到由于各主成分自身方差()λi不同，其对综合评价指标的影响程度不同，用作为第i个主成分的权重系数建立综合评价指标.

根据方差性质得

由此，根据贡献率的意义可得到，第j个主成分对评价结果的贡献率（影响程度）是，这样的贡献率才是我们预期的.

仍以表1，表2的数据来说明.根据4个主成分的意义及评价目的，如果以2，6，1，1为第一，第二，第三及第四主成分的主观系数，即：a1=2,a2=6,a3=1,a4=1；那么按公式计算得四个主成分对评价结果的贡献率分别为：20%，60%，10%和10%，这样的贡献率正是我们所预期的.

通过以上分析讨论可知，按主客观结合法确定的系数更加科学有效，更能满足评价目的需要.

3 主客观结合法的具体实现

由于在做主成分分析时，一般都是对相关矩阵进行的，得到的主成分是标准化原变量的线性组合，不便于应用.因此，在使用前有必要将评价指标转变为原变量的线性组合.即

下面对参考文献［1］中83名同学用该综合指标进行评价并排名.为此，先把综合指标中的变量转换为原变量：政治品质（X1）、学习态度（X2）、法纪观念（X3）、集体观念（X4）、社会公德（X5）（这5个指标是由学校每年一次的综合测评时，学生互相打分的结果.综合测评时，要求每位同学必须给全班同学的各项对照相应标准打分，每项20分）、英语水平（X6）（各次英语考试成绩的平均）、体育（X7）（各次体育测试成绩的平均）、专业课成绩（X8）（各门专业课成绩的平均）、公共课成绩（X9）（除英语，体育课以外的所有公共课成绩的平均）.

根据四个主成分的意义及评价目的，以2，6，1，1 为第一，二，三，四主成分的主观系数，即：a1=2,a2=6,a3=1,a4=1，由表1知，λ1=4.387，λ2=1.580，λ3=1.244，λ4=1.012，因此得到以下综合评价指标：

其中，bij是第i个主成分中第j个标准化变量的系数（见表2）.

表3 变量标准差

按公式（※）计算得综合评价指标如下：

按照此公式容易算得该班83名同学2009－2010学年综合排名，此排名可作为奖学金或评优的重要依据.

表4 全班83名同学2009－2010学年综合排名

［1］马建华.高师院校学生综合素质评价指标的科学确定［J］.数学的实践与认识，2012（10）：1-5.

［2］范金城，梅长林.数据分析［M］.北京：科学出版社，2002.

［3］茆诗松，程依明，濮晓龙.概率论与数理统计教程［M］.北京：高等教育出版社，2004.