一种阈值化的小波图像去噪算法

薛明志，李天钧

(1.商丘师范学院 数学与信息科学学院，河南 商丘 476000;2.郑州大学 软件学院，河南 郑州 450001 )

0 引 言

图像处理过程涉及数字图像的采集、传输等环节，每一个环节都可能出现图像的噪声.而这噪声会对图像的处理环节，如分割、增强、检索等产生直接影响.因此，许多学者讨论了图像去噪算法.

使用小波变换是进行图像去噪的一种有效方法，原因在于小波变换具有多分辨率、快速算法等特点.据我们所知，小波系数相关性原理、小波变换模极大值原理和小波系数阈值化函数是三种常用的去噪方法.关于小波基本理论、变换和小波在图像的应用，见文献［1］.特别指出的是，Donoho 于1995年针对图像去噪提出了小波阈值萎缩法［2］.该方法比较好，它根据图像噪声及信号在小波变换后的幅度分布进行相应展开.尽管如此，可也会出现伪吉布斯现象等视觉失真的缺点;而软阈值方法会造成高频信息丢失、边缘模糊等失真.因此，很多学者都针对性地提出了一些解决方案和改进方法，如多项式插值法、软硬阈值折衷法、模平方处理法、最大似然估计法、半软阈值法和修正软阈值法等［3－5］.鉴于上述分析，本文给出新的阈值化函数，以达到提高信噪比、改善去噪效果.最后进行了仿真试验，实验表明，我们构造的函数可以改善硬、软阈值化方法中存在的边界模糊和振荡，也显示出在阈值化处理过程中具有自适应性.

1 Mallat的去噪原理

Mallat的结果［6］为

定理1 设0≤n≤1，函数f(x)定义在［a，b］上.那么f(x)满足一致的Lipschitz 指数n 当且仅当存在常数k ＞0，使∀x ∈［a，b］有

在(1)式两边取对数得

在小波变换后域中，有效信号的性态表现与随机噪声的表现有所不同，因此当尺度变化时，两者的小波系数幅度变化出现相反的态势.这样，如果变换尺度较大，那么可认为信号完全主导了小波系数;如果变换尺度较小，那么可认为噪声几乎完全控制了小波系数.正是这个特性才是我们有理由说明，小波变换后可以辨别噪声与信号.但在应用中，使用小波对图像去噪往往是先设定阈值，然后分离信号和噪声.这种方法的依据就是某分解尺度下具有不同的噪声小波系数幅度与信号小波系数幅度.

2 改进的阈值算法

2.1 Donoho 阈值算法

D.L.Dohono 提出的阈值化方法(［2］)可以分为硬阈值法与软阈值法.

硬阈值化方法规则为

软阈值化方法规则为

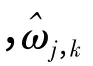
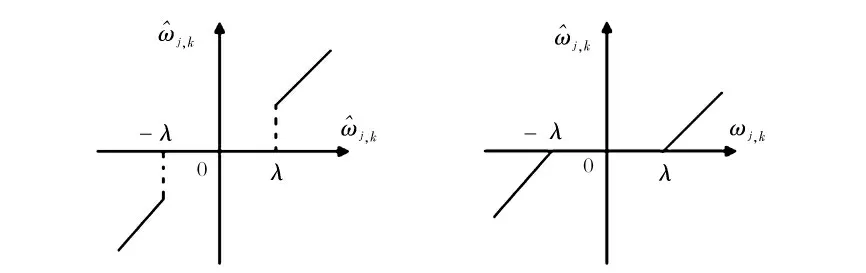
图1 硬阈值化(左)和软阈值化(右)方法Fig.1 The method of hard threshold (left)and soft threshold (right)

2.2 阈值算法的改进

本文结合软、硬阈值化函数的不同特点，构造了一种新的阈值函数:

其中α 与β 为调节参量，α ≥0，0≤β≤1.

以下对函数连续可导性进行考察:

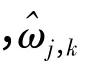
此外，阶次的调节是可由α的不同选择而实现:α=0 且β=1 是软阈值化;α=0 且β=0 是硬阈值化，此时阈值函数为原信号函数;α→+∞且0≤β≤1，也是硬阈值化函数.因此，给出的新函数就是介于硬、软阈值化之间的可调整函数.在具体应用中，为达到最佳效果，我们可调整参量α 和β 来处理不同的图像.

2.3 仿真实验

我们取用双正交小波函数bior6.8，同时选4 层分解层.将这里改进的阈值、软阈值和硬阈值分别作用于含有随机噪声的sinsin 图像来实验图像去噪.在实验中，α 取3，β 取0.5，并且每层上的经验系数取Birge－Massart 策略中的经验系数.下图为仿真效果图.

图2 不同阈值化方法作用后的效果图Fig.2 The effective image processed by different threshold methods

以下通过均方误差MSE 和峰值信噪比PSNR 两项指标对去噪效果进行统计计算.对于一幅像素为N×M的图像，定义均方误差MSE 为

定义峰值信噪比为

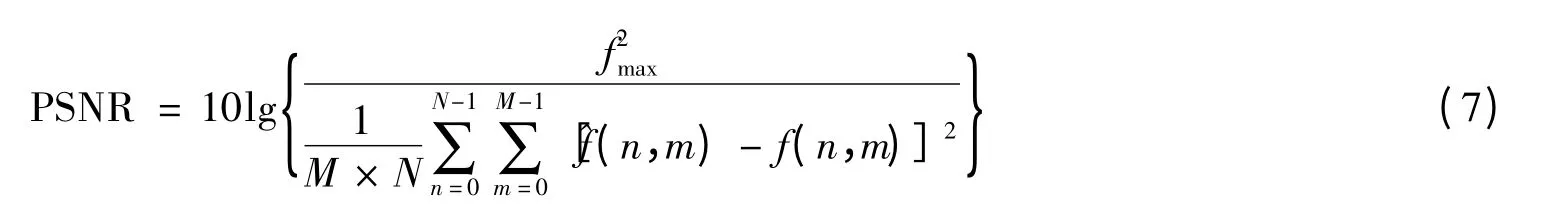
其中fmax=maxf(n，m);n=0，1，…，N－1;m=0，1，…，M－1;f(n，m 和^f(n，m)分别为图像在(n，m)位置上的像素的灰度值和经去噪后的灰度值.

实际应用中，由于图像各种各样及它们包含的噪声也不尽相同，所以最终会采用不同的参数.下表给出了实验数据统计结果.

表1 图像阈值化去噪后的MSE 和PSNR 统计Table 1 Statistics of MSE and PSNR processed by image threshold de－noising

3 结 语

本文首先对Dohono的硬、软阈值化方法存在的问题进行了分析;其次，针对存在问题，构造了新的阈值化函数，该函数通过调整参量α 和β的取值可达到较优的小波系数阈值估计.最后进行了仿真试验，试验结果表明，新方法可较好地去掉图像中噪声，并且有效地弥补了Dohono的硬、软阈值化方法中存在的一些不足，如边缘模糊、高频信息“过扼杀”等，以及伪吉布斯效应、振荡等视觉失真.

［1］李登峰，杨晓慧.小波基本理论与应用实例［M］.北京:高等教育出版社，2010.

［2］Donoho David L.De－noising by soft－thresholding［J］.IEEE Trans on Information Theory，1995，41(3):613－627.

［3］付炜，等.一种改进的小波域去噪算法［J］.计算机工程与应用，2006，42(11):80－81.

［4］刘卫东，等.小波阈值去噪函数的改进方法分析［J］.高电压技术，2007，33(10):59－63.

［5］张弦，等.一种改进的小波阈值去噪方法［J］.微计算机信息，2007，23(11－1):309－311.

［6］Mallat S.Singularity detection and processing with wavelets［J］.IEEE Trans on Information Theory，1992，38(2):617－643.