基于卡尔曼滤波算法的弹箭飞行姿态测试方法

2013-07-03王勇贞

山西电子技术 2013年2期

王勇贞

(中北大学电子测试技术国家重点实验室，山西太原 030051)

0 引言

获取弹箭的飞行姿态信息对分析其飞行动力学特性具有重要意义。在现代武器试验中，常用遥测系统获取各系统的工作状态参数，为评定导弹的性能及为进行导弹故障分析提供依据。目前国内外对于弹体飞行姿态参数，常用的捷联惯导系统是采用加速度计法进行测量，但由于传统的加速度计存在安装复杂、安装精度要求高、解算复杂等问题，文中舍弃了加速度计作为惯性器件，而是选用MEMS 陀螺作为惯性器件。MEMS 陀螺是根据牛顿惯性定律的原理进行测量的，此方法受外界因素影响较小，在过载不太大时应用较方便，但是MEMS 陀螺误差随时间积累［1，2］。文中将地磁传感器引入惯性测量系统进行组合设计，抑制系统输出误差，并在此基础上设计了卡尔曼滤波器进行信息融合用来修正捷联惯导系统的累积误差。

1 基于地磁/MEMS 陀螺的卡尔曼滤波算法

基于地磁/MEMS 陀螺组合测量弹箭飞行姿态的多传感信息融合算法，采用这种组合可以提供两种具有高度互补特性的独立信息源，MEMS 陀螺提供时间长、稳定性高的数据，地磁传感器提供时间短、精度高的数据，最终通过Kalman 信息融合算法将这两种数据处理并获取相对准确的弹箭飞行姿态信息。卡尔曼滤波算法［3］是一个高效的最优化自回归数据处理算法，它实质上是通过系统的量测值重新构造系统的状态向量，并以“预测—实测—修正”的模式顺序递推，它利用测量系统的系统噪声和量测噪声的统计特性，把系统的观测量作为滤波器的输入，把所要求取的参数估计值作为滤波器的输出，通过空间状态更新和观测更新算法有效地组织在一起，最后根据系统的状态方程和观测方程计算出我们所需要的参数。

使用三轴陀螺角速度传感器测量姿态角的方法很多，比如有:四元数法、欧拉角法、卡尔丹角法、等效旋转矢量法等［4］。由于四元数法的计算量相对比较小、算法简单，因此在基于地磁/MEMS 陀螺组合测量系统中采用四元数姿态更新算法。基于地磁/MEMS 陀螺的卡尔曼滤波算法如下所述，当弹箭飞行体的初始位置确定(即弹箭飞行体的初始姿态角已知)以后，可推导求出四元数的初始值，四元数的初值计算公式如下:

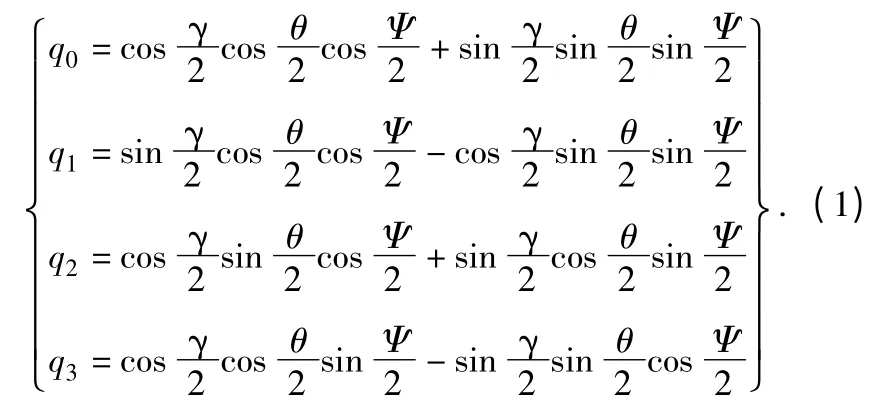
根据MEMS 陀螺的三轴输出数据求出采样时间间隔的角增量，依据四元数微分方程的毕卡求解法就可以求出各个时刻的四元数，但是由于MEMS 陀螺存在累积误差，因此上面求出的四元数存在一定的误差，需要利用地磁传感器的输出信息对它做出修正，该修正过程是通过卡尔曼滤波算法将陀螺数据求出的四元数与地磁传感器的输出信息进行信息融合求出最优的四元数，最后经最优的四元数计算出弹箭飞行体的飞行姿态角信息。在卡尔曼滤波算法中采用毕卡求解法的四阶近似算法作为滤波系统的状态方程，如下所示:

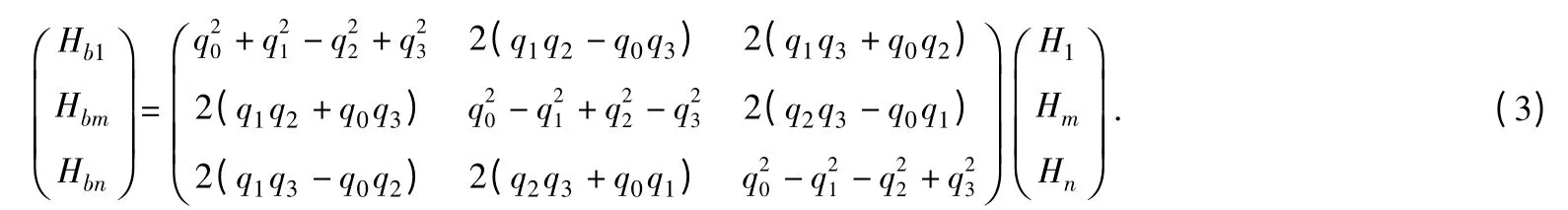
式中，Hb1、Hbm、Hbn为系统的观测量。假设系统的噪声驱动矩阵Γk，k－1为单位矩阵，{Wk}和{Vk}是互不相关的零均值白噪声序列。

2 软件仿真条件

下面对所建立的基于地磁/MEMS 陀螺的卡尔曼滤波算法进行软件的仿真和算法分析，仿真软件采用MATLAB 软件。实验中的地磁信息采用太原地区的地磁参数，如下式所示:

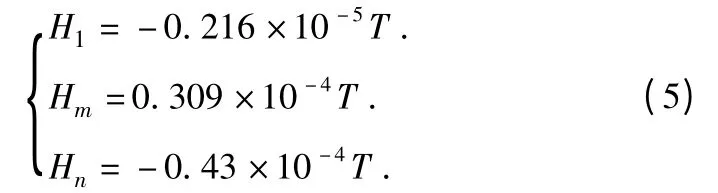
由于该课题主要用来解决近程高自旋的小型弹箭的飞行姿态测试，所以假设弹箭的姿态角变化规律如下式所示:

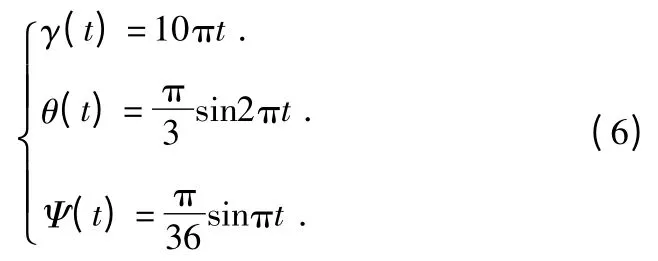
式中，t为时间，采样频率为10k/s ，采样总时间为10s 。有了式(6)所假设的运动规律我们可求出陀螺三个轴的输出，求解公式如下:

现在，根据前面所构造的卡尔曼滤波算法模型即可进行编程和软件仿真。

3 软件仿真结果与分析

在仿真条件下，采用卡尔曼滤波信息融合算法对基于地磁/MEMS 陀螺组合测量弹箭飞行姿态的仿真结果如图1所示:

图1 弹箭飞行姿态角仿真结果曲线

仿真条件下，弹箭飞行姿态角误差曲线如图2、图3和图4所示:

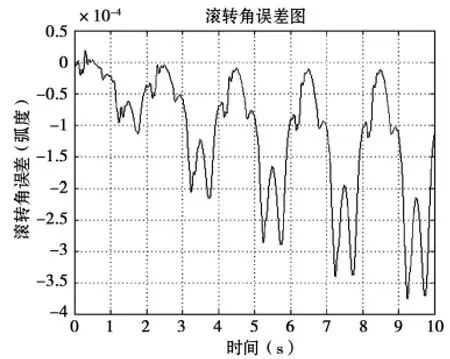
图2 滚转角误差曲线图

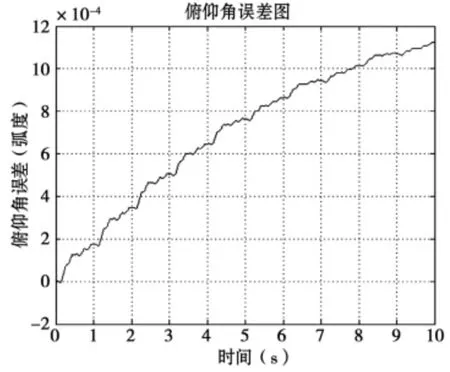
图3 俯仰角误差曲线图

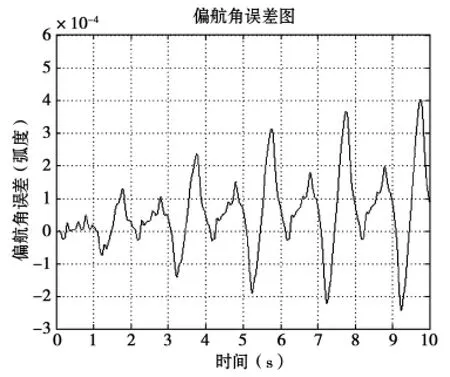
图4 偏航角误差曲线图

从仿真结果图2 到图4所示，滚转角误差在仿真时间内最大幅值为3.8×10－4弧度，俯仰角误差在仿真时间内的最大幅值为11.3×10－4弧度，偏航角误差在仿真时间内的最大幅值为4×10－4弧度，这些误差随着时间的推移整体上有放大的趋势，通过分析可知这些误差主要来自模型的不准确，而误差随时间的推移有放大趋势则可能是由于算法的递推特性引起的，同样模型不准确也可能引起误差随时间的推移而放大，但从仿真结果看它也足以满足小型弹箭的飞行姿态测试要求了，从这些仿真图的结果看，基于地磁/MEMS 陀螺的卡尔曼滤波算法理论上是完全可以满足对小型弹箭飞行姿态测试技术要求的。

另外通过大量的实验发现如果飞行体的各个姿态角变化频率和幅度越大该算法受误差的影响越小。因此该算法比较适用于高动态短近程的小型弹箭的姿态测量。