车间调度问题的量子粒子群优化算法设计
2013-07-03肖蕾蕾史二娜
肖蕾蕾,史二娜
(西安科技商贸职业学院,陕西 西安 210096)
0 引言
为了提高PSO算法中粒子的随机性和PSO算法的全局搜索性能,sun 于2004 年提出了量子粒子群优化算法(Quantum- behaved Particle Swarm Optimization,QPSO)[1,2],以DELTA 势阱为基础,从量子力学的角度出发,赋予粒子量子行为,使其在量子空间中搜索。在量子空间中,由于量子状态的叠加、相干和纠缠特性,粒子可能出现在搜索空间的任何位置。而在PSO算法中,绝大多数粒子的搜索空间被限制在搜索空间的某个范围内,可能存在搜索“禁”区[1],因而QPSO算法的全局搜索性能远远优于PSO算法,并且QPSO的全局收敛性已经得到了证明[3]。
1 量子粒子群算法
1.1 量子粒子群优化算法数学描述
QPSO算法通过波函数ψ(x,t)来描述粒子的状态,并通过求解薛定愕方程得到粒子在空间某一点出现的概率密度函数,再通过Monte Carlo 随机模拟得到粒子的位置方程为:
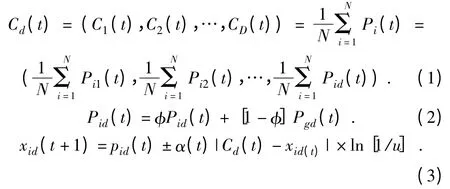
式中:N—种群中粒子数目;D—粒子的维数;u和φ—在[0,1]区间上均匀分布的随机数;Pid(t)—局部吸引点;Cd(t)—种群中所有粒子的平均最好位置点。和标准PSO算法一样,Pi和Pg为粒子i所经历的最好位置和种群中所有粒子所经历的最好位置;α(t)为收缩扩张系数,是QPSO算法的唯一的控制参数。
1.2 基于量子粒子群算法的粒子编码方式
编码问题是设计算法的首要的关键问题。粒子编码方式仍采用基于工序的编码方法,对于n个工件m 台机床的Job-shop 调度问题,分别用自然数1,2,…,n 表示每个不同的工件,由于每个工件有m 道工序,这样就总共有n×m 道工序。采用基于工序的表达方法进行编码[4],即用一个长度为n×m的粒子代表一种排序方案,粒子中的每一个元素对应的是工件标号,然后根据工件标号在序列中出现的顺序确定该工件的工序。
1.3 基于量子粒子群算法目标函数及适应值的计算
结合各工件的工艺约束和各工序完成时间约束,仍将各个粒子的最大完成时间作为适应度值,最大完成时间的具体计算过程如下[4,5]:
(1)将所有工件所对应的第一道工序的开始加工时间初始化为零。
(2)为每台机器设定一个加工链表,用于表示该机器上加工的工件及顺序。
(3)执行调度方案中的第一个加工操作,将该操作加入到所对应的加工机器的加工链表中,记录该工件第一道工序的开始加工时间和加工结束时间,并将该工件下一道工序的理论开始加工时间设置为该工件第一道工序的加工结束时间。
(4)顺序执行调度方案中的其他加工操作,将这些加工操作依次加入到该操作所对应的加工机器的加工链表中。
(5)执行完毕调度方案中的所有加工操作后,比较所有工件最后一道工序的加工结束时间,取最大值,即为当前调度方案的最大完工时间。记录所有机器的加工链表,即为当前调度方案的实际调度结果。
1.4 量子粒子群算法参数的选择
在QPSO算法中,除了群体大小、问题维数与迭代次数外的唯一控制参数为式(3-5)中的压缩-扩张因子α,它在算法中起到的作用是能够调节算法的收敛过程。尽管算法只有一个控制参数,但是尚未对其进行过系统的研究。在文献[8]中,通过仿真结果得知QPSO算法的压缩-扩张因子必须满足α <1.781 才能保证粒子的收敛,否则算法将肯定不能保证收敛。在这样的前提条件下,如何选择α的取值及取值方式已成为一个重要的研究课题。文献[3]提出了α的三种控制策略:固定取值策略,线性减小取值策略及非线性减小取值策略。结合标准测试函数的仿真结果得出:固定取值策略的鲁棒性较差;采用控制参数线性减小的取值方式并且线性减小的取值范围在[0.8,0.6]和[1.0,0.5]时能够对绝大多数的函数取得较好的优化结果;而非线性减小的取值策略也能够取得一些较好的结果。
本文采用α 线性减小的取值方式,计算公式如下:

式中,α1<α0,α0和α1分别是控制参数α的初始值和终止值。
1.5 量子粒子群算法位置的初始化
对于粒子的初始位置,本文将xid任意随机数,即:

式中rand()是随机产生的任意实数。
1.6 量子粒子群算法位置的更新
对于n个工件m 台机床的Job-shop 调度问题,位置矢量应该是一个n×m 维实向量,分别根据式(1)、(2)和式(3)进行平均最好位置点Cd(t)、局部吸引点pid(t)和位置矢量的更新。在位置迭代过程中,‘±’是由(0,1)之间产生的随机数决定的,当产生的随机数大于0.5 时取‘-’,其余取‘+’,并且表示粒子的二维向量的第一维向量保持不变,待粒子位置更新之后对粒子位置矢量进行从小到大的排序,进而生成待加工的工序序列,然后解码生成调度方案。
1.7 量子粒子群算法流程
Step1:初始化α0、α1、tmax,并且设当前进化代数t=0。
Step2:设定种群数N,随机初始化各粒子的位置矢量。
Step3:将各粒子位置矢量映射为工序序列,计算各个调度方案的最大完成时间,从而对各个调度方案的性能指标进行评价。
Step5:根据式(1)计算粒子的平均最优位置C(t)。
Step6:判断t是否等于tmax,如果t=tmax,则输出Pg(t),并由Pg(t)得到最优调度方案;否则,执行Step6。
Step7:对种群中所有粒子进行如下操作[6,7]:
①按式(4)更新压缩-扩张因子α(t),按式(2)更新粒子局部吸引点位置Pi(t),然后按式(3)更新粒子位置Xi(t),并将粒子位置矢量映射为新的工序序列。
②计算粒子的最大完成时间。
③若粒子的最大完成时间小于Pi(t)对应的最大完成时间,则Pi(t)=Xi(t);若粒子的最大完成时间小于Pg(t)对应的最大完成时间,Pg(t)=Xi(t)。
Step8:令t=t+1,转Step6。
2 典型算例仿真结果
2.1 FT06 问题的寻优结果
FT06(6×6)标准测试问题每个工件的加工路线与每道工序对应的加工时间见表1。

表1 FT06(6×6)问题工件工序与工时
FT06算例的第一行数据表示工件1 先在机器3 上加工1s,然后在机器l 上加工3s,然后在机器2 上加工6s,依次类推,最后在机器5 上加工6s。
2.2 FT06 问题的仿真结果
取种群数目N=20,最大迭代次数tmax=100,分别采用PSO算法和QPSO算法连续运行20 次所得到的结果如表2所示。
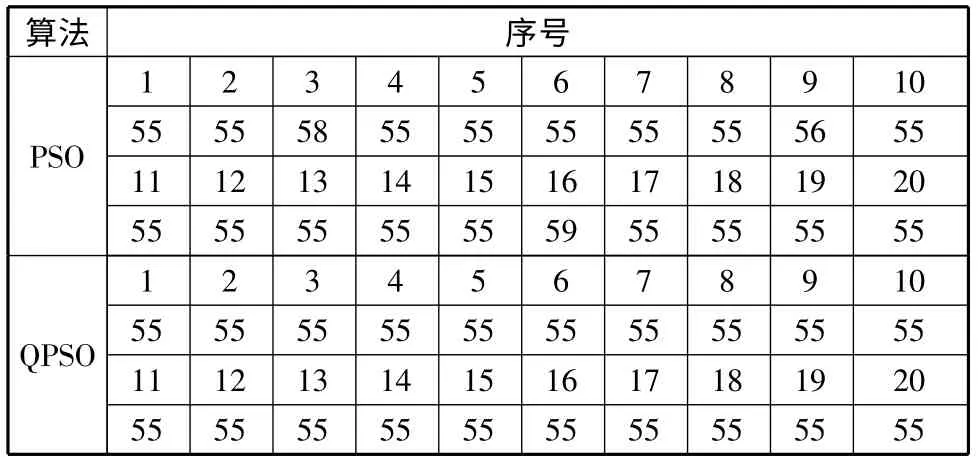
表2 基于PSO和QPSO算法的FT06 问题仿真结果
从表2 可以看出,采用PSO和QPSO算法找到的最优调度的最大完工时间为55s。而FT06Job-shop 调度问题在参考文献[4]中用基于位置矢量更新的粒子群算法调度后,最大完工时间为55s ,用基于遗传算法的粒子群算法调度后,最大完工时间也为55s,说明PSO和QPSO算法在求解FT06Job-shop 调度问题上取得了较好的效果。
考虑到优化算法的收敛效果也是评价该算法优化性能的重要指标,由于两种算法在求解FT06Job-shop 调度问题时都取得了较好的效果,这里就给出了两种算法求解FT06Job-shop 调度问题时的各代种群最优调度结果的收敛效果图。PSO和QPSO 每一代的最小值收敛效果如图1所示,PSO和QPSO 每一代的平均值收敛效果如图2所示。

图1 PSO和QPSO 每一代的最小值收敛效果
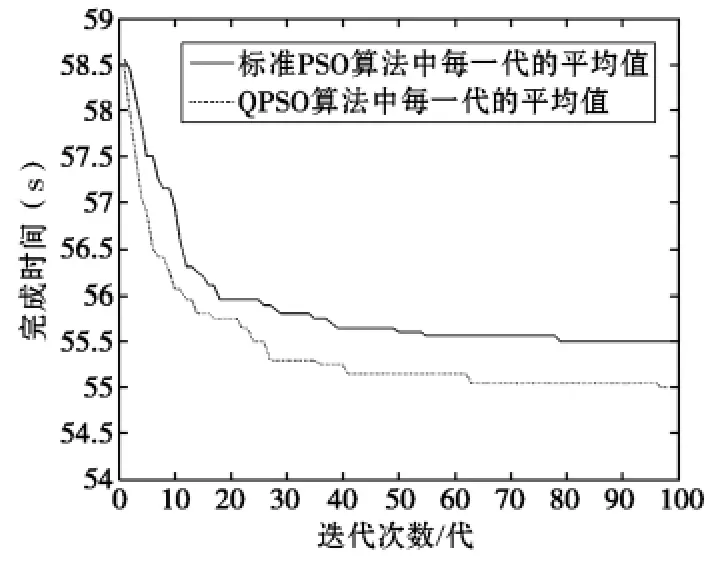
图2 PSO和QPSO 每一代的平均值收敛效果
由图1和图2 可以看出,对于FT06 车间调度问题,QPSO算法在求解FT06Job-shop 调度问题时的效果明显好于PSO算法。
2.3 仿真结果分析
由于在经典PSO算法中粒子的收敛是以轨道的形式实现的,并且由于粒子的速度总是有限的,因此在搜索过程中粒子的搜索空间是一个有限的区域,不能覆盖整个可行空间。QPSO算法,量子系统的粒子在测量之前没有既定的规程,而已一定的概率分布出现在任何位置,从而可以达到全局搜索。从动力学的角度看,QPSO算法中粒子的收敛过程是以局部吸引点p为吸引子,随着速度的减小不断地接近p点,最后跌落到p 点[9,10]。因此在整个过程中,在p 点处实际上存在某种形式的吸引势能场吸引着粒子。这正是整个粒子群能保持聚集性的原因。而且,QPSO算法的控制参数较PSO算法更少,因此QPSO算法相对于PSO算法而言,可以避免算法陷入局部极值从而具有更好的全局收敛性能。因此,在FT06算例仿真结果中,QPSO的寻优能力均优于PSO算法。
3 结论
本文通过典型车间调度问题算例验证了粒子群算法和量子粒子群算法解决车间调度问题的有效性及优越性,通过车间调度问题FT06算例的仿真结果证明QPSO算法的寻优能力优于PSO算法。
[1]Sun J,Feng B,Xu W B.Particle Swarm Optimization with Particles Having Quantum Behavior[C].Proceedings of IEEE Congress on Evolutionary Computation,2004:325-331.
[2]Sun J,Xu W,Feng B.A Global Search Strategy of Quantum-behaved Particle Swarm Optimization[C].Proceedings of IEEE Conference on Cybernetics and Intelligent Systems,2004:111-116.
[3]方伟,孙俊,谢振平,等.量子粒子群优化算法的收敛性分析及控制参数研究[J].物理学报,2010,59(6):3686-3693.
[4]颜亮,姚锡凡,胡俊,等.用于车间作业调度的粒子群优化算法[J].管理技术,2009(6):115-119.
[5]李小华,熊禾根.基于粒子群算法的车间调度问题[J].信息技术,2009(7):19-21.
[6]Shi Y H,Eberhart R C.Empirical Study of Particle Swarm Optimization[C].Proceedings of 1999 Congress on Evolutionary Computation,Washington D C:IEEE,1999:1945-1949.
[7]EFGallad A,EFHawary M,Sallam A,et al.Enhancing the Particle Swarm Optimizer Via Proper Parameters Selection[C].Proceedings of the 2002 IEEE Canadian Conference on Electrical & Computer Engineering,Winnipeg:IEEE,2002:792-797.
[8]Sun J,Xu W B,Feng B.Man and Cybernetics[C].IEEE International Conference on Systems,Hawaii:IEEE,2005:3049-3049.
[9]范路桥,常会友,朱旭东.一种改进的作业车间调度算法及其实现[J].计算机集成制造系统,2005,11(5):673-677.
[10]何利,刘永贤,谢华龙,等.基于粒子群算法的车间调度与优化[J].东北大学学报,2008,29(4):565-568.
