一种基于小波的发动机数据融合算法

师伟，彭炬，谭世海，黎亮

一种基于小波的发动机数据融合算法

师伟1，彭炬1，谭世海2，黎亮2

(1.中国燃气涡轮研究院，四川江油621703；2.电子科技大学，四川成都611731)

航空发动机测试中，内部气流工况十分复杂，使用多传感器对同一截面进行测试表征一个面的气流状态，其结果往往有个别点不符合规律。为此，提出一种基于小波分析的解决方案。首先对发动机多传感器测试数据进行小波分频。然后从相似性、能量衰减等多个角度进行分析，指出高频和低频的不同特征，并提出对高频与低频部分使用不同方法进行融合的思路。最后总结出一种适用于航空发动机高空模拟试验数据使用的基于小波的数据融合算法。

航空发动机测试；数据融合；多传感器；小波分析；噪声；高空台

1 引言

高空台上的航空发动机测试，由于其环境复杂，往往采用多个传感器进行测试。测出的数据有时会在一个较大的范围内分布，极不均匀，用简单方法进行加权相加，往往不能很好地解释其意义，甚至得到有悖常理的结果[1]。按测量理论，传感器的测量值等于真实值与正态分布噪声之和，则当多个传感器数据相加后，噪声部分将相互抵消，融合值的偏离部分将逐步下降为0，这是多传感器融合的目的。大多数文献中，把融合方法的重点变成对各个传感器数据的赋权值过程，简单地对不同传感器给予大小不同的权重。这样做的后果是权重大的传感器的噪声在融合时占主导地位，因此融合后的噪声部分将难以消除。

检测和描述差异是数据融合的前提。传感器数据间的差异，有绝对差异但更偏重于相对差异[2～5]。在对差异的刻画上，基本使用线性或类似线性的方式来描述[6]。然而这些差异往往都是指数据序列间的整体笼统差异，没有考虑由于局部传感器环境对整体造成的固有差异。

数据特征分析是数据融合的另一个前提。小波分析是其中的一种重要手段[7]，当前在信号分析和滤噪中使用最多。在数据融合研究方面，文献[8]提出了使用小波方法对不同频段的发动机信号进行不同处理的思路，文献[9]使用小波方法对发动机中非稳定信号进行提取，文献[10]使用小波分解并基于贝叶斯聚类融合方法进行发电机故障监测。小波处理的重要应用是去噪，虽然去噪的方法非常多，但其基本思想都基于噪声主要存在于高频部分的一些数值较小的点中[11]。

不同传感器由于摆放位置及本身校准的差异，造成数据序列不同。进行融合时，一些文献首先把数据看成本来应该一致的随机序列的观点是有偏差的。本文认为，不同传感器序列不同是正常的。下面通过小波分析，分别使用Haar小波、Daubechie小波、Coiflet小波和小波包等不同方法处理，来分离数据中应相同的部分和不应相同的部分。

2 研究工具与方法

相似度(V-Shift)[12]是衡量两序列接近度的工具，长度为n的A、B两个数据序列的相似度可定义为：

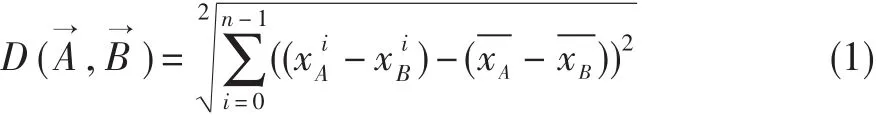
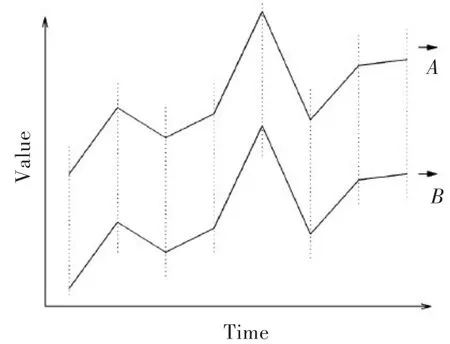
图1 V-Shift相似度很高的两个数据序列Fig.1 Two sequences of high V-Shift similarity

上式中相似度使用欧拉距离来度量。文献[13]中使用了数列的短期差异近似值，而非数列本身的值来进行差异比较，兼顾了两数列形态上的相似和距离上的相近。

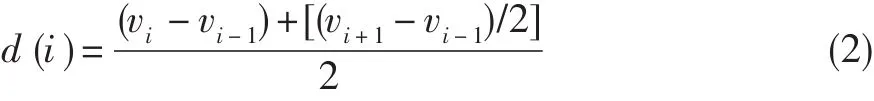
式中：vi为V-Shift相似度的值，d为两点之间的距离。

在衡量数据一致度时，使用动态时间弯曲(DTW)作为工具。在DTW的计算中，一般采用迭代计算方法的递归算法，后面对应点的DTW值不仅包含前面对应点的DTW值，也包含当前对应点的距离，是二者的加权和。式(3)中DTW可反复调用式(2)，能很好地描述两序列(包括平移错位后等)的整体差异。

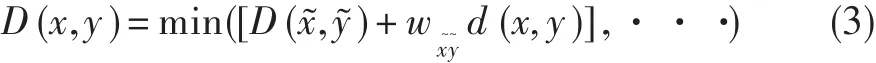
式中：x͂、y͂分别为x点和y点前面附近的点，w为权重，d(x,y)为两点的直接距离(包含欧拉距离等)。D(x,y)将从周围可达点列中搜寻最优值，其基本方法如图2所示。一般情况下，小波的支撑长度越长，反映低频的能力越强；支撑长度越短，越能体现高频的瞬间变化。

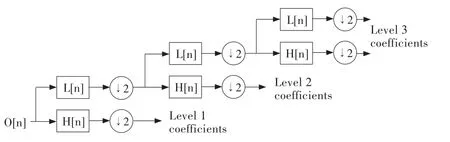
图2 小波分解Fig.2 The levels of the wavelet decomposition

3 测试信号的小波分析

研究中以离散小波为工具，把原始数据序列(用o表示)分解为高频部分(用h表示)和低频部分(用l表示)。通过计算观察序列oi、hi、li的特征及其之间的关系。以某发动机试验K6截面的15个传感器测试数据序列，和T23截面的21个传感器测试数据序列为研究对象，某次试验中测量数据见图3。由于T23有21个温度传感器，两两比较总共有C212=210次比较。同理K6有C152=105次比较。比较时，使用了支撑长度较短的Haar小波、支撑长度较长的Coif30小波和介于期间的其它几个Daub小波来进行分频。

分别从V-Shift距离差异、DDTW(导数动态时间弯曲)平均路径长度差异和相关系数3方面，对高频、低频序列进行比较，结果见表1～表3。

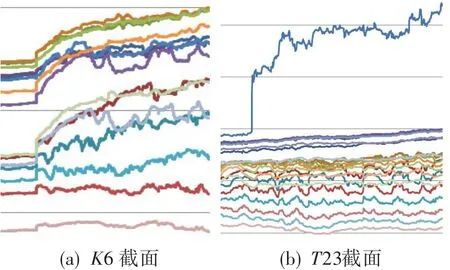
图3 K6和T23截面传感器测试数据Fig.3 Data from sensors onK6cross section and sensors onT23cross section

表1 K6和T23截面序列间V-Shift差异Table 1 The V-Shift difference between the sequences on K6andT23cross section

表2 K6和T23截面序列的DDTW平均路径长度/数列长度Table 2 DDTW path average length/sequence length of the sequences onK6andT23cross section

表3 K6和T23截面序列平均相关系数Table 3 The average correlation coefficient of the sequences onK6andT23cross section

表1体现了数据间基于欧拉距离的相似程度，由于此距离为排除两序列中心点差异后的差异，其结果说明高频数据间的距离关联度比低频的高。表2体现了数据间基于形态的相似程度(包括平移错位)，也说明高频数据间的形态关联度较高，即在距离和形态上，高频数据间的相似度要比低频部分大。表3使用了统计中常用的相关系数，其中低频结果与原始序列差不多，符合常规逻辑。高频结果中，支撑长度最短的Haar小波显示出非常明显的弱相关，而其它小波显示出较高的相关性。这说明Haar高频中的白噪程度较高，在支撑度长的小波中相互抵消后，高频序列变得稳定。故可通过支撑长度长的小波来判断整个小波序列是否有效，即若某传感器的高频同其它传感器的严重不一致，则该传感器有问题。支撑长度短的小波因抵消噪声程度明显，可作为噪声级别的监控指标。总之可认为，发动机系统在运行中，对各传感器在高频数据部分产生的影响较为相近，但对低频部分产生的影响则不尽相同，这主要是各传感器本身的内部或局部环境不同所致。经小波分频，可很好地区分传感器间的固有差异和系统造成的动态差异。

4 小波序列的能量

定义(EH/EL)/(FH/FL)为融合噪声衰减指数，反映各个同质传感器相加后，由于白噪声抵消而产生的高频能量衰减程度。

由表4可知，传感器越多，效果越明显。另外，Haar小波的高频部分对噪声最敏感，因为其支撑长度短，对噪声最灵敏；其它小波由于支撑长度长，噪声在本序列中相互融合掉了。由于支撑长度长的小波不易看出融合效果，故可考虑使用Haar小波检测分频的最佳层数。

表5反映了不同小波分频层数中噪声衰减的程度。可见，除Haar外，其它小波对层数不敏感。一般来说，随着层数的增加，越来越多的非噪声成分混入高频，融合能量的衰减将逐渐降低。T23每增加一层，其能量的衰减效果大幅减弱，说明噪声主要集中于第一层。K6中第一层和第二层的效果接近，而第三层的效果显著降低。说明对T23来说，一层分频就可用于滤噪；而对K6来说，高频可分到二层。

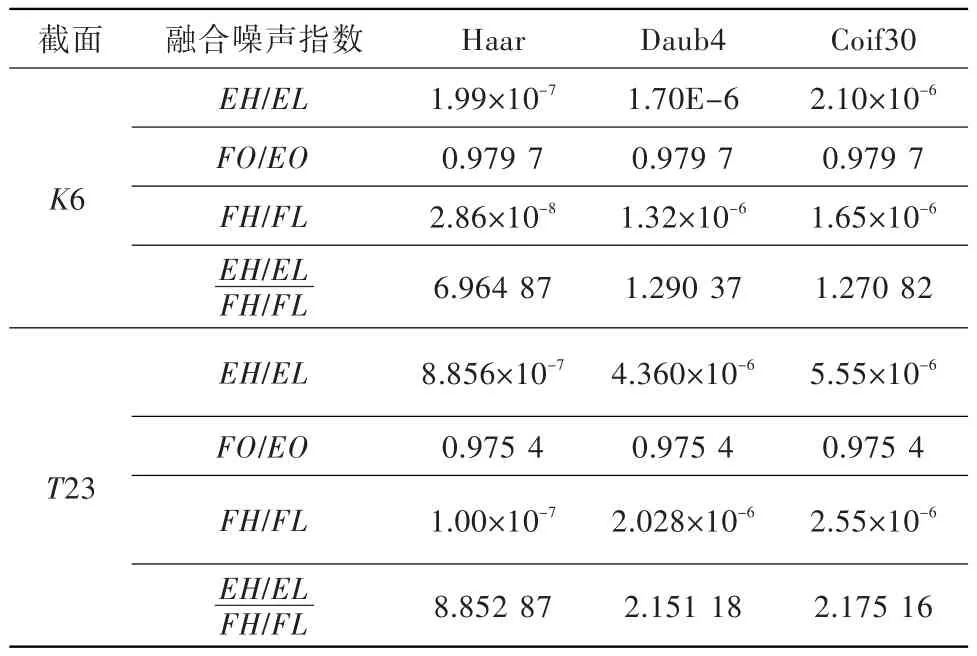
表4 K6和T23截面序列平均融合前后比较Table 4 The comparison of the energy index ofK6andT23 sequences before and after the data fusion

表5 K6和T23截面序列的融合噪声衰减指数与小波层数的关系Table 5 The relationship between the fusion noise attenuation index ofK6andT23sequences and the levels of wavelets

5 融合方案

5.1融合

根据上述分析，融合算法可总结为：

(1)用支撑长度较长的小波对各传感器序列进行一层分频，并对比各序列高频能量。假设各序列高频能量分别为ei传感器数量≥EMAX，其中EMAX为认为设定的一个能量异常阀值，说明该序列有问题，去掉EMAX值可为7～15，表示允许单传感器的高频能量超过平均值的7～15倍。支撑长度长的小波(如Coif30)，其能量集中性较好，故稳定性更好。

(2)把余下各序列平均相加，用Haar小波重新进行多层分频，计算各次的融合噪声衰减指数，分析结果。随着分层的增加，高频部分数据量增多，非噪声部分增加，融合噪声衰减指数的总趋势会下降(不排除个别地方会上升)。

(3)以第一层的融合噪声衰减指数为基点，在一个适当范围HC寻找最多可能到达的层次HL。建议HC＜10%，即在融合噪声衰减指数损失不大的情况下，找到一个合理的层次。表5中T23传感器组的层次为1，K6传感器组的层次为2。通过这种分频方式，可把噪声集中的高频层次分离出来，形成噪声序列和稳态序列两大部分。

(4)按照HL层次重新对各传感器序列进行分频。把高频部分相加平均，得到高频融合序列HD。HD中由于白噪得到综合，其能量有所下降。

(5)把上面分频得到的各低频序列按照策略进行融合，生成低频融合序列LD。

(6)高频融合序列HD与低频融合序列LD进行小波叠加，形成融合后的最终序列。

5.2计算实例

以T23的21个传感器数据序列为例。

(1)首先进行高频能量分析。用Coif30小波对21个传感器数据序列进行一层分频，结果如下:

0.001206028 0.0059696970.001214602

0.001988444 0.0031746040.000599434

0.975258864 0.0012242630.000201351

0.001779909 0.0003055250.000106791

0.002200573 0.0000594050.000067454

0.002557885 0.0000078350.000054308

0.001977464 0.0000014010.000044164

通过数据发现第7号传感器的能量显著大于其它传感器序列，于是认为第7号传感器异常，去掉第7号传感器序列。重新计算20个传感器序列都符合要求，结果为：

0.048746115 0.2412876130.049092682

0.080370400 0.1283134890.024228368

0.049483185 0.0081383630.071941665

0.012348918 0.0043163630.088944384

0.002401068 0.0027264110.103386497

0.000316669 0.0021950590.079926601

0.000056607 0.001785040

(2)把这20个序列相加平均后，形成的新序列用Haar小波处理，发现其融合噪声衰减指数随着层数的增加分别为8.85、6.87、3.58等。

(3)如果HC为10%，则处理层次为1。

(4)把20个传感器序列用Haar小波进行一层分频，把其中的20个高频序列相加平均，形成的高频融合序列HD如图4所示。

(5)参照文献[12]，把上一步形成的20个低频序列按常规方法融合成LD。

(6)把HD序列和LD序列分别作为小波的高、低频进行反向叠加，形成新的序列，即为融合后的最终序列。

图4 T23截面剩余20个传感器序列的高频融合结果Fig.4 The high-frequency data fusion results of the rest 20 sensors onT23cross section

6 结束语

传统数据融合方法是基于对数据序列的整体计算，小波分频则主要用于特征识别。本文的贡献在于把这两种方法进行了结合，并用于发动机数据融合中。对于传感器组的数据往往追求其一致性，但高频数据的一致性更多来自于能量的分配和强烈的随机性，而不是数据的均等。本文提出把低频和高频数据用不同方式来处理，低频强调其一致，而高频强调其相互抵消作用。对发动机数据序列的高频、低频进行多角度分析，提出一套基于小波分频的发动机数据融合方案，并给出了相应的(侧重于高频的)实例。在分析基础上进行小波高、低频分别处理的方法，也可用于发动机其它测试数据的融合分析。

[1]李军，锁斌，李顺.基于证据理论的多传感器加权融合改进方法[J].计算机测量与控制，2011，19(10)：2592—2595.

[2]万树平.基于最小一乘估计的多传感器信息融合方法[J].计算机工程，2010，36(2)：257—259.

[3]韩峰，朱镭，智小军.基于模糊理论的多传感器数据融合测量[J].应用光学，2009，30(6)：988—991.

[4]董九英.多传感器数据融合的主成分方法研究[J].计算机工程与应用，2009，45(33)：111—113.

[5]焦竹青，熊伟丽，张林，等.基于接近度的多传感器数据融合方法研究[J].压电与声光，2009，31(5)：771—774.

[6]周新宇，吉琳娜，李香亭.一种多传感器数据的一致性融合方法[J].伺服控制，2011，25(6)：57—59.

[7]白浪，雷旭升，盛蔚，等.基于小波滤波的无人旋翼机高度信息融合[J].北京航空航天大学学报，2012，38 (5)：659—664.

[8]Gaeid K S，Hew W P.Wavelet Fault Diagnosis and Toler⁃ant of Induction Motor[J].International Journal of the Phys⁃ical Sciences，2011，6(3)：358—376.

[9]Abdesh M，Khan S K，Azizur R M.A New Wavelet Based Diagnosis and Protection of Faults in Induction Motor Drives[C]//.Proceeding of Power Electronics.Specialists Conference.2008.

[10]Gang N，Achmad W，Jong D S，et al.Decision-Level Fu⁃sion Based on Wavelet Decomposition for Induction Motor Fault Diagnosis Using Transient Current Signal[J].Expert System Application，2008，35：918—928.

[11]陈建，任章.小波包结点阈值自适应消噪法[J].电子测量技术，2008，31(4)：1—4.

[12]Chan F K，Fu A W，Yu C.Haar Wavelets for Efficient Sim⁃ilarity Search of Time-Series:With and without Time Warping[J].IEEE Transactions On Knowledge and Data Engineering，2003，15(3)：686—705.

[13]Keogh E，Pazzani M.Derivative Dynamic Time Warping [C]//.KUMAR V，Grossman R.Proceedings of the First SI⁃AM International Conference on Data Mining(SDM’2001).Philadelphia，2001.

Multi-Sensor Data Fusion Method Based on Wavelets

SHI Wei1，PENG Ju1，TAN Shi-hai2，LI Liang2
(1.China Gas Turbine Establishment，Jiangyou 621703，China；2.University of Electronic Science and Technology of China，Chengdu 611731，China)

Multi-sensors are often used in engine tests.However the results sometimes are difficult to inter⁃pret especially when data are irregular distributed and even inconsistent because of the complex environ⁃ment.A new fusion way based on wavelet analysis was presented.The sensor data were divided into two parts:high frequency and low frequency areas,which were examined from various aspects such as similarity and energy attenuation.It is found that there are many different characteristics between the two parts,and it is necessary to use different fusion methods to hand them.Finally a fusion algorithm based on wavelets has been presented.

aero-engine measurement；data fusion；multi-sensor；wavelet analysis；noise；altitude test facility

V263.6

A

1672-2620(2013)05-0050-05

2012-11-14；

2013-09-09

航空基金(20101024)

师伟(1976-)，男，陕西人，高级工程师，硕士，主要从事航空发动机高空模拟试验测试研究。