基于模糊指数融合和正交基分解的发动机性能监控

李冬，李本威，孙涛，宋汉强，赵勇

基于模糊指数融合和正交基分解的发动机性能监控

李冬1，李本威2，孙涛2，宋汉强1，赵勇1

(1.海军航空工程学院研究生管理大队，山东烟台264001；2.海军航空工程学院飞行器工程系，山东烟台264001)

针对发动机性能监控过程中出现的单参数监控信息量不足和多参数容易矛盾的情况，提出一种发动机性能监控模糊指数融合方法。该方法基于滑动窗口参数均值和熵，采取有效的信息融合技术，建立表征发动机性能的模糊融合指数。利用神经网络方法，依据已确定的模糊融合规则推导出剩余决策规则。实例表明，模糊融合指数能很好地跟踪发动机性能缓慢衰退和突变两种情况。用正交基分解的方法对模糊指数进行重构预测，与线性拟合和二次拟合相结合的方法相比，其预测精度更高，能准确预测发动机的性能变化。

航空发动机；性能监控；模糊信息融合；正交基分解；决策规则；信息熵

orthogonal basis decomposition；decision-making logic；information entropy

1 引言

航空发动机长时间工作后，各部件老化将导致其做功能力下降，因此有必要开展发动机性能监控研究，对性能下降的发动机及时跟踪，为发动机视情维修提供指导[1，2]。文献[3]基于神经网络优化算法对发动机燃气温度裕度(EGTM)进行预测，并以EGTM的变化表征发动机性能变化，但EGTM只作为发动机性能下降的一个重要方面。单参数评估由于忽略了其它参数的影响，或参数间存在矛盾时，容易出现误判。相比之下，多参数综合评估法则相对客观、合理，可减少误判机率。文献[4]～[6]采用综合加权法，融合发动机多个参数得到性能综合指数，以此监控发动机性能状况。文献[7]和[8]提出基于支持向量机对发动机性能状况进行预测，但其参数选取过于依赖经验，不易直接获得。文献[9]采用回归树和模糊神经网络结合的方法对性能指数多步预测，取得了不错效果；文献[10]以最终误差预报准则优选嵌入维数，通过回归支持向量机预测发动机性能综合指数，并以此监控发动机性能。但两种方法同样存在回归参数难以确定的问题。文献[11]利用组合模型预测发动机性能指数，以免疫粒子群算法确定组合模型权重，较好地预测了短期的发动机性能指数变化。

本文在上述分析的基础上，通过构建表征发动机性能变化的参数数组和模糊隶属度函数，融合多参数信息对发动机状况进行评估。利用神经网络方法，依据部分已确定的规则推导出剩余决策规则，并将所有决策规则并入到模糊指数合成中。采用多参数模糊指数融合的方法，对发动机性能缓慢衰退及突变两种状况进行监控，判断发动机所处状况。采用正交基分解的方法对模糊指数进行重构预测，并与线性拟合和二次拟合相结合的方法进行对比。

2 构造性能参数监控的统计量

在实际发动机性能监控中，反映发动机运行状态的参数很多，但实际条件的复杂性，使得这些热力参数与发动机性能状态的对应关系具有一定的不确定性和模糊性。由于发动机性能衰退伴随使用时间的增加而逐渐增加，所以选择与飞行时间相关的性能参数作为表征发动机性能状况的参数。发动机监控参数的选择受传感器可安装数量及位置限制，本文确定低压转子转速n1、高压转子转速n2、涡轮后燃气温度T4作为发动机性能监控参数[11]。

为监控发动机性能状态，将各类参数按照滑动窗口进行处理，求取每一滑动窗口内数据的均值和熵，以此构造样本参数的统计量，即：

式中：k=n-r+1，n为参数时间序列长度，r为滑动窗口长度，mean()为取均值，entropy()为取熵运算，xik为i种参数(i=3，分别为n1、n2和T4)k个样本点的数值，sik为i种参数k个滑动窗口内参数的平均值，tik为i种参数k个滑动窗口内参数的熵。平均值反映发动机性能状况；熵表示滑动窗口内数据波动情况，对应性能变化程度。熵的计算式为：

式中：nikj为i种参数在第k个滑动窗口内j组内对应的个数，hik为i种参数在k个滑动窗口的信息熵，m为k个滑动窗口内参数的分组数，参数按等分分组。

当发动机性能缓慢衰退时，滑动窗口内样本均值和熵缓慢变化；当发动机性能突变时，样本均值和熵相应会出现突变。当参数非均匀变化时，对应的熵减小。直观看，这两个统计量能反映发动机的性能状况。

随着使用时间的增加，发动机会出现性能下降。一般来讲，n1和n2随飞行时间的增加而逐渐偏离正常状态，T4则逐渐增加，数据变化趋势不同。如果对上述三个参数进行融合，会使融合结果出现矛盾，因此有必要对数据进行规范化处理。引入下列变换形式：

(1)效益型数据

式中：aik可为sik、tik，ai,mink为第i种参数的最小值，ai,maxk为第i种参数的最大值，a′ik为处理后的值。定性看，n1、n2平均值属成本型数据，T4平均值属效益型数据，三种参数的熵属成本型数据。

由上述分析可知，构造某一样本点表征发动机性能的参数数组形式为[s1k，t1k，s2k，t2k，s3k，t3k]，s1k、t1k、s2k、t2k、s3k、t3k分别表示在第k个样本点的平均值和熵。

3 多参数模糊指数融合

采用多参数模糊指数融合方法，监控发动机性能状况。通过构建输入和输出隶属度函数，将输入参数转化为反映发动机性能的指标。每个输入对应四种状态，输出对应三种状态。构造的隶属度输入、输出函数[12]如图1所示。

分析图1可知，输入模糊集定义为：ZV：零值，SV：小值，MV：适中值，BV：大值。输出模糊集定义为：NR：正常范围，MR：中间状态，AR：不正常状态。其中，输入参数0～0.33表示ZV～SV，0.33～0.66表示SV～MV，0.66～1.00表示MV～BV。输出参数0～0.50表示NR～MR，0.50～1.00表示MR～AR。

图1 输入、输出参数的隶属度函数Fig.1 Membership functions for input and output parameters

定义输入和输出隶属度函数后，结合模糊决策规则(依据学习和领域专家经验得到)，才能将输入参数融合，得到模糊融合指数。研究中，所得诊断规则基本与专家经验相一致[13]。本文总结了相关决策规则，这些规则以IF(输入参数的表示范围)、THEN(发动机所处的性能状况)表示。输入模糊集中每个参数对应四种不同的状态。表1列出了部分决策规则。

表1 部分决策规则Table 1 Part of decision-making logic

以表1第1条决策规则为例进行分析可知，当s1、s2、s3分别处于ZV、ZV和SV状态时，发动机性能处于正常状态。这些决策规则构成判断发动机性能的基础。模糊输入集有6个参数，这样一共会产生46个决策规则。通过以往经验及理论分析，能得到大部分决策规则，只有一部分规则未知。考虑到神经网络方法处理非线性问题及泛化的能力[14]，即使不是样本集中的输入也能给出合适的输出。以确定的决策规则作为训练样本，其中输入标记集为6参数(形式同性能变化参数数组)，输出标记集为3参数。此时，神经网络的输入和输出标记集中的参数为标记符号。本文约定：输入标记集中的ZV：0，SV：1， MV：2，BV：3；输出标记集中的NR：0，MR：0.5，AR：1。注意到图1(b)，输出标记集的参数对应两个隶属度，即输出参数具有模糊性。但结合确定的模糊规则，只存在唯一的隶属度。利用下述模糊融合算法求解模糊指数。

由图2可知，模糊输入集中每个参数对应2个数值，6个参数对应12个点。这12个点至少会产生26=64个规则(如果存在模糊规则)。模糊指数融合及预测流程如图3所示。

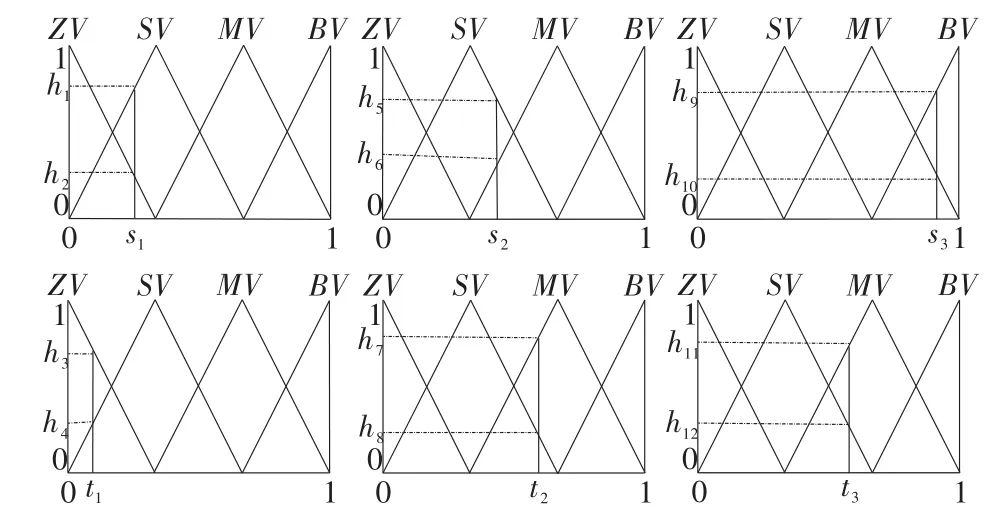
图2 输入参数的模糊集合Fig.2 Fuzzy set of input parameters

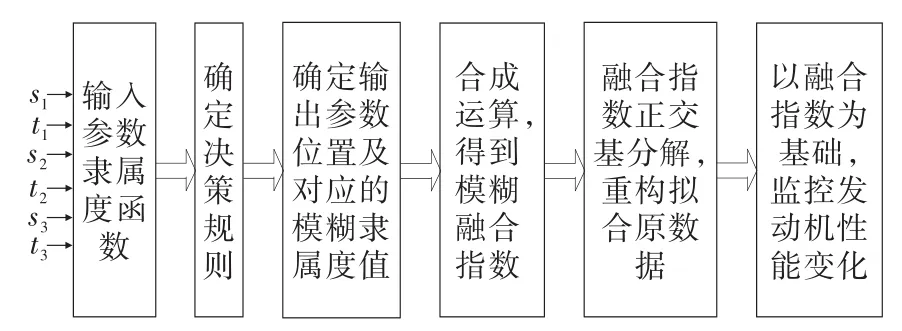
图3 模糊指数融合和预测流程Fig.3 Flow chart of fuzzy index fusion and prediction

根据图3中的计算流程，模糊指数融合及其预测算法流程总结为：

Step1：原始数据经滑动窗口和规范化处理，确定参数数组[s1、t1、s2、t2、s3、t3]。

Step2：模糊指数集合有64种组合，可产生64个决策规则。对于某一确定的规则，依据模糊合成运算，得到模糊输出参数位置。其中，某一规则对应输出参数的模糊合成计算式为：

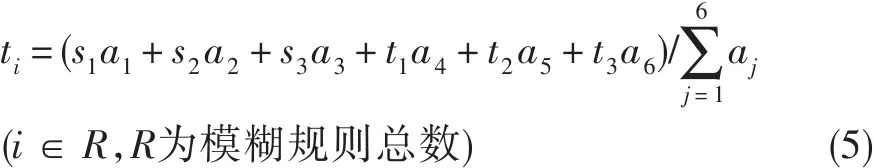
式中：a1∈{h1，h2}，a2∈{h5，h6}，a3∈{h9，h10}，a4∈{h3，h4}，a5∈{h7，h8}，a6∈{h11，h12}，t为模糊输出参数。

Step3：对于某一输出模糊集，根据决策规则都会产生相应的隶属度值，再根据式(6)得到模糊融合指数。

式中：index为模糊融合指数，b为输出参数对应的隶属度。

Step4：在得到的模糊融合指数基础上，利用正交基分解[15]的方法对指数进行重构预测。取部分数据进行训练，建立预测模型，并利用剩余数据验证所建模型。

由式(4)、式(5)可看出，模糊融合指数在0～1之间变化。接近0代表发动机性能处于正常状态，接近1则代表性能接近故障状态。

4 实例分析

a、b两台发动机的性能参数变化过程如图4所示，图中纵坐标经滤波后除以最大值进行归一化处理。实际中，发动机a性能逐渐衰退，无突变情况。而发动机b约在第45个样本点性能出现较严重问题，后经一段时间排除，性能得到恢复。

分析可知，图4(a)中参数随样本点缓慢增加，表征发动机性能缓慢衰退；图4(b)中低压转子转速约在第45个样本点附近出现突变，但又很快恢复到平稳状态，其它2个参数变化较平稳，未出现突变。这样就出现了相互矛盾的情况，各参数之间看似相悖，不易对发动机性能做出准确判断。

图5从熵的角度分析发动机性能状况。其中，发动机a 3种参数的熵基本保持恒定，表征性能变化平稳；而发动机b的低压转子转速熵在第45个样本点附近骤降，其它2种熵基本不变。3种参数的熵同样出现了矛盾，不能正确判断发动机性能状况。

以模糊融合指数分析发动机性能状况。首先求取滑动窗口内三种参数的均值和熵。经规范化处理后，作为模糊指数合成隶属度函数的输入。其中，n1、n2的平均值采用式(4)规范化处理，T4的平均值采用式(3)规范化处理；3种参数的熵均用式(4)规范化处理。按照模糊指数融合算法，得到模糊指数。考虑发动机性能缓慢衰退和运行过程中性能突变两种情况，跟踪对应模糊融合指数的变化，结果见图6。

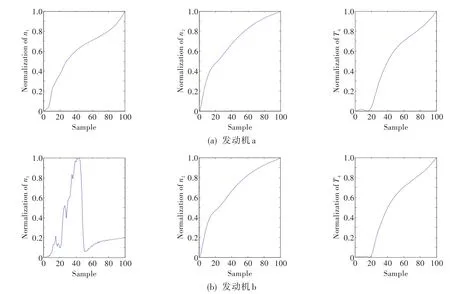
图4 发动机原始参数变化过程Fig.4 Original parameter variation of engine

由图6(a)可知，根据发动机性能模糊融合指数判断，发动机在1～40时间点性能衰退速率较快，近似成直线趋势；在45～75时间点内变化速率平稳，指数维持在0.6附近，表征发动机性能在这一段时间内基本稳定。实际中，发动机在初始阶段呈加速衰退趋势，但部件经一段时间磨合后，性能变化较稳定。图中曲线走势与实际性能参数缓慢衰退过程相符。图6(b)的模糊融合指数表示，发动机性能约在第45个样本点附近出现突变，且指数很大，接近0.8，预示出现较严重问题，与实际情况相符。经维修后，相对以前性能得到一定改善，因此第45个样本点后状态较平稳。

图5 发动机参数的熵Fig.5 Stable entropy of engine parameters

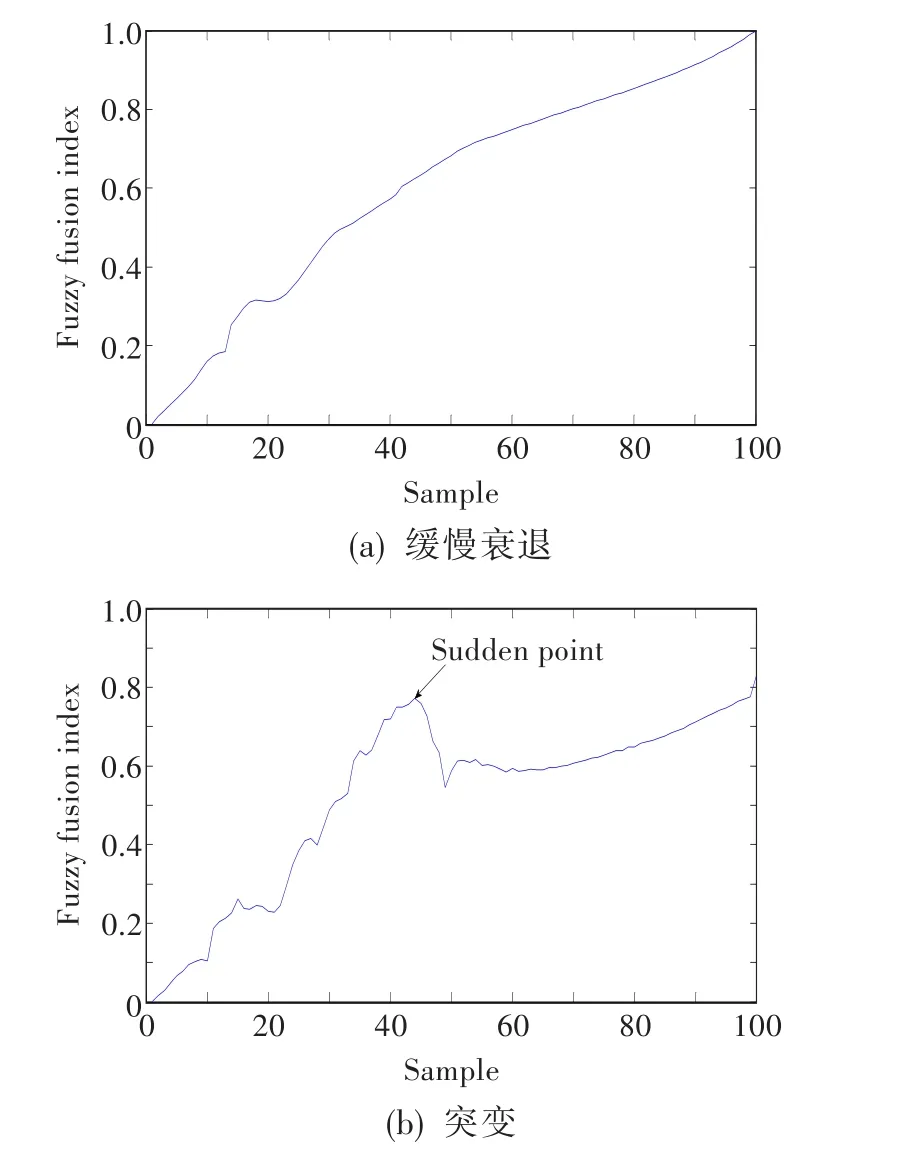
图6 发动机性能变化情况Fig.6 Changes of engine performance

采用正交分解的方法对发动机性能状态进行预测，同时引入文献[16]的线性拟合与二次拟合相结合的预测方法作比较分析。文献[16]预测问题的关键是选取线性预测和二次预测转折点，借助偏度统计量，当数据偏度出现连续增大或减小时，应改变拟合模型(拟合系数)。以下面两种判别标准判断预测精度。

(1)误差的标准差(rsm)

(2)相对误差的最大值(rmax)

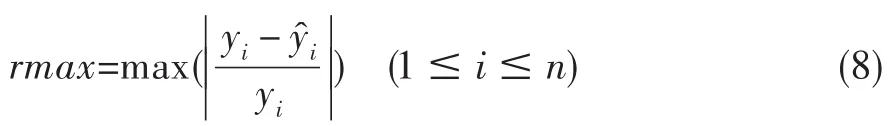
式中：n为预测数据个数，yi为模糊融合指数实际值，为预测值。

本文建立100组统计样本，前80组进行训练，建立预测模型，后20组数据验证模型。由于模糊融合指数{yi}包含近似线性趋势项，通过一阶差分法将趋势项直接剔除，从而得到平稳时序{∇yi}，其表达式为∇xi=xi-xi-1。对{∇xi}建立预测模型，再根据差分关系还原得到{xi}的预测模型[17]。两种预测结果如图7、表2所示。

由图表中可知，正交基分解方法在误差的标准差和在相对误差最大值两项指标上都优于文献[16]中方法。据此可认为，正交基分解方法能对模糊融合指数进行准确预测，从而更好地监控发动机性能。

图7 模糊融合指数预测结果Fig.7 Prediction of fuzzy fusion index

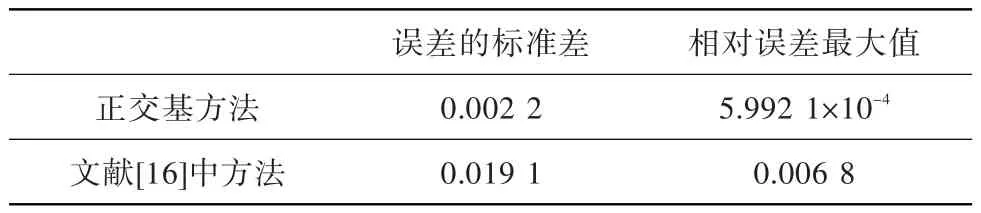
表2 预测结果对比Table 2 Comparison of prediction results

5 结论

本文基于收集的发动机测量数据，综合各测量数据的信息，将其融合成反映发动机性能变化的指数，并基于该指数监控发动机性能。该方法能克服单参数监控信息量不足及多参数监控容易矛盾的缺点，对发动机实施有效监控。主要研究结论为：

(1)基于模糊融合算法，构建了输入和输出参数的隶属度函数，并以此为基础进一步进行模糊融合，得到当指数接近0表征发动机性能正常，接近1表征发动机接近故障状态。模糊融合指数能很好地监控发动机性能缓慢衰退和突变两种情况。

(2)采用正交基分解方法对模糊融合指数进行重构预测，得到的融合指数能很好地判断发动机的性能状况，且该预测方法优于文献[16]中的线性拟合和二次拟合相结合的方法。

[1]李冬，浦鹏，谭巍，等.高压压气机性能老化预测和影响分析[J].燃气涡轮试验与研究，2011，24(4)：1—5.

[2]李冬，黄帅，曹明川，等.基于支持向量机的发动机性能衰退指标分类和预测[J].燃气涡轮试验与研究，2012，25(3)：20—25.

[3]张莹，左洪福，任淑红，等.一种航空发动机性能衰退预测的优化算法[J].中国机械工程，2011，22(9)：1009—1013.

[4]谢寿生.某型飞机发动机故障诊断与性能趋势监测研究[D].西安：西北工业大学，1998.

[5]胡金海，谢寿生.基于遗传算法的发动机性能监控与故障诊断[J].推进技术，2003，24(3)：198—200.

[6]胡金海，谢寿生，胡剑锋，等.基于粗糙集理论的航空发动机性能综合评判[J].系统工程与电子技术，2006，28 (5)：704—707.

[7]尉询楷，李应红，王硕，等.基于支持向量机的航空发动机滑油监控分析[J].航空动力学报，2004，19(3)：392—397.

[8]徐启华，师军.基于支持向量机的航空发动机故障诊断[J].航空动力学报，2005，20(2)：298—302.

[9]Tran V T，Yang B S，Tan A C C.Multi-Step Ahead Direct Prediction for the Machine Condition Prognosis Using Re⁃gression Trees and Neuro-Fuzzy Systems[J].Expert Sys⁃tems with Applications，2009，36(5)：9378—9387.

[10]胡金海，谢寿生，骆广琦，等.基于支持向量机方法的发动机性能趋势预测[J].推进技术，2005，26(3)：260—264.

[11]李冬，马力，樊照远，等.基于免疫粒子群优化的不等时间间隔发动机性能综合指数组合预测[J].燃气涡轮试验与研究，2013，26(2)：42—45.

[12]Boutros T，Liang M.Mechanical Fault Detection Using Fuzzy Index Fusion[J].Machine Tools and Manufacture，2007，47(11)：1702—1714.

[13]陈恬，孙健国.粗糙集与神经网络在航空发动机气路故障诊断中的应用[J].航空动力学报，2006，21(1)：207—212.

[14]徐士良.数值分析与算法[M].北京：机械工业出版社，2007.

[15]侯凤阳.基于人工神经网络的燃气轮机气路故障诊断研究[D].南京：南京航空航天大学，2007.

[16]Li Y G，Nilkitsaranont P.Gas Turbine Performance Prog⁃nostic for Condition-Based Maintenance[J].Applied Ener⁃gy，2009，86(11)：2152—2161.

[17]杨叔子，吴雅.时间序列分析的工程应用[M].武汉：华中理工大学出版社，1996.

Engine Performance Monitoring Based on Fuzzy Index Fusion and Orthogonal Basis Decomposition

LI Dong1，LI Ben-wei2，SUN Tao2，SONG Han-qiang1，ZHAO Yong1
(1.Graduate Students Brigade，Naval Aeronautical Engineering University，Yantai 264001；2.Department of Airborne Vehicle Engineering，Naval Aeronautical Engineering University，Yantai 264001)

Aiming at information shortage of single parameter and easy contradiction of multi-parameter in the process of engine performance monitor,a method of fuzzy index fusion in the engine performance moni⁃tor was presented.With effective information fusion technology,based on parameter mean and entropy of sliding window,performance fuzzy fusion index was established.Residual decision-making logic was de⁃duced by neural network according to pre-determined fuzzy fusion rule.Example indicated fuzzy index could track the engine performance slow deterioration and sudden changes.Fuzzy fusion index was recon⁃structed and predicted by adopting orthogonal basis decomposition method.Compared with combination of linear and quadratic prediction method,orthogonal basis decomposition method gets higher accuracy,and predicts performance change accurately.

aero-engine；performance monitoring；fuzzy information fusion；

V235.13

A

1672-2620(2013)05-0035-06

2012-10-17；

2013-10-11

李冬(1984-)，男，辽宁葫芦岛人，博士研究生，主要从事航空发动机状态监控、性能评估、性能预测技术研究。