池壁与池底固接的无盖圆形水池计算

熊晓瑜，李 琇

(四川省建筑设计院，四川成都 610017)

为避免文章过于冗长，一些公式的推导过程、微分方程的求解、待定系数的确定、内力的具体计算步骤及附录部分的公式推导及计算步骤等本文略去。

1 推导过程

在水压力作用下，池壁将变形如图1 中虚线所示。

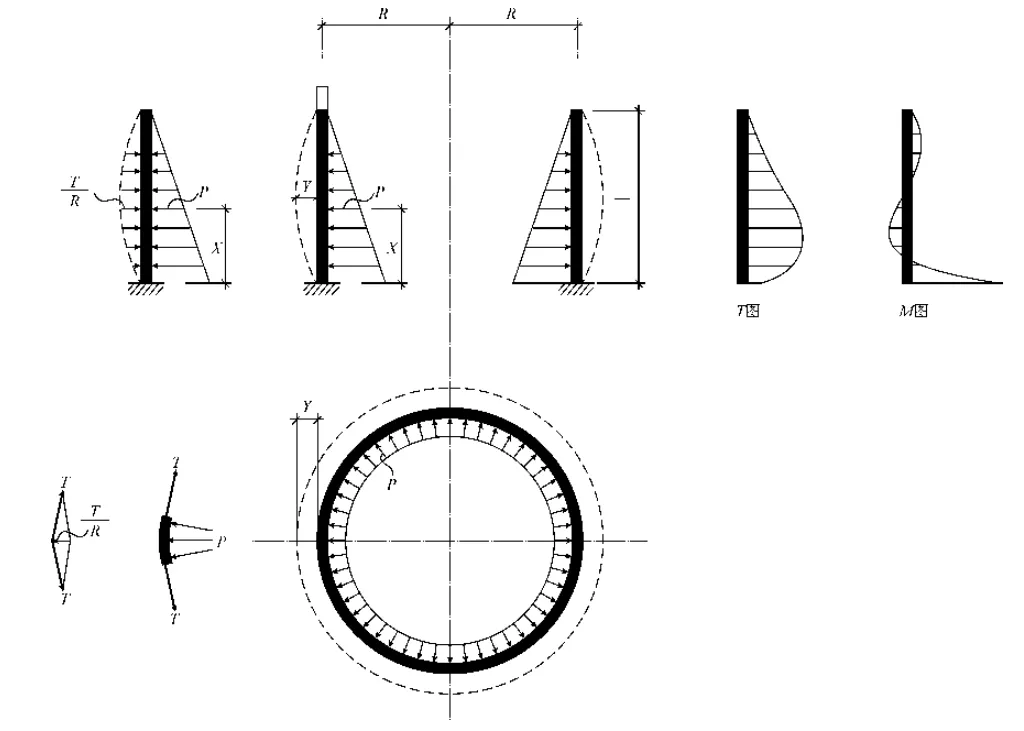
图1 圆形水池壁受力与变形

在距池底x 距离处切出单位宽度的圆环，在内部径向辐射形水压P 作用下，圆环将伸长，其半径也增大，设半径增大值为y，

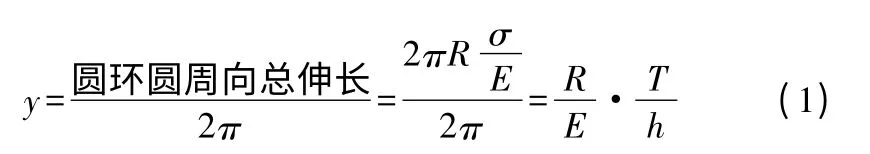
式中:E为池壁材料的弹性模量

h为池壁厚度

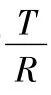
此悬臂梁应满足一般的弹性曲线微分方程:

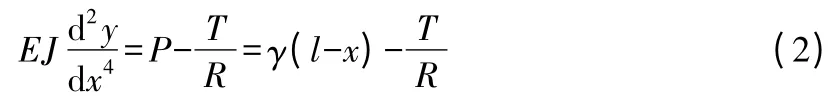
式中:γ为水的容重

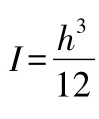
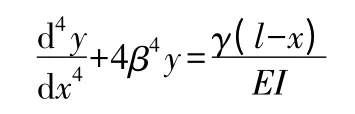
该方程的通解为:

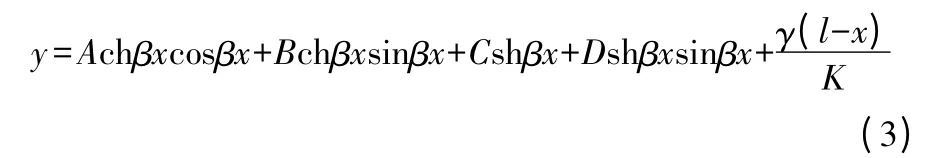
系数A、B、C、D 由边界条件:

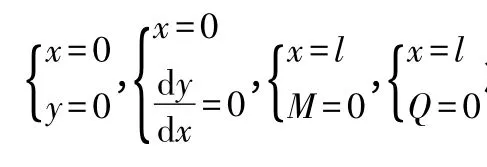
根据式(3)～式(6)及边界条件，可确定待定系数A、B、C、D，从而可求得任意点之内力。

实际应用中，可根据具体工程将数字代入后确定系数，不必先解出待定系数的一般公式。

2 计算实例

水池各部尺寸如图2 所示:

图2 水池尺寸

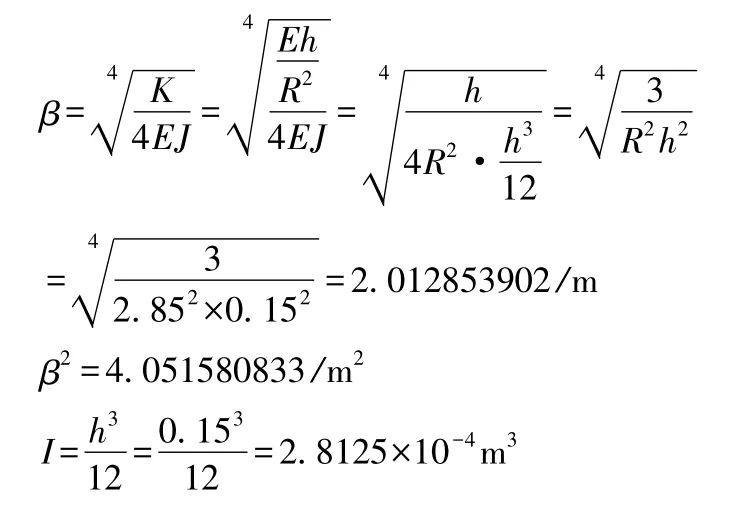
从而可求得池壁环拉力T 及垂直弯矩M 的结果见表1。环拉力图及弯矩图如图3 所示。

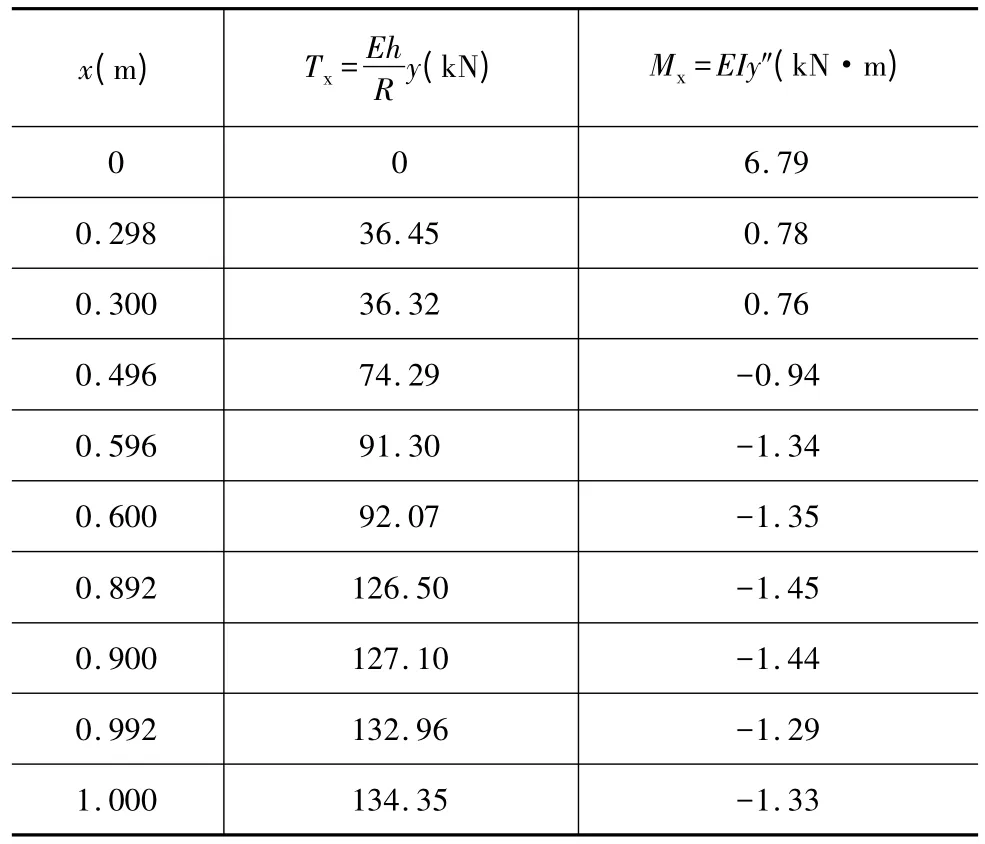
表1 实例计算结果

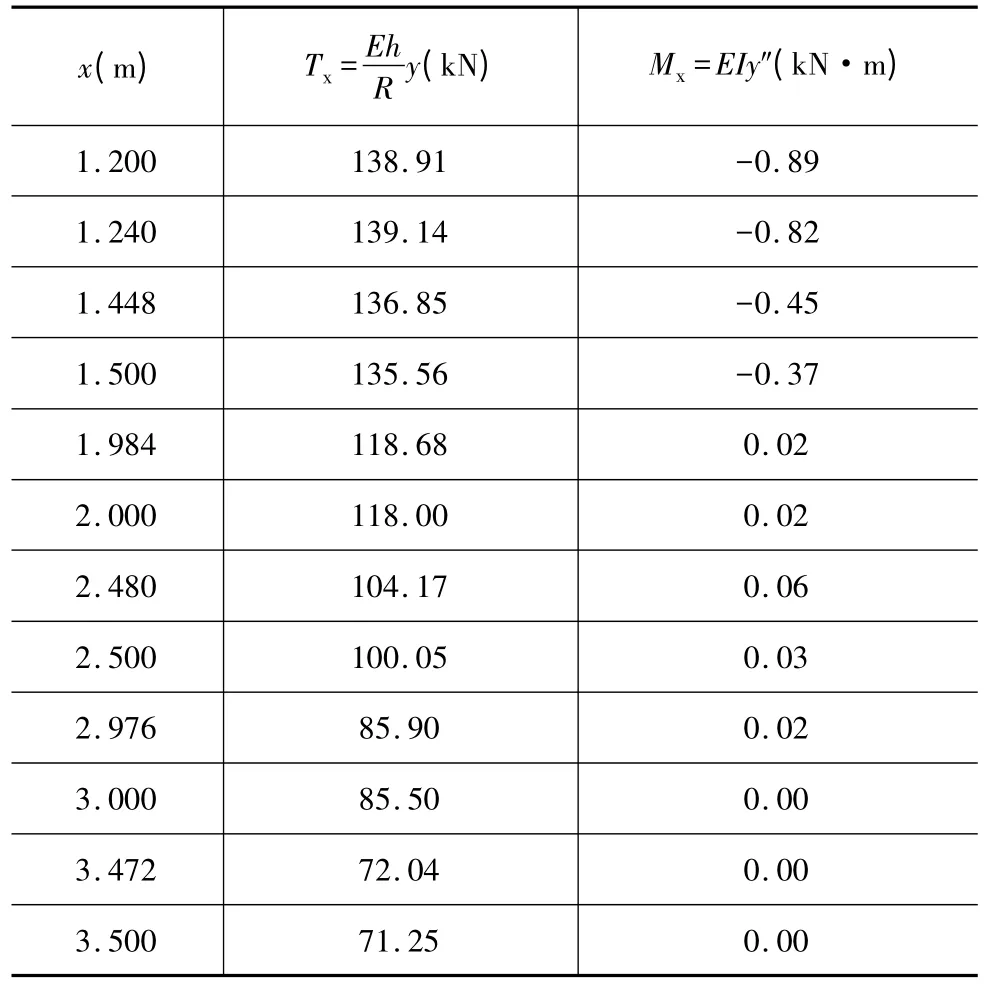
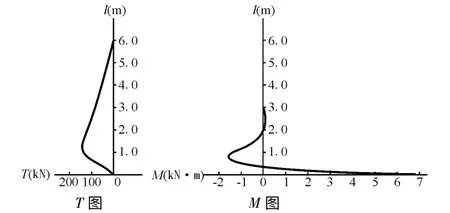
图3 水池壁环拉力及弯矩

3 结果检校

按帕斯捷尔纳克教授的方法计算的结果见表2。

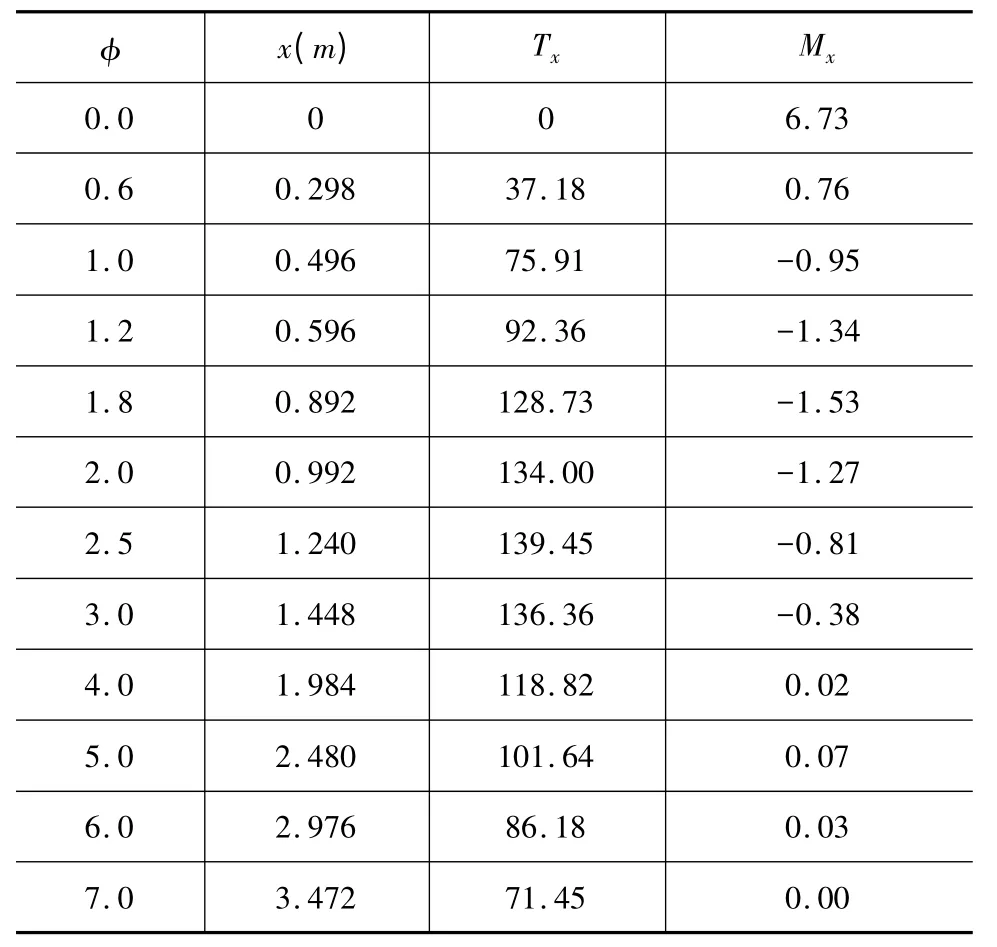
表2 帕斯捷尔纳克教授的方法计算的结果

4 结束语

从以上计算结果可见:两种方法所得结果非常接近，从而证明文中的计算公式是正确可靠的。

水池的配筋计算略。

［1］湖北给水排水设计院.钢筋混凝土圆形水池设计［M］.中国建筑工业出版社，1977

［2］同济大学数学教研室.高等数学(第三版)［M］.高等教育出版社，1988