二、三维耦合水动力模型研究I:模型的建立
2013-06-28黄玉新张宁川
黄玉新,张宁川
(大连理工大学海岸和近海工程国家重点实验室,大连116024)
二、三维耦合水动力模型研究I:模型的建立
黄玉新,张宁川
(大连理工大学海岸和近海工程国家重点实验室,大连116024)
利用基于非结构网格的有限体积法分别建立了二维和三维水动力模型。在实际工程应用中,二维模型一般用于模拟浅水自由表面流动,而三维模型在水流参数垂向结构变化较大时适用性更强。结合两者的特点,建立了二、三维耦合水动力模型。首先通过2个经典的算例来分别验证二维和三维水动力模型的精度和可靠性,最后通过一个潮流在斜坡地形上的传播实验来比较研究二、三维耦合水动力模型的实用性。结果表明,耦合模型在保证计算精度的同时,可有效提高工作效率。
耦合模型;二维水动力模型;三维水动力模型;非结构网格;有限体积法
随着海岸河口附近区域工程建设的需要,水动力数学模型得到了很好的发展。李孟国[1-2]、李蓓[3]、张青玉[4]和谭维炎[5]等分别建立了二维潮流模型,并很好地应用于相应的工程。Song[6]利用二维浅水方程建立了溃坝水流模型。近年来,三维水动力模型成为研究、应用的热点。窦振兴[7]对渤海的三维流场进行了模拟;李孟国[8]利用三维潮流模型对伶仃洋海域进行了研究;POM[9]、FVCOM[10]、ROMS[11]等开源模式的出现,使得三维水动力模型在工程中的应用更加广泛。但在实际工程应用中,由于缺少实测资料,同时为减小开边界的反射效应影响,模型范围定义远大于所研究的工程区域。特别是当需要进行三维模拟时,计算耗时将远远超过人们可以接受的预期。近年来,一、二维耦合模式和二、三维耦合模式因为计算效率相对较高越来越受到人们的关注。Miglio[12]、YANG[13]、Mahjoob[14]、张大伟[15]、王智勇[16]等将一、二维耦合模型应用于河道水流的模拟。王桂芬[17]首次提出了二、三维嵌套数学模型的概念,并成功应用于天津新港抛泥区的潮流计算。Namin[18]和Zounemat[19]也建立了耦合的二、三维水动力模型,但是后者耦合方式与前两者有所不同,他将水体表面采用浅水方程二维计算,而深水水体采用三维模型计算。Kilanehei[20]利用二维浅水方程耦合瑞雷平均的NS方程建立了适用于河道水流计算的水动力模型。一、二维耦合模式的应用已经十分广泛,而二、三维耦合模式除上述提及的研究者外,还少有这方面的研究成果,并且现有的二、三维耦合水动力模型在应用的全面性上有所欠缺,只能适用于特定情况的水流计算。本文在前人研究的基础上,建立一个能够考虑干湿界面变化、质量守恒的、有较强通用性的二、三维耦合水动力模型。
1 数值方法
1.1 二维水动力模型
采用沿水深平均的浅水方程作为二维水流运动的控制方程。守恒形式的浅水方程[21-22]如下

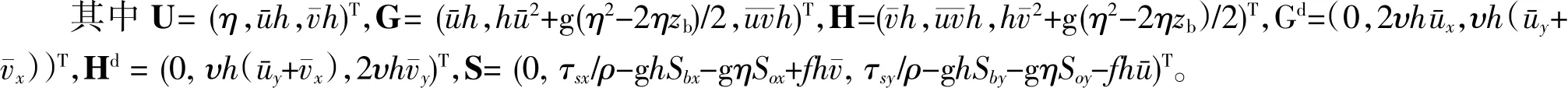
式中:η为水位;h为水深;ū、v分别为x和y方向的平均流速;g为重力加速度;ρ为水体密度;υ为水平涡粘系数;分别为x和y方向的表面切应力。
天然水域边界复杂,本文在非结构网格(三角形、四边形)基础上,采用单元中心格式的有限体积法对控制方程进行离散[23],运用高效的HLLC[24]黎曼格式计算单元界面对流通量。为增加格式的稳定性,对底摩阻源项进行了半隐式离散[25]。最后利用4步龙格-库塔法[26]和最小二乘线性重构法[27]建立了在时间和空间上都有二阶精度的二维水动力模型,具体的离散过程参见文献[23]。
在进行实际浅水非恒定流计算时,常会有干湿边界的存在。如潮间带的潮位涨落、溃坝和洪水演进等。二维水动力模型利用具有零质量误差的水位判别法[23]对干湿边界进行捕捉。
1.2 三维水动力模型
基于静压和Boussinesq假定的三维雷诺时均Navier-Stokes方程为三维水动力模型的控制方程。为更好地拟合地形起伏和水面波动,将方程在垂向上进行σ坐标转换,得到以向量形式表示的控制方程如下
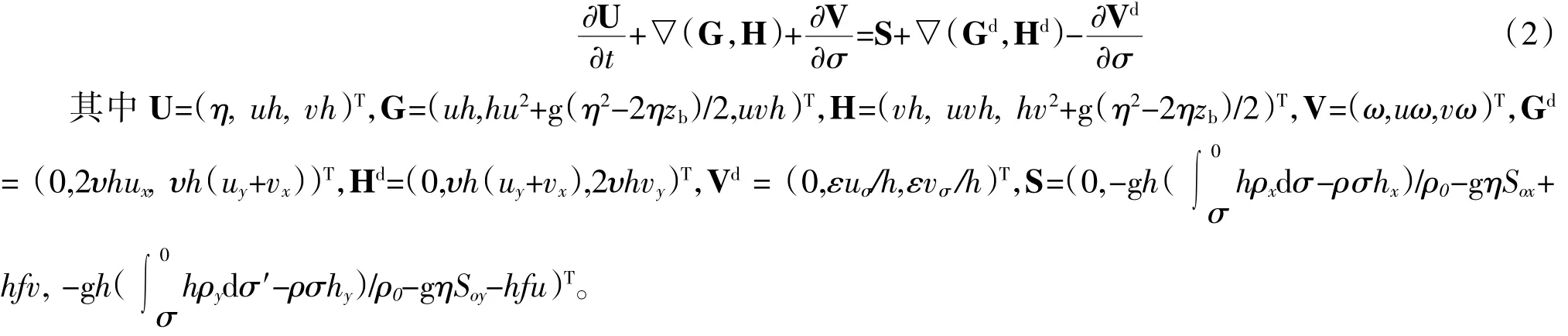
三维水动力模型在水平方向上采用与二维模型相同的网格划分。考察式(2)中的水平对流项(G、H)、水平扩散项()和底坡项(),这些项与式(1)相比有着相同的表达形式,因此它们的离散方式同1.2节中二维情况[23]。为了提高模型在垂向上对间断的捕捉能力,垂向对流项(V)的离散采用具有二阶精度的TVD格式[28],而垂向扩散项(Vd)利用隐式方法进行处理。模型耦合了时下流行的GOTM湍流模式[29],以闭合方程组。三维模型采用与二维模型同样的方法[23]来进行变量的空间二阶重构和时间二阶积分,以建立三维水动力模型。三维水动力模型采用与二维模型同样的方法进行干湿界面模拟。
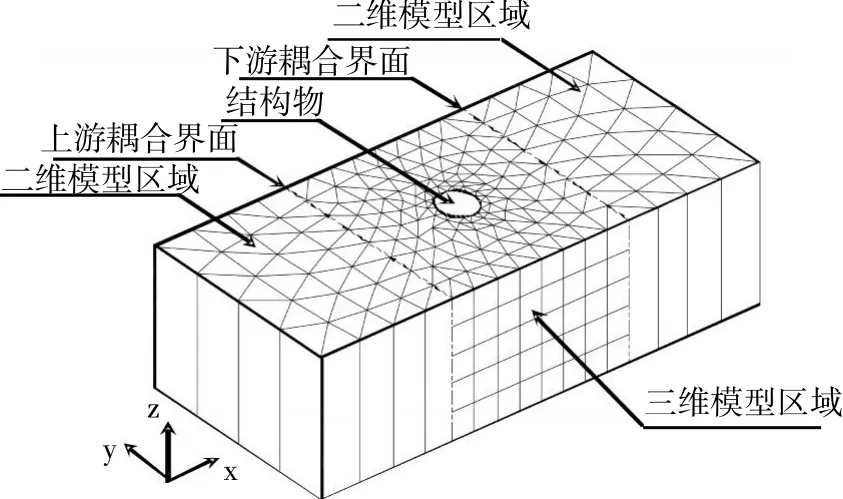
图1 二、三维耦合水动力模型的网格布置Fig.1 Grid layout for 2D-3D coupled hydrodynamicmodel
1.3 二、三维模型耦合方法
如图1所示,模型计算区域在平面上区分为二维和三维部分,两种区域通过耦合边界面相连,三维区域在垂向上采用σ坐标进行分层,而二维区域不考虑水流结构的垂向分布。为计算耦合界面上的通量时,二维和三维模型需要在界面上进行速度和水位变量信息的传递(图2)。本文采用由Van Rijn[30]提出的流速对数分布公式将沿水深平均的流速进行垂线化分布(式(3))。如图3所示,利用二维单元中垂线化分布后各分层流速与三维单元各分层流速在耦合界面上形成黎曼问题,通过HLLC格式计算界面上各分层通量,提供给三维单元积分使用。最后将通量进行垂向平均得到,供二维单元积分使用。
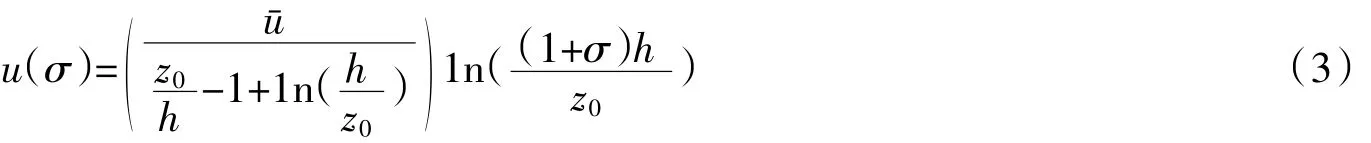
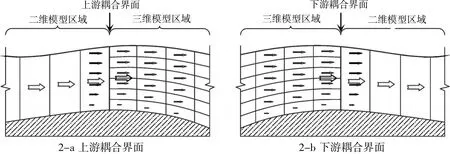
图2 二、三维水动力模型的耦合界面示意图Fig.2 Sketch of interfacial boundary between the 2D-3D hydrodynamic coupledmodel
在二、三维耦合水动力模型建立的过程中,三维模型的区域大小是一个值得讨论的问题。按照本模型建立的初衷,在感兴趣或工程需要区域进行三维模拟。然而在水平流速垂向分布后,其与三维模型的流速垂向分布可能存在差异。其原因是流速垂向分布公式并不能够完全真实的反演所有形式的水流。因此,耦合边界的定义需要离工程区域有足够的距离以减小这一影响。同时,还应注意地形变化对流速垂向分布的影响,建议耦合边界还应选择在地形平缓的位置。
二维和三维模型采用相同的时间步长,由于模型采用显示时间步进方法,时间步长受到CFL条件的限制。为了提高计算效率,本文采用动时间步长的处理技术[23],即根据CFL条件计算出每一时间步进时最合适Δt。下文的算例中,CFL=0.8。
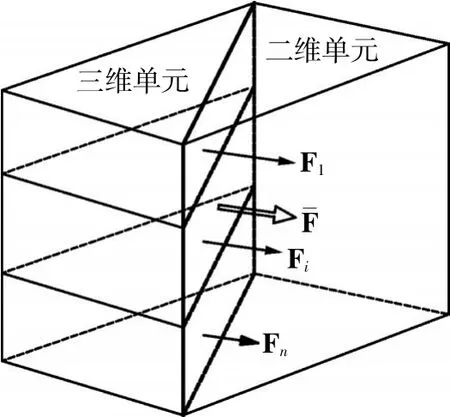
图3 耦合界面通量计算示意图Fig.3 Sketch of flux computation on interfacial boundary
2 模型验证
本节首先通过潮致环流算例和风生环流算例分别验证二维和三维水动力模型的精度和可靠性,最后通过一个潮流在斜坡地形上的传播实验来比较研究二、三维耦合水动力模型的实用性。
2.1 二维模型的验证
该算例研究潮波在矩形港池内的传播和作用。实验地形如图4所示(1 156个三角形单元),水深h=10 m,长L=3 400 m,宽B=1 500 m。在港池右边开边界处有振幅A=0.5m,周期T=12 h的余弦式潮波作用。港池底部和侧壁为滑动边界条件,不考虑科氏力影响。
根据Ippen[31]推导的理论解,距离左边界x的潮位和流速的解析表达式为

式中:A为潮振幅;ω为频率,ω=2π/T;h为水深。
模型采用冷起动的方式进行计算,图5给出了经过一个潮周后港池中心处水位和流速的数值模拟结果。从图中可以看出,数值解与理论解吻合很好。二维水动力模型准确地模拟了潮波在港池内的传播情况。
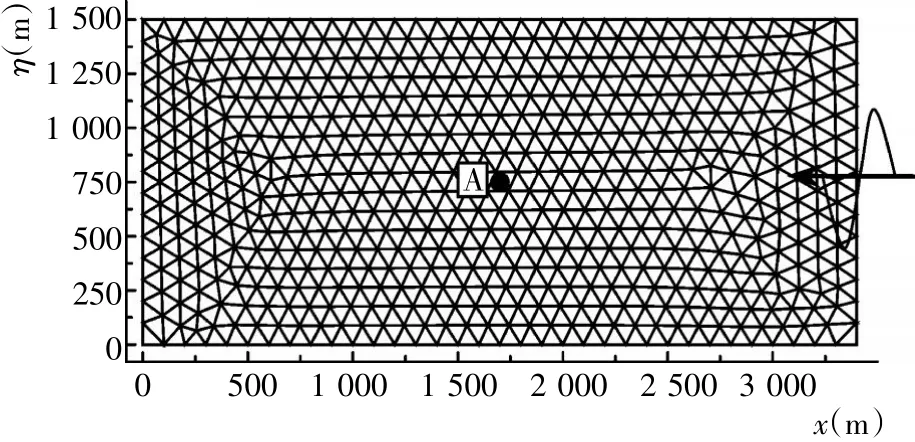
图4 潮致环流模型网格布置Fig.4 Mesh used for simulation of tide-induced circulation
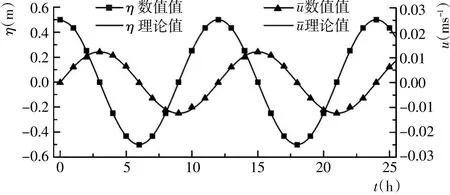
图5 验证点A处潮位和平均速度实验结果Fig.5 Numerical results of surface elevation and depth-averaged velocity at point A
2.2 三维模型的验证
风生环流算例主要用来考验三维水动力模型对流场垂向分布的模拟能力。实验范围为一长L=2 000m,宽B=800 m,水深h=10 m的封闭矩形水池。水面加载一个恒定的风应力τsx=1.5 N/m2,风向沿x轴正向。计算区域在水平方向由358个三角形单元剖分组成(图6),垂向等分为10层。模型不考虑科氏力的影响,水池底部采用无滑移边界条件,侧边界为滑移边界条件。水体密度ρ=1 000 kg/m3,垂向涡粘系数ε=0.01 m2/s。该恒定流在水池中心处(A点)的水平流速沿垂向分布的解析解[32]为

图7给出了A点处水平流速垂向分布数值解和理论解的对比结果,数值实验结果相对误差小于1%。三维水动力模型准确的模拟并得到了回流区的流速分布。
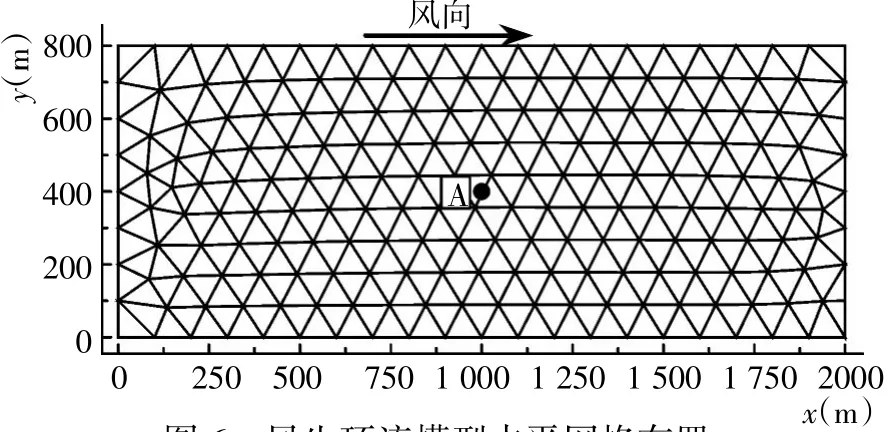
图6 风生环流模型水平网格布置Fig.6 Horizontal mesh used for simulation of wind-induced circulation
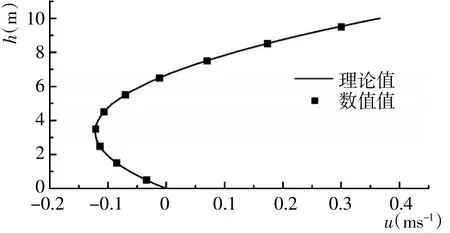
图7 验证点A处水平流速垂向分布与理论值比较Fig.7 Comparison of analytical and computed horizontal velocity profile at point A
2.3 二、三维耦合模型的验证及与三维模型的比较
实验范围和地形如图7所示,本次实验不考虑科氏力作用。在模型左边有一振幅为0.5m的S2潮波作用,其他各侧边界为固壁边界。二维模型中,底部糙率n=0.026,而三维模型垂向分为6层,底部采用无滑移边界条件。其中二、三维耦合模型的区域定义如图7所示。在模型的浅水区域分别设有6个测点(图8中的三角形,从左到右分别为P1~P6),以对比分析实验结果。
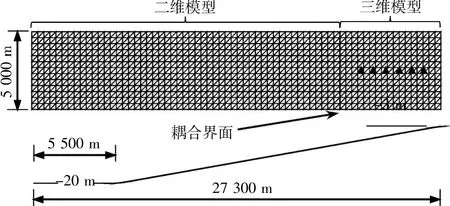
图8 数值实验的网格及地形Fig.8 Horizontal mesh and topographic of numerical experiment
为验证耦合模型的正确性和实用性,分别开展了整体二维、整体三维和二、三维耦合模型数值实验。图9给出了3种模型在2个潮周期内沿水深平均的水平速度对比结果。结果显示,耦合模型得到了与三维模型和二维模型相同的实验结果。因此,可以说明本文建立的耦合模型有着很好的计算精度。同时,图10中对三维模型和耦合模型在涨潮和落潮时各测点上水平流速垂向分布结果进行了对比,由结果可以看出,耦合模型的表层流速稍小于三维模型,但是相对量小于3%(P1测点表层),满足工程精度要求。随着水深的减小,两者的相对差值也随之减小。
将本次实验中以二维模型所需计算时间为单位1,三维模型计算所需相对时间为4.27,二、三维耦合模型计算所需相对时间为2.48,即本次实验中,二、三维耦合模型计算效率较整体三维模型提高了72%。多次的实际计算也证明本文建立的二、三耦合水动力模型有着很好的计算效率。
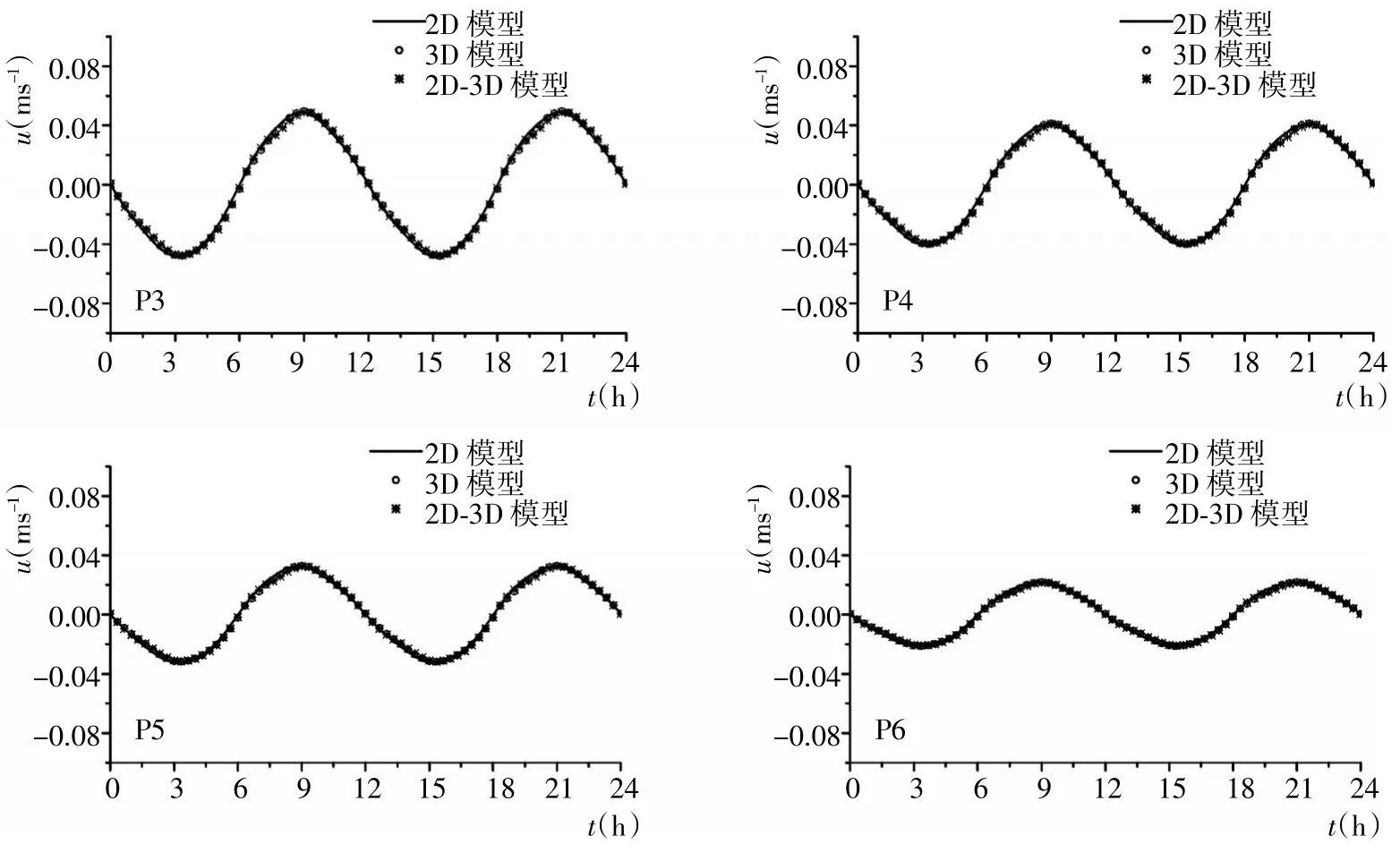
图9 各测点上3种模型水平平均流速数值结果对比Fig.9 Comparisons of numerical results of 2D,3D and coupled model for depth averaged horizontal velocity at locations P1~P6
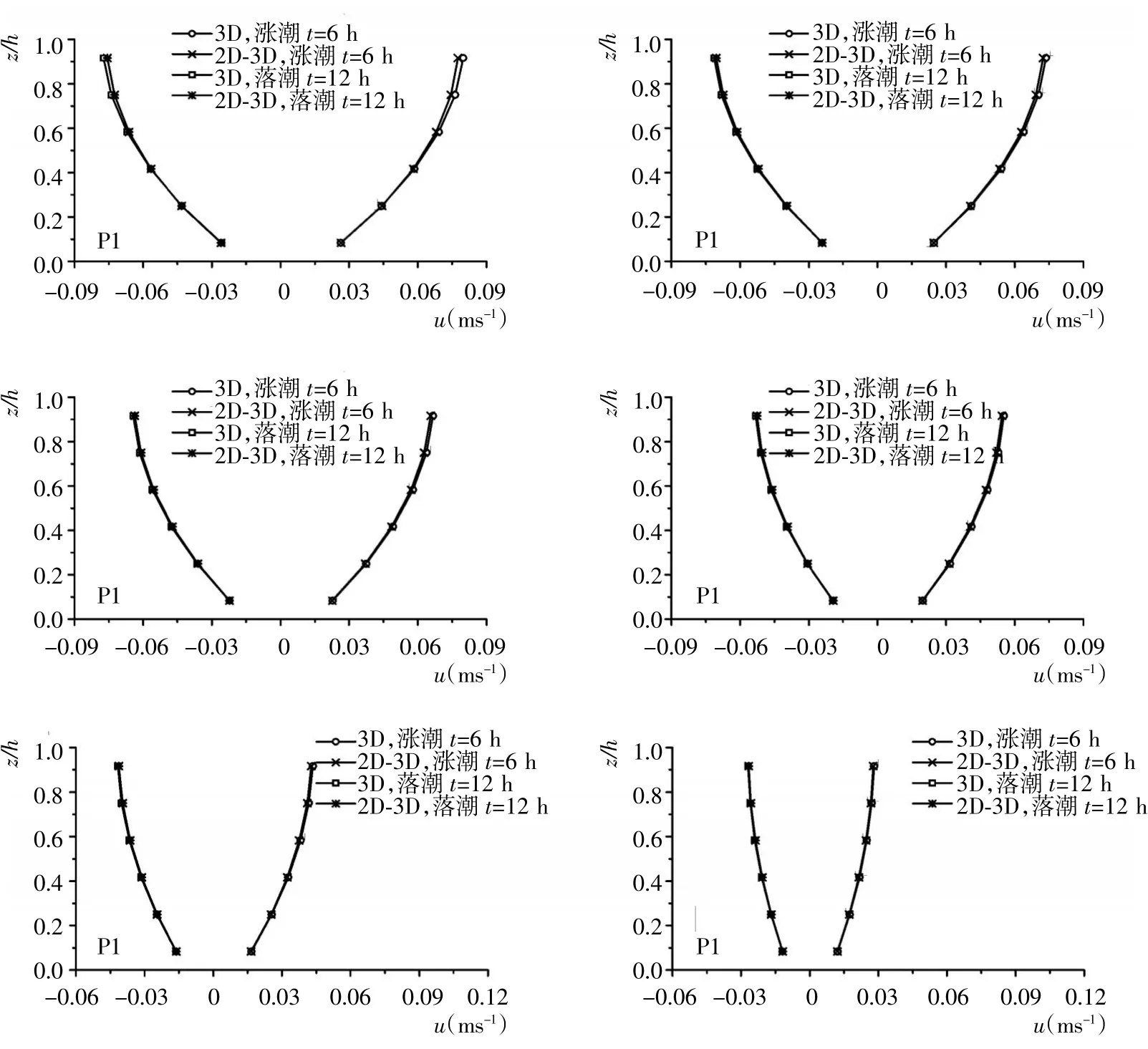
图10 各测点上三维和耦合模型的水平流速垂向分布数值结果对比Fig.10 Comparisons of numerical results of 3D and coupled models for streamwise velocity profiles at locations P1~P6
3 结论
本文在非结构网格的基础上,利用单元中心格式的有限体积法建立了在时间和空间上具有二阶精度的二、三维耦合水动力模型。模型在耦合界面上相互传递水动力参量,其中二维单元的流速垂向结构通过Van Rijn[30]的垂线流速分布公式得到。二维和三维水动力模型分别通过潮致环流算例和风生环流算例进行了验证,数值解与理论解吻合良好。潮流在斜坡地形上的传播实验表明将本文建立的二、三维耦合水动力模型有很好的可行性和实用性。综上,二、三维耦合水动力模型具有以下特点:(1)平面上采用非结构网格,能够较好地拟合复杂边界形状,同时可自由控制网格疏密,以达到提高工程区域计算精度的目的。(2)垂向上三维模型采用σ坐标变换,能更好地拟合地形起伏和水面波动。(3)二、三维耦合模型可以真实反映水流结构的垂向分布特征。(4)二、三维耦合模型较三维模型可以大幅提高计算速度,并且这一特性在大区域计算时更为突出,可以做到计算精度和计算效率的完美结合。
[1]李孟国,蔡东明,张征,等.海岸河口二维潮流可视化数值模型[J].海洋通报,2000,19(6):57-65. LIM G,CAID M,ZHANG Z,et al.A 2D tidal current visualization mathematical model for coastal and estuarine waters[J].Marine Science Bulletin,2000,19(6):57-65.
[2]李孟国,张华庆,陈汉宝,等.海岸河口多功能数学模型软件包TK-2D研究与应用[J].水道港口,2006,27(1):51-56. LIM G,ZHANG H Q,CHEN H B,et al.Study on multi-function mathematical model software package TK-2D and its application for coast and estuary[J].Journal of Waterway and Harbor,2006,27(1):51-56.
[3]李蓓,张征.二维波浪、潮流、泥沙淤积数学模型[J].水道港口,1993(3):36-42. LIB,ZHANG Z.A Two Dimensional Numerical Model of Wave-current-siltation[J].Journal of Waterway and Harbor,1993(3):36-42.
[4]张青玉,张廷芳.二维潮流的一个改进算法及其在长江口的应用[J].大连理工大学学报,1990,30(4):489-492. ZHANG Q Y,ZHANG T F.An improved algorithm for two dimensional tidal current and its application in Yangtze river estuary[J]. Journal of Dalian University of Technology,1990,30(4):489-492.
[5]谭维炎,胡四一.二维浅水流动的一种普适的高性能格式[J].水科学进展,1991,2(3):154-161. TANW Y,HU SY.A universal high-performance algorithm for two-dimensional unsteady shallow water flow computation[J].Advances in Water Science,1991,2(3):154-161.
[6]SONG L,ZHOU J,GUO J,et al.An unstructured finite volume model for dam-break floods with wet/dry fronts over complex topography[J].International Journal for Numerical Methods in Fluids,2011,67(8):960-980.
[7]窦振兴,杨连武,Ozer J.渤海三维潮流数值模拟[J].海洋学报,1993(5):1-15.
[8]李孟国.伶仃洋三维流场数值模拟[J].水动力学研究与进展,1996,11(3):342-351. LIM G.A numerical simulation of the three-dimensional flow field of Ling Ding Yang[J].Journal of Hydrodynamics,1996,11(3):342-351.
[9]Blumberg A F,Mellor G L.A description of a three-dimensional coastal ocean circulation model[J].Coastal and Estuarine Sciences, 1987,4:1-16.
[10]Chen C S,Liu H,Beardsley R C.An unstructured,finite-volume,three-dimensional,primitive equation ocean model:application to coastal ocean and estuaries[J].Journal of Atmospheric and Oceanic Technology,2003,20(1):159-186.
[11]Shchepetkin A F,Mcwilliams J C.The regional oceanic modeling system(ROMS):a split-explicit,free-surface,topography-following coordinate oceanic model[J].Ocean Modelling,2005,9(4):347-404.
[12]Miglio E,Perotto S,Saleri F.Model coupling techniques for free surface flow problems:Part I[J].Nonlinear Analysis:Theory,Methods &Applications,2005,63:1 885-1 896.
[13]YANG F L,ZHANG X F,TAN G M.One and two-dimensional coupled hydrodynamics model for dam break flow[J].Journal of Hydrodynamics,2007,19(6):769-775.
[14]Mahjoob A,Ghiassi R.Application of a coupling algorithm for the simulation of flow and pollution in open channels[J].World Applied Science Journal,2011,12(4):446-459.
[15]张大伟,李丹勋,陈稚聪,等.溃坝洪水的一维、二维耦合水动力模型及应用[J].水力发电学报,2010,20(2):149-154. ZHANG D W,LI D X,CHEN Z C,et al.Coupled one-and two-dimensional hydrodynamic models for levee-breach flood and its application[J].Journal of Hydroelectric Engineering,2010,20(2):149-154.
[16]王智勇,陈永灿,朱德军,等.一维-二维耦合的河湖系统整体水动力模型[J].水科学进展,2011(4):516-522.WANG ZY,CHEN Y C,ZHU D J.1D-2D coupled hydrodynamic simulation model of river-lake system[J].Advances in Water Science, 2011(4):516-522.
[17]王桂芬.二、三维潮流数学模型嵌套连接技术[J].交通与计算机,1988(3):39-40. WANGG F.Nest technology for two and three dimensional mathematical tidal model[J].Computer and Communications,1988(3):39-40.
[18]Namin M M,Falconer R A.An efficient coupled 2-DH and 3-D hydrodynamic model for river and coastal applications[C]//Phoon and Babovic.In Proceeding of the 6th International Conference on Hydroinformatics.Liong:World Scientific Publishing Company,2004.
[19]Zounemat K M,Sabbagh-Yazdi SR.Coupling of two-and three-dimensional hydrodynamic numerical models for simulating wind-induced currents in deep basins[J].Computers and Fluids,2010,39:994-1 011.
[20]Kilanehei F,Naeeni S T O,Namin M M.Coupling of 2DH-3D hydrodynamic numerical models for simulating flow around river hydraulic structures[J].World Applied Sciences Journal,2011,15(1):63-77.
[21]Rogers B D,Borthwick A G L,Taylor PH.Mathematical balancing of flux gradient and source terms prior to using Roe′s approximate Riemann solver[J].Journal of Computational Physics,2003,192(2):422-451.
[22]Liang Q H,Borthwick A G L.Adaptive quadtree simulation of shallow flows with wet-dry fronts over complex topography[J].Computers and Fluids,2009,38:221-234.
[23]Huang Y X,Zhang N C,Pei Y G.Well-balanced finite volume scheme for shallow water flooding and drying over arbitrary topography[J].Engineering Application of Computational Fluid Mechanics,2013,7(1):40-54.
[24]Toro E F.Shock-capturing methods for free-surface shallow flows[M].New York:Wiliey,2001.
[25]Song L X,Zhou J,Li Q,et al.An unstructured finite volume model for dam-break floods with wet/dry fronts over complex topography[J].Internal Journal for Numerical Methods in Fluids,2010,67(8):960-980.
[26]Anderson JD,Degroote J,Degrez G,et al.Computational Fluid Dynamics:Third Edition[M].Berlin:Springer,2009.
[27]Anderson W K,Bonhaus D L.An Implicit Upwind Algorithm for Commutating Turbulent Flows on Unstructured Grids[J].Computers Fluids,1994,23(1):1-21.
[28]Yang H Q,Przekwas A J.A comparative study of advanced shock capturing schemes applied to Burger′s equation[J].Journal of Computational Physics,1992,102:139-159.
[29]Umlauf L,Burchard H,Bolding K.General Ocean Turbulence Model.Sourcecode and test case documentation:Ver.4.0[M]. Warnemünde,Germany:Baltic Sea Research Institute Warnemünde,2005.
[30]Van Rijn L C.Principles of sediment transport in rivers,estuaries and coastal seas[M].Amsterdam,the Netherlands:Aqua Publications, 1993.
[31]Ippen A T.Estuary and Coastline Hydrodynamics[M].New York:McGraw Hill,1966.
[32]Koutitas C,O′Connor B.Modeling three-dimensional wind-induced flows[J].Journal of the Hydraulics Division,1980,106(11):1 843-1 865.
Research on a coupled 2D-3D hydrodynamic model I:model establishment
HUANG Yu-xin,ZHANG Ning-chuan
(State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology, Dalian 116024,China)
The numerical method for 2D and 3D hydrodynamic model was outlined.In practical studies,2D models are broadly employed to simulate the free surface flows.However,3D models are suitable for those cases that flow characteristics have significant variation in depth.A coupled 2D-3D hydrodynamic model was established based on their respective advantages.Then two well established benchmark test cases were carried out to verify the accuracy and reliability of 2D and 3D model,respectively.Finally,a comparison work was launched between the coupled system and 3D model,with the results showed good precision and considerable efficiency of the proposed coupled model.
coupled model;2D hydrodynamic model;3D hydrodynamic model;unstructured grid;finite volume method
TV 142;O 242.1
A
1005-8443(2013)04-0304-07
2013-01-28;
2013-02-25
创新研究群体科学基金(50921001)
黄玉新(1985-),男,安徽省宣城市人,博士研究生,主要从事海洋水动学方面研究。
Biography:HUANG Yu-xin(1985-),male,doctor student.
