强弯渠道三维水流数值模拟
2013-06-28艾丛芳
邢 岩,艾丛芳,金 生
(大连理工大学水利工程学院,大连116024)
强弯渠道三维水流数值模拟
邢 岩,艾丛芳,金 生
(大连理工大学水利工程学院,大连116024)
文章采用半隐有限体积方法建立求解渠道三维流动的数值模型,分别采用标准κ-ε和低雷诺数κ-w紊流封闭模型模拟定床条件下193°强弯渠道的流动特性。变量交错定义在水平非结构网格上,通过求解自由水位控制方程计算自由表面。计算值与试验测量值的对比,表明模型可用来模拟强弯渠道的三维流动,尤其对于渠道横向二次流运动,为进一步研究弯曲渠道的动床水力特性创造有力条件。
强弯渠道;紊流模型;二次流
蜿蜒曲折是天然河道的常态。行进在弯曲河道中的水流受床面和岸壁的限制,其水流运动特性与顺直河道不同,尤其对于强弯河道,曲折的岸线变化以及复杂的地形特征使其中的水流具有明显的三维特性(图1)。弯曲渠道沿流向方向的速度在河床处为0,而在自由水面或自由水面附近达到最大,这样就导致弯道离心力沿水深的差异,不同大小的离心力推动水流辐射状向外岸流动从而使弯道外岸水面形成超高,在弯道内外岸压力梯度差和离心力的共同作用下,靠近河床处的水流就会流向内岸以维持平衡,在河道断面上就形成了横向环流(即二次流),其与主流向流动的结合迫使流速分布做出调整,形成流态十分复杂的螺旋流。研究弯曲渠道的水流运动规律,尤其是二次流运动,对进一步研究渠道地形的冲淤乃至天然河道的形成和发展均具有重要的意义。
自1876年J.Thompson在试验中发现弯道水流同时存在着纵向和横向流动以来,很多学者致力于对该问题的研究,并取得了不少的研究成果。20世纪50年代罗索夫斯基[1]曾系统地研究了弯道水流的运动规律,波达波夫[2],张红武[3],王平义[4]和刘焕芳[5]等人从试验和理论分析上做了更进一步地研究。分别导出了水面横比降和环流流速沿垂向分布的公式。近年来,随着量测技术和数值模拟能力的发展进步,Blanckaert[6-9]针对弯曲渠道的流动和紊动特征做了大量试验与相关的模拟工作,Ruther[10],Khosronejad[11],Zeng[12-14]等人分别用各自不同的模型模拟弯道水流的流动,并取得了良好的模拟效果。本文建立非结构有限体积的方法求解三维水流运动的数值模型,分别采用标准κ-ε紊流模型和低雷诺数κ-w紊流模型模拟193°强弯渠道的水流特性,通过对弯曲渠道主要三维流动特性的结果展示和试验测量值对比,验证模型模拟复杂渠道三维流动的能力。
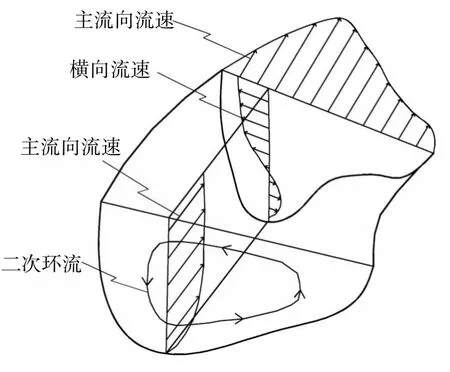
图1 弯曲渠段三维水流结构示意图Fig.1 Sketch of flow in channel bend
1 数值模型
1.1 水动力控制方程
对于不可压缩流体,对描述三维自由表面流动的控制方程Navier-Stokes方程做雷诺平均得到RANS方程,该方程反映流体流动质量守恒和动量守恒的物理规律,其在笛卡尔坐标系下可表示为连续性方程(质量守恒)

动量方程(动量守恒)
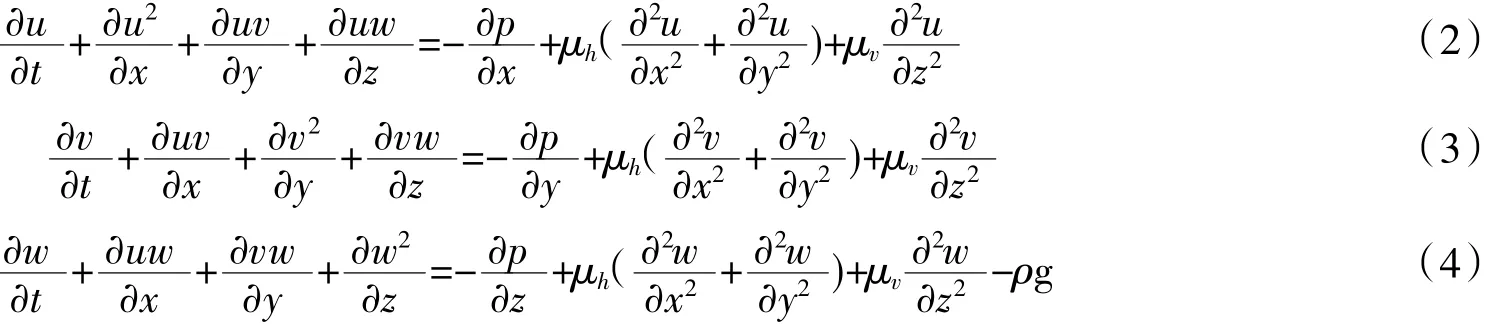
式中:u(x,y,z,t)、v(x,y,z,t)和w(x,y,z,t)分别为速度矢量沿x,y和z方向的分量;p(x,y,z,t)为压力和分别为水平和垂直方向的涡粘性系数;ρ为密度;g为重力加速度。
沿水深方向对连续性方程(1)积分,并运用自由表面和底部运动边界条件,则连续性方程成为水位方程

式中:η为自由水面水位;h为静水深。
把压力项p分解为静压项和非静压项,得到
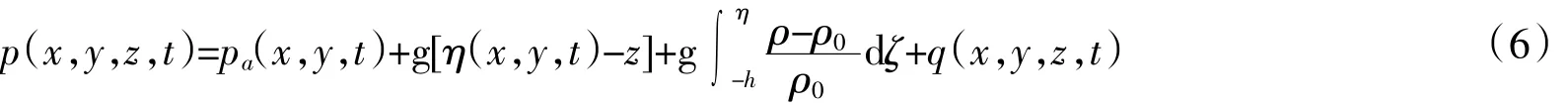
1.2 紊流模型
标准的k-ε紊流模型可表示为
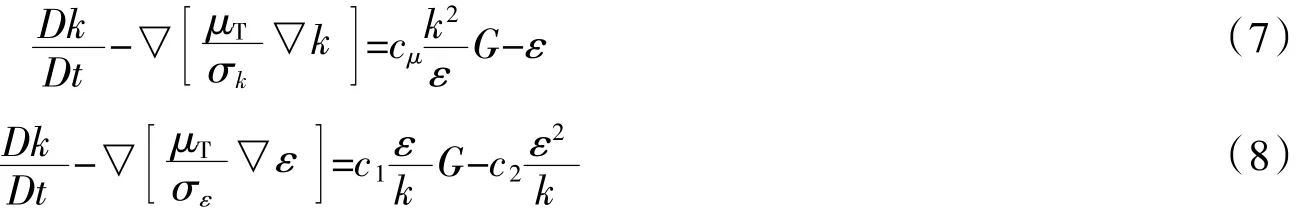
式中:cμ=0.09,c1=1.44,c2=1.92,σk=1.00,σε=1.30,G为湍动能产生项。
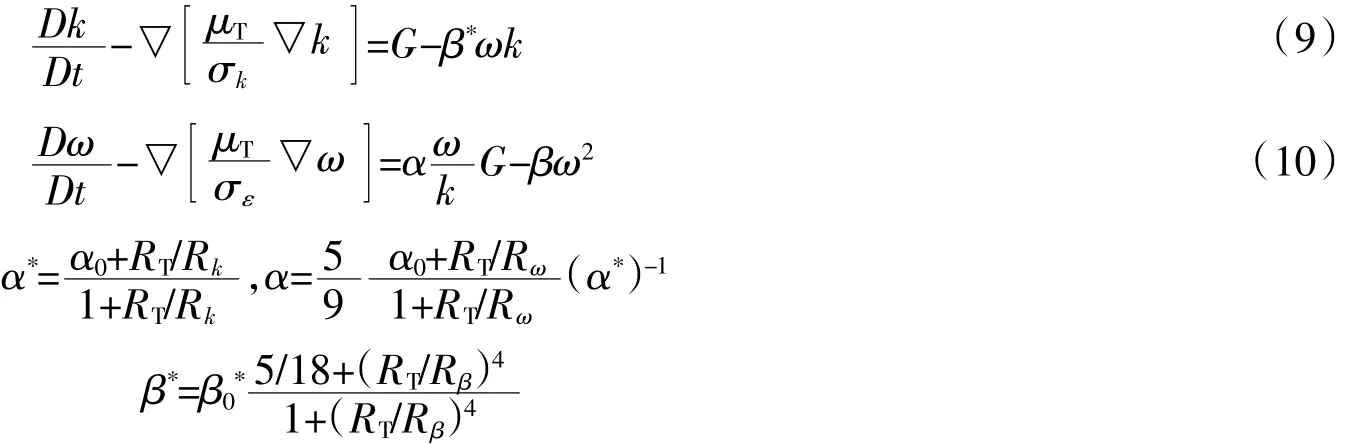
1.3 边界条件
底床边界条件可写成


式中:κ为von Karman常数,κ=0.41;Δz为底层垂向网格厚度;z0为底床摩擦系数,其与底床粗糙程度有关。
1.4 计算步骤
数值求解方法共分为三步[15-16]。第一步,对控制方程沿水深积分得到半离散的方程;第二步,通过半隐有限体积方法求解上一步得到的半离散方程,首先忽略自由水面的隐式项,求解得到中间步的流速,其中水平对流项和扩散项采用Perot格式[17]离散,然后,采用半隐有限体积方法求解包含自由表面隐式项在内的自由水面方程得到新时刻的自由水面,最后,代入动量方程得到新时刻的水平速度和垂向速度。第三步,求解湍流封闭模型,计算涡粘系数。
2 193°弯曲渠道试验
将数值模型应用于193°弯曲渠道实验[9](Blanckaert,2002),该实验布置如图2所示,宽度B=1.3 m的193°矩形弯曲渠段在其上游入口和下游出口分别连接长9m和长5m的矩形直段,弯段中心线的曲率半径为Rc=1.7 m,渠道中心线总长为19.7 m,渠道除上游入口段存在i=0.22%的坡度之外其余部分均为平底,渠底泥沙颗粒直径范围是1.6~2.2mm,中值粒径=2mm。入口流量Q=0.089m3/s,平均水深H=0.159m,平均流速V=0.43 m/s,弗劳德数Fr=0.34。弯曲渠段曲率半径和宽度的比率Rc/B为1.3,接近于1,属强弯渠道,二次流效应明显。
采用声学多普勒流速剖面测量仪(ADVP)采集恒定状态下相应断面沿纵向和横向的流场数据。在弯段每隔30°选定一断面,在上游入口直段分别取距弯
段入口0.5 m和2.5 m断面,而在下游出B口直段,分别取距弯段出口0.5 m、1.5 m和2.5m断面,断面布置如图2所示。
模型模拟渠道定床条件下的水流特征,采用非结构化网格,模型模拟步长为0.02 s,直至渠道水流达到恒定状态,模型底摩擦系数取=0.80mm,模拟分别选取κ-ε和κ-w两种紊流模型,以检验不同紊流模型的模拟效果。
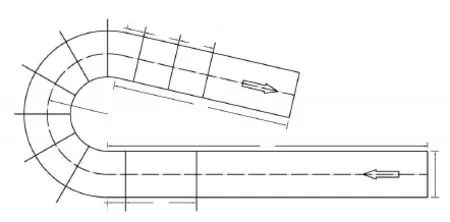
图2 193°弯曲渠段试验布置示意图Blanckaert(2002)Fig.2 Flume layout for the 193°channel bend experimentof Blanckaert(2002)
3 模拟结果与验证
为了验证模型模拟强弯渠道水流的能力,并对比不同紊流模型的模拟结果,分别从水位分布、表底层流场、水面横比降、纵向和横向垂线流速分布以及二次环流等方面展示模型的模拟结果。从总体上看,模拟体现了弯道水流的主要流动特征,与试验结果的对比也显示模型具有良好的模拟精度,不同紊流模型的模拟结果差别不大,其中κ-ε模型有相对满意的模拟结果。
3.1 平面流场
图3显示193°弯曲渠段水位分布等值线,从图中可以看出,弯曲渠段外岸水位明显高于内岸,除了临近弯段进出口的上下游直段水位受弯段影响,水位呈现外岸高内岸低的特征之外,其余直段内外岸水位均保持持平。受弯曲渠段离心力的作用,进入弯道的水流水位在外岸抬升,而内岸降低,其中内岸梯度较外岸偏大,内外岸水位差非常明显。在图5当中,显示渠段水面横比降试验测量值和计算值的无量纲化对比,从中可以定量地看出最大水面横比降发生位置和沿弯段水位变化过程。
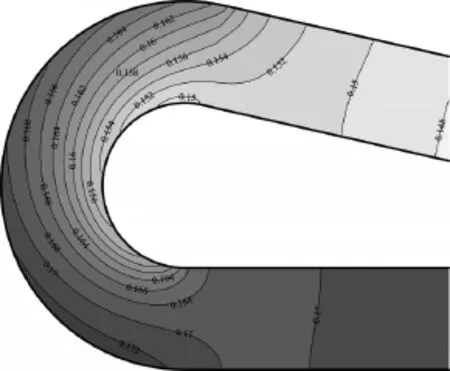
图3 弯曲渠段(局部)水位等值线图Fig.3 Water level contours of channel bend calculated by numericalmodel
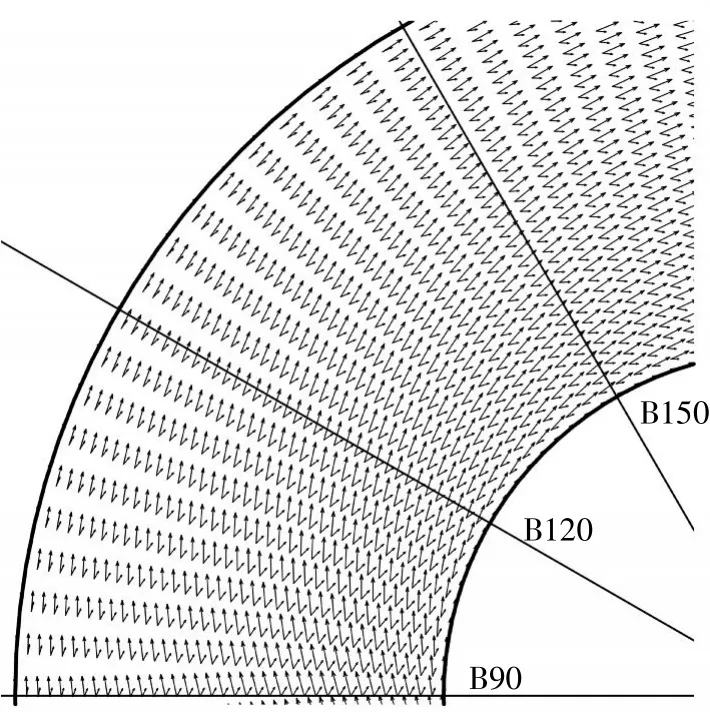
图4 弯曲渠段(90°~150°)表底层流速矢量场对比Fig.4 Surface and bottom velocity field of channel bend
图4显示弯曲渠段90°~150°部分表底层流速矢量场对比,从图中可以看出表底层流速大小和方向都有明显的差异,底层流速小且偏向内岸,而表层流速大且向外岸偏移,符合弯曲渠段内水体在内外岸压力差和离心力共同作用下表层水体流向外岸,底层水体流向内岸的流动形态以及物理特征描述。
3.2 水面横比降
图5为渠道沿程各断面水面横比降测量值与计算值对比。为便于比较,横纵坐标轴均进行了相应的无量纲化处理,其中hm表示断面上的平均水深,各断面上横向位置用η/H表示,其中-B/2<η<B/2。总体来看,除了30°弯段内岸附近模拟有较大偏差以及弯段进出口附近上下游直段有较小偏差外,模拟结果与试验测量值吻合良好,弯段外岸水位抬升和内岸水位降低幅度都有较准确地模拟,并且两种紊流模型模拟结果的差别不明显。上下游直段内外岸水位差别不大,而弯段内外岸水位差别明显,在90°弯段前后,内外岸水位差达到最大,也即水面横比降达到最大值,这与Blanckaert的试验观测值是一致的。
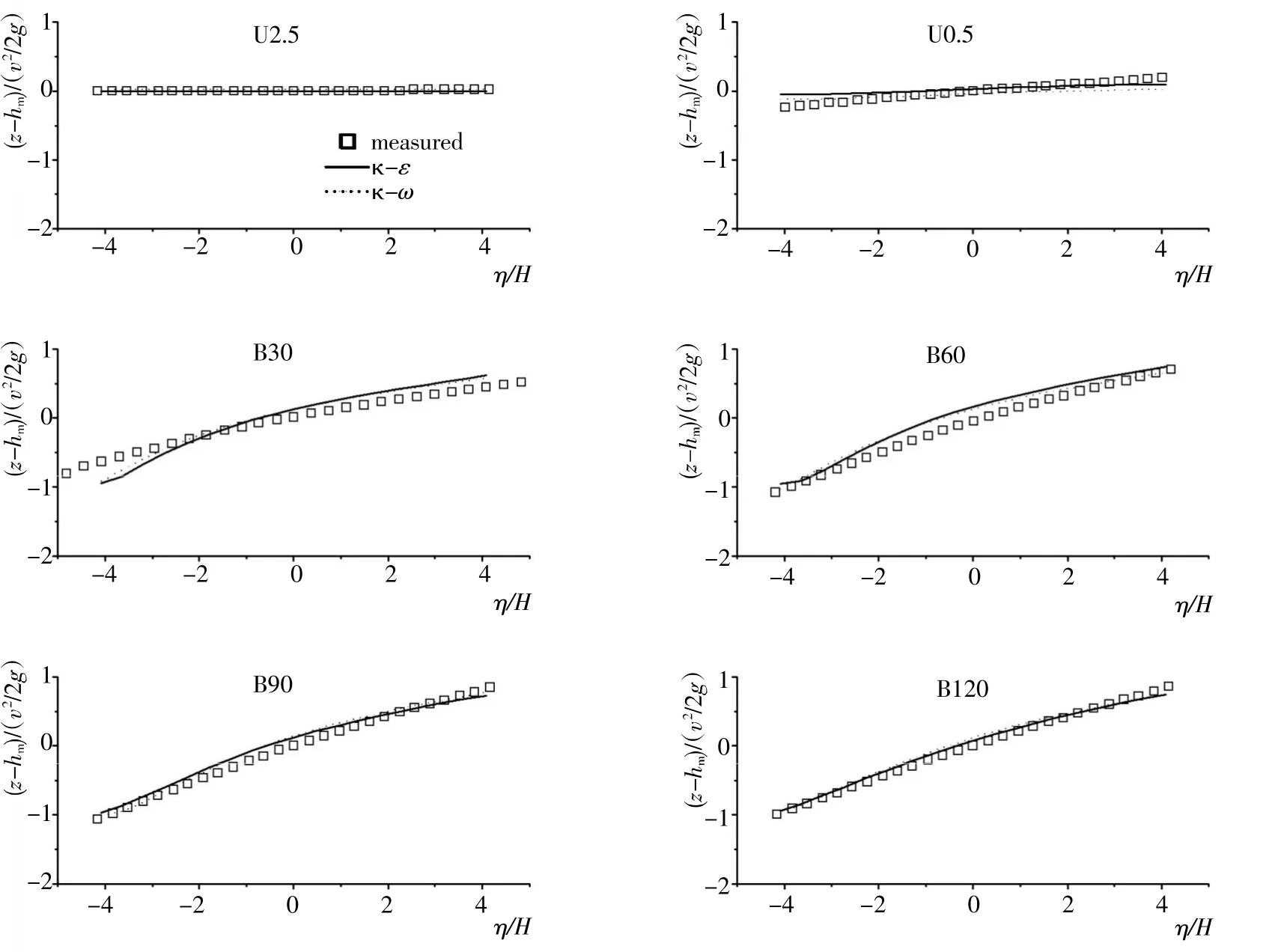
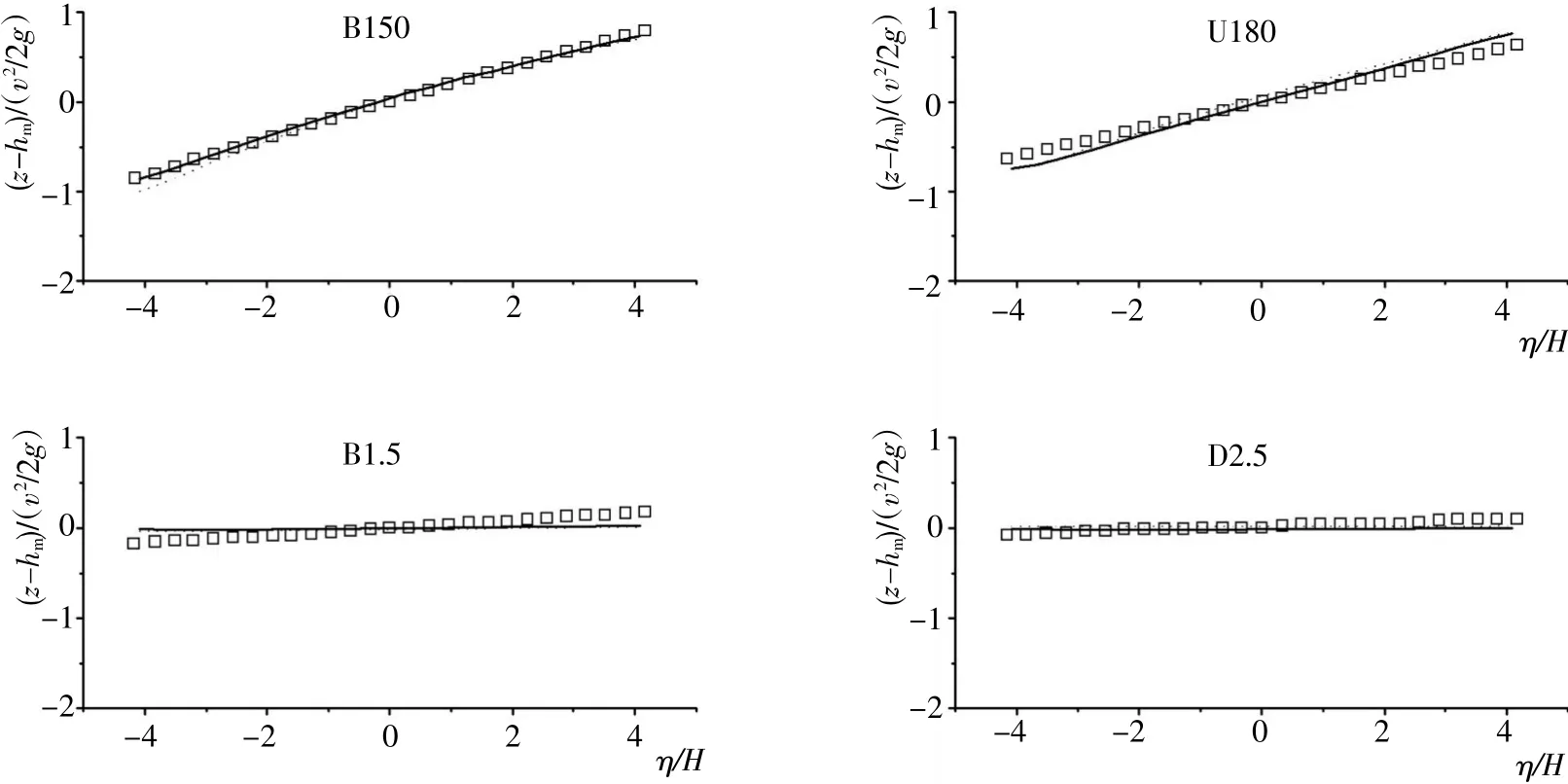
图5 沿程各断面水面横比降测量值(空心方框)和计算值(实线,虚线)对比Fig.5 Comparison between predicted and measured non-dimensional water level at various sections along the sharp curved channel bend
3.3 纵向和横向垂线流速分布
图6是渠道沿程各断面纵向垂线流速大小试验测量值与模拟结果对比。横纵坐标轴同样进行了无量纲化处理。在上游入口直段U0.5处,流动得以充分发展,流速分布呈典型的对数分布,从内岸到外岸流速大小和流速分布基本保持一致,表层流速大小都有较好模拟,但中间靠下位置模拟结果普遍比实测值偏小。在弯段B60处,水流受弯道弯曲效应的影响,内外岸流速大小和分布均出现较为明显的变化,表现为靠近外岸流速变小且分布沿水深变得平整,而内岸附近流速变大,流速分布从表层到底层保持单调,模拟结果与实测值吻合良好。在弯段B120处,外岸流速增加,内岸流速减小,靠近内岸流速分布不再保持单调,流速最大值出现在中间偏下位置,表层流速明显变小,两种紊流模型都模拟出表层流速变小的趋势,其中κ-ε紊流模型对表层流速减小的模拟更为准确。在弯段B180处,内岸流速减小,而外岸流速持续增加,内外岸流速差别不大,流速分布基本与B120保持一致,外岸表层流速明显变小,模拟结果有偏差。在下游直段D0.5处,内外岸流速变化明显,内岸流速持续减小,外岸流速明显增大,内外岸流速差别明显,内岸附近表层流速减小模拟有偏差,但κ-ε紊流模型依然比κ-ω准确。随着水流的持续前进,水流受弯道的弯曲效应逐渐减弱,内外岸流速大小和流速分布的差异越来越小,直至弯曲效应完全消失,内外岸再次恢复对称分布。
垂线流速分布的变化,譬如外岸分布平整化以及内岸最大流速值从表层往底层下移,均是因为二次流强度并不是随着渠道弯曲程度的增大而持续增强,其对流速分布自身的调整通过影响表底层离心力的变化进而限制二次流强度的不断增强[18]。
总体来看,受弯道弯曲效应变化的影响,渠道主流在进入弯道之后,呈现出从内岸向外岸逐渐移动的过程。当水流进入弯段,受弯道弯曲效应的作用内外岸流速不再对称分布,最大流速发生在靠近内岸一侧,也即主流靠近内岸一侧,随着水流的不断前进,弯道弯曲效应的变化,从弯段B120到B180,最大流速逐渐移动至渠道中心线位置,继而主流继续向外岸一侧移动,直至弯道出口附近,主流在靠近外岸一侧稳定下来,但最大流速在下游出口直段一定距离内依然持续增长。
图7是渠道沿程各断面横向垂线流速大小试验测量值与模拟结果对比。横向流速明显小于主流向流速,但其对横向输沙和底床冲淤有重要影响。横向流速分布表层流速为正指向外岸,而底层流速为负指向内岸,在断面上形成一个封闭的环流,即二次流。靠近底床附近的流速梯度最大,最大负向流速发生在近底床处,最大正向流速通常发生在表层附近。弯段B60处,靠近外岸表层存在负向流速,模拟结果与实测值有较大偏差,因为在该断面外岸近表层处,存在与二次环流逆向的外岸环流,该环流对稳定堤岸有积极意义,可能是因为模型所采用的κ-ε和κ-ω模型均为线性紊流模型,对模拟各向异性的涡流存在不足[12]。弯段B120处,流速分布和大小变化均不明显,从内岸到渠道轴线附近,与弯段B60处一样,底层负向流速模拟值比实测值稍小,并且在轴线位置表层流速也明显偏小。从弯段B180到下游直段D0.5,随着弯道弯曲效应的减弱,整个断面流速明显减小,模拟结果与测量值吻合良好。
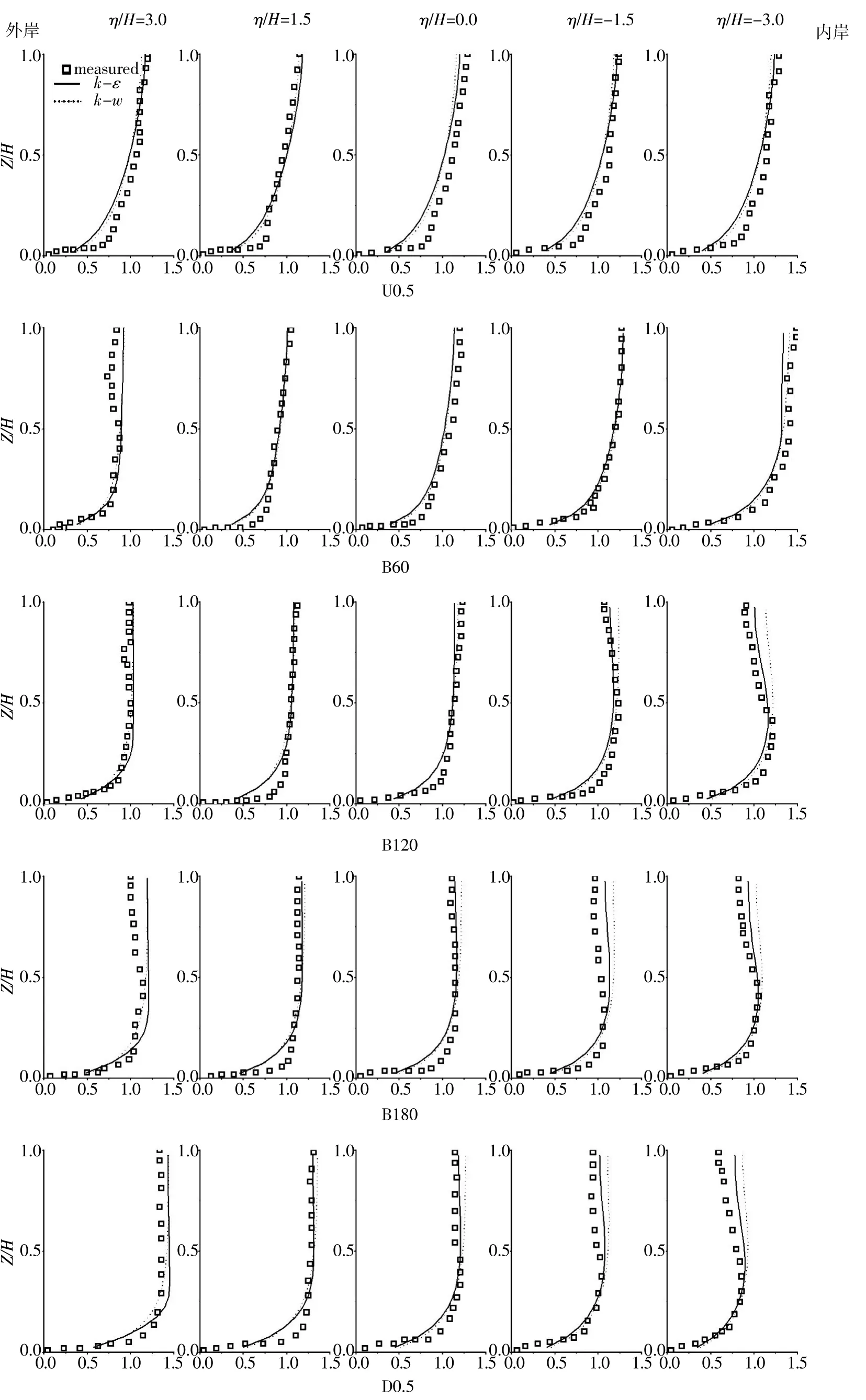
图6 沿程各断面纵向流速沿水深大小对比Fig.6 Comparison between predicted and measured longitudinal velocity profiles in several cross sections along the channel bend
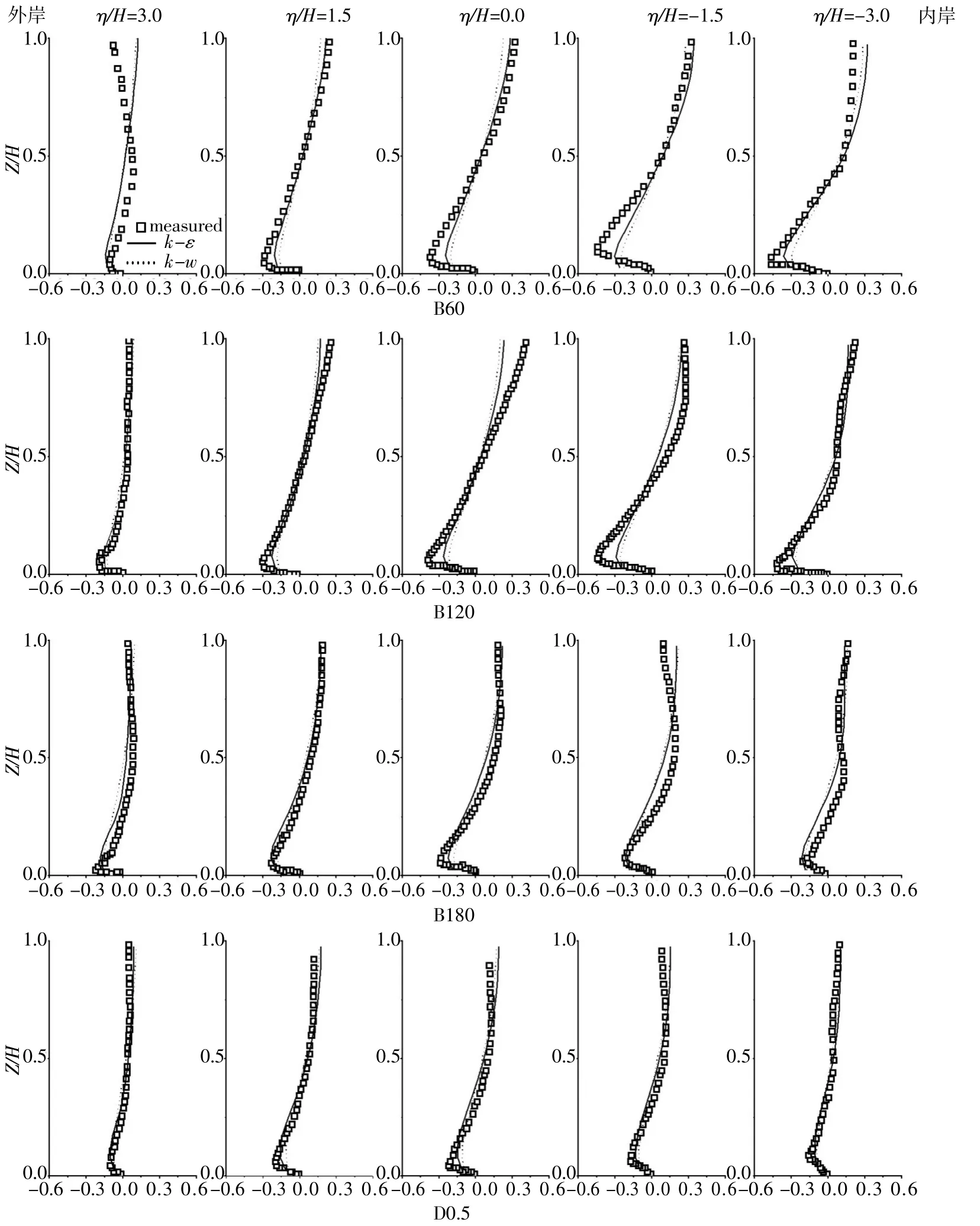
图7 沿程各断面横向流速沿水深大小对比Fig.7 Comparison between predicted and measured transverse velocity profiles in several cross sections along the channel bend
3.4 横向环流
图8是弯段B60,B120和B180横向二次环流和流线分布结果。从图中可以清楚地看出内外岸水位的差异,表层流场流向外岸,而底层流场流向内岸,在内外岸处由于受到岸壁的限制,在外岸表层水体向下流动,而在内岸底层水体向上流动,因此,在横向上构成了一个完整的涡流,该涡流与主流向流速的结合,使弯道内流速重新得到调整,形成复杂的三维螺旋流。从图8左侧(a,b和c)的流速矢量大小变化可以看出二次流强度逐渐减弱。
图8右侧(d,e和f)分别为相应断面环流场的流线分布,从中可以看出整个横向环流的流动特征,在弯段B60处,涡流中心的位置偏向内岸,弯段B120处,涡流中心移至弯道轴线附近,而在弯段B180处,涡流中心偏向外岸。
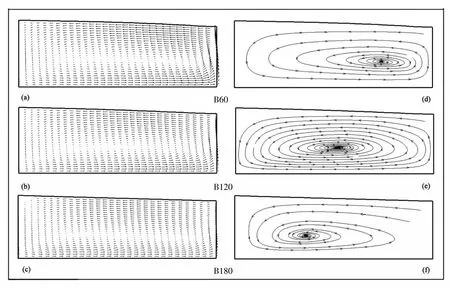
图8 弯段B60,B120和B180断面横向二次环流与流线分布(模型)Fig.8 Distributions of the transverse secondary circulation and 2D stream line patterns in several cross sections along the channel bend
4 结论
本文建立渠道三维流动的数值模型,分别采用标准κ-ε和低雷诺数κ-w紊流封闭模型模拟定床条件下193°强弯渠道的流动特性。通过水面横比降、纵向和横向沿水深流速分布3个方面试验测量结果与数值结果的对比,以及弯段水位分布等值线、表底层流速矢量场分布和横向二次环流的展示,得出的主要结论如下:
(1)该模型能用于模拟弯曲渠道的三维流动,对于曲率半径和宽度的比率接近于1的强弯渠道能保证较高的模拟精度。
(2)在193°强弯渠道模拟当中,κ-ε紊流模型的二次流效应要略强于κ-w紊流模型,并且其对主流向流速的模拟也优于κ-w模型。
(3)弯曲渠道中二次流效应的准确模拟,对进一步研究弯曲渠道横向泥沙输移,渠道冲淤具有积极意义。
[1]罗索夫斯基.弯道上横向环流及其水面形状的关系,弯道上纵向流速的分布[C]//水科院.河床演变论文集.北京:科学出版社,1965.
[2]波达波夫.波达波夫选集:第二卷[M].北京:水利电力出版社,1958:37-41.
[3]张红武,吕昕.弯道水力学[M].北京:水利电力出版社,1993.
[4]王平义,蔡金德,方铎,等.弯曲河道纵向垂线平均流速平面分布的研究[J].水动力学研究与进展,1994,9(3):267-275. WANG P Y,CAI JD,FANG D,et al.A study on the distribution of the depth-averaged longitudinal velocity in channel bends[J].Journal of Hydrodynamics,1994,9(3):267-275.
[5]刘焕芳.弯道自由水面形状的研究[J].水利学报,1990(4):46-50. LIU H F.A study on the shape of free-surface in channel bend[J].Journal of Hydraulic Engineering,1990(4):46-50.
[6]Blanckaert K.Flow and turbulence in sharp open-channel bends[D].Switzerland:Ecole Polytechnique Federale Lausanne,2002.
[7]Blanckaert K,Vriend H JDe.Turbulence structure in sharp open-channel bends[J].Journal of Fluid Mechanics,2004,536:27-48.
[8]Blanckaert K,Vriend H JDe.Turbulence characteristics in sharp open-channel bends[J].Physics of Fluids,2005,17(055102): 1-15.
[9]Blanckaert K,Vriend H JDe.Secondary flow in sharp open-channel bends[J].Journal of Fluid Mechanics,2004,498:353-380.
[10]Ruther N,Olsen N R.3D modeling of sediment transport in a narrow 90°channel bend[J].Journal of Hydraulic Engineering,2005,131(10):917-920.
[11]Khosronejad A,Rennie C,Neyshabouri S,et al.3D numerical modeling of flow and sediment transport in laboratory channel bends[J].Journal of Hydraulic Engineering,2007,133(10):1 123-1 134.
[12]Zeng J.Fully 3D non-hydrostatic model to compute flow,sediment transport and bed morphology changes for alluvial open channel bends[D].Iowa City:The Univ.of Iowa,2006.
[13]Zeng J,Constantinescu G,Weber L.A 3D non-hydrostatic model to predict flow and sediment transport in loose-bed channel bends[J].Journal of Hydraulic Research,2008,46(3):356-372.
[14]Zeng J,Constantinecu G,Blanckaert K,et al.Flow and bathymetry in sharp open-channel bends:Experiments and predictions[J].Water Resources Research,2008,44(W09401):1-22.
[15]Ai C F,Jin S,Lv B.A new fully non-hydrostatic 3D free surface flow model for water wave motions[J].International Journal for Numerical Methods in Fluids,2010,66(11):1 354-1 370.
[16]Xing Y,Ai C F,JS.A three-dimensional hydrodynamic and salinity transport model of estuarine circulation with an application to a macrotidal estuary[J].Applied Ocean Research,2013,39:53-71.
[17]Ai C F,Jin S.Non-hydrostatic finite volume model for non-linear waves interacting with structures[J].Computers&Fluids,2010,39(10):2 090-2 100.
[18]Blanckaert K,GrafW H.Momentum transport in sharp open channel bends[J].Journal of Hydraulic Engineering,2001,130:186-198.
上海将成长江航运信息枢纽
本刊从2013年7月20日召开的“2013长江及长三角航运信息化专网应用和产业发展座谈会”上获悉,一个覆盖长江“黄金水道”的航运综合信息服务平台将在上海临港软件园投入建设,未来上海将成为长江航运发展的信息枢纽。服务平台由一条宽带无线通信专网组成,长江沿线的各大港口、各航运企业的信息将能实现共享,物流客户可以实时查询货物的运输状态。(殷缶,梅深)
广西6口岸列入新开或扩大开放计划
本刊从广西自治区口岸办获悉,根据国家口岸管理办公室关于2013年度口岸开放审理计划文件精神,广西共有6个口岸列入新开或扩大开放计划。2013年我国有36个口岸列入新开或扩大开放计划,其中,水运口岸14个,含新开2个、扩大开放12个;防城、梧州、水口、东兴等口岸被列入扩大开放计划。(殷缶,梅深)
Three-dimensional modeling of flow in a sharp open-channel bend
XING Yan,AICong-fang,JIN Sheng
(School of Hydraulic Engineering,Dalian University of Technology,Dalian 116024,China)
A three-dimensional semi-implicit finite volume numerical model was developed and applied to solve flow characteristics of 193°open channel bend with flat bed based on the standard k-εand low Reynolds version k-w turbulence models.The model employs staggered definition on unstructured grid and obtains the free-surface water level by solving free-surface equation.After a series of comparisons between the observed data and calculated results,it indicates that the model can be used to calculate the 3D flows of sharp channel bend, especially for secondary flows.Furthermore,it creates favorable conditions for the next step study for flow and sediment transport of channel bend with movable bed.
sharp channel bend;turbulence model;secondary flow
TV 143+.1;O 242.1
A
1005-8443(2013)04-0335-09
2012-11-09;
2012-12-12
邢岩(1985-),男,河南省南阳人,博士研究生,主要从事水动力数值模拟。
Biography:XING Yan(1985-),male,doctor student.
