论平面空间的自然代数结构*

卢一兵，王应德，张海涛

(长沙大学电子与通信工程系，湖南长沙410003)

1 几何平面结构与复数代数结构的对应关系

众所周知，通过建立一个横轴为实轴，纵轴为虚轴的直角坐标系，可以建立起复数数系与几何平面之间的对应关系.然而，在这种对应关系中，不难发现，复数中与虚数相对应矢量和复数中与实数相对应的矢量，此两者总是相互垂直的.这是为什么呢?这种垂直关系是人为规定的，还是复数数系所固有的?对于这一问题，本文研究发现，在复数与平面相互应对应关系中，虚数矢量与实数矢量相互垂直的几何特性，并非是人为规定，而是由复数的数系结构所固有.

要想弄清复数系中虚数与实数存在着固有的几何垂直关系，我们首先就必须复数系中引入一种全新的复数运算，这种新的复数运算可称为复数的内积运算.

下面给出复数系中，任意两复数的内积运算定义:

设 za与 zb为任意复数为的共轭复数为 zb的共轭复数，“*”为任意两复数的内积运算符号.

定义任意两个复数za与zb的内积运算“* ”为:za*zb

由此定义，不难证明复数的内积运算“* ”，有下列基本性质:

(2)za*zb=zb*za，即复数的内积运算具有交换性.

(3)(za+zb)*zc=za*zc+zb*zc，即复数的内积运算对复数的加法运算具有分配性.

(5)z*z≥0，等号当且仅当z=0时成立.

按上述方式定义的复数运算“* ”，由线性空间理论知，应为一个内积运算，所以，可把按上述方式定义的复数运算称为复数的内积运算.

显然，复数系中定义的内积运算“*”与线性空间中的内积运算，在其体系的运算结构上还是有所区别的.

因为，在线性空间的理论中，对任意三个线性元素间，进行内积运算是没有意义的.而在复数系中，任意三个复数间，则是可进行内积运算的.且有下列运算特性:

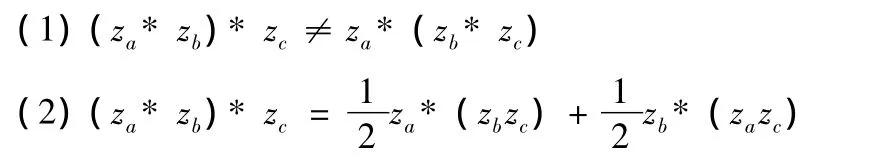
由于在复数系中，引入了内积运算，由线性空间的理论，建立起任一复数的长度或是任意两复数间夹角的概念.

在一个完备的几何结构中，除了要有长度与角度的概念处，还有一个重要的几何概念面积.为了使复数代数结构能与平面几何结构建立起更为严格的对应关系，因此，就必须在复数域中，进一步地引入一个新的复数运算，即复数的外积运算.下面给出复数系中，任意两复数间的外积运算定义.

设 za与zb为任意复数为za的共轭复数为zb的共轭复数，“∧”为任意两复数的外积运算符号.

定义任意两个复数za与zb的外积运算“∧”为:za∧zb

由此不难证明复数的外积运算“∧”，有下列基本性质:

(2)za∧zb=－(zb∧za)，即复数的外积运算具有反交换性.

(3)(za+zb)∧zc=za∧zc+zb∧zc，或za∧(zb+zc)=za∧zb+za∧zc.即复数的外积运算对复数的加法运算具有分配性.

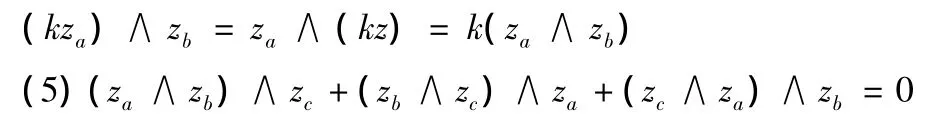
显然，按上述方式定义的复数外积运算“∧”，在复数域中还应是一个李代数.由于，在复数中引入了复数的外积运算，由线性空间理论知:

综上所述，平面几何理论结构，在数学理论的逻辑结构上，是与代数数系的体系结构相互对应的.过去人们之所之没有发现这种对应关系，本文认为，根本的原因在于，在以往的复数代数理论中，没有建立起与之相应的代数运算.只要在复数的代数理论中，引入复数的内积与外积运算，由线性空间理论知，代数理论中的“数”与几何理论中的“形”便可成为一个统一的整体.显然，这种能把代数的与几何的形统一的数学理论，要比笛卡尔的解析几何理论形式更为高级.

2 几何平面结构与其它二元代数结构的对应关系

我们所感兴趣的问题是，能够把数与形在结构上统一起来的代数数系，是否就一定只能是复数系中的数?

由现代代数理论知，这一问题的答案，显然是否定的.下面先给出一个不同于复数系的二元代数数系.

从群代数的理论来看，常用的复数系，是由一个四阶循环群与一个实数域结合构成的.这个四阶群的四个元素可记为(1，－1，i，－i).既然，四阶循环群与实数域结合能形成一个二维的复数代数.那么，用其它的可交换四阶群与一个实数域结合是否也能形成一个新的二维代数数系呢?对此问题，通过本课题的研究结果表明，完全可以形成一个新的不同已知复数数系的二维代数数系.

众所周知，在四阶可交换群中，除了四阶循环群外，还有一个四阶克莱因(Klein)群，如果把此群中的每个元素分别表为，(e1，e2，e3，e4)，则此克莱因(Klein)群关于乘法运算的运算表为:

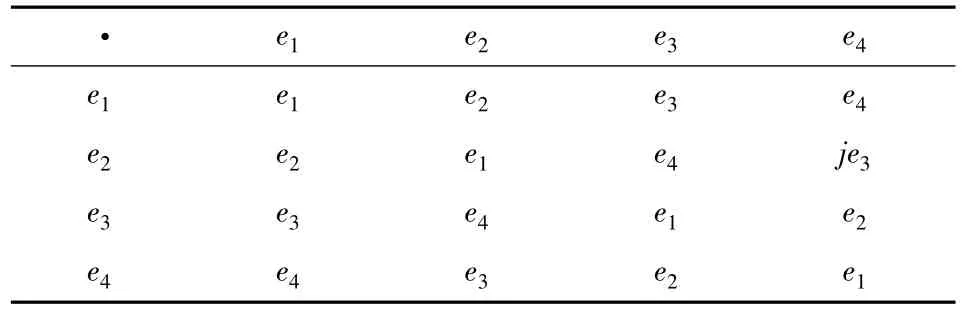
·e1 e2 e3 e4 e1 e1 e2 e3 e4 e2 e2 e1 e4 je3 e3 e3 e4 e1 e2 e4 e4 e3 e2 e1

在此群表中，如果把单位元e1记为数1，其余的三个元素 e2，e3，e4分别记为 － 1，j，－ j，则此群表则为如下形式

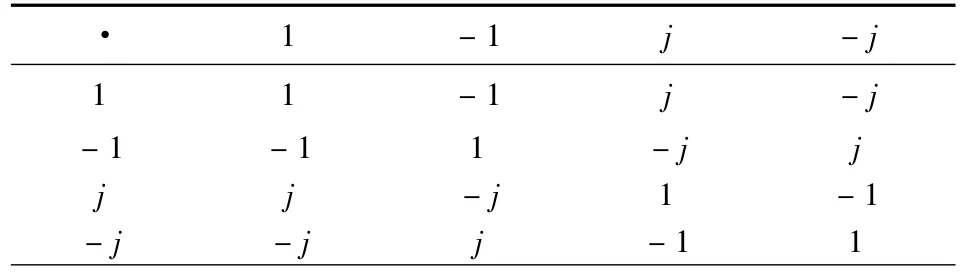
·1－1j －j－j－1 －1 1 －j j j j－j 1 －1－j －j j －1 1 1－1j 1

把此群表与四阶循环群(1，－1，i，－i)的运算表对比

·1－1i －i－i－1 －1 1 －i i i i－i －1 1－i －i i 1 －1 1 1－1i

显然两者是不同的.在四阶克莱因(Klein)群中，其单位元素e1，可视为一个实数单位，记为数1，而非单位元的元素e3记为j后，由于j不是实数且j2=1，仿照复数数对i2=－1中i的称法，则可视为一个广义的“虚数”单位.

如果，按照四阶循环群(1，－1，i，－i)与实数域的结合方法，把四阶克莱因(Klein)群与实数结合起来，则不难构建一个不同于传统意义的新的二元“复数”数系.

在此新的二维代数系中，任一个数都可表为z=x+yj，且有

如果，z1=x1+y1j，z2=x2+y2j，则

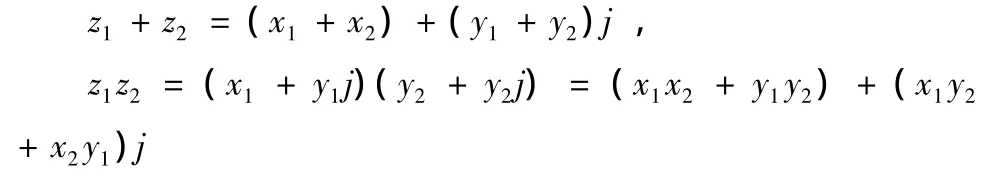
由于，此数系中的数是以克莱因(Klein)群为基础构造而成的，故本文把这种新的数，则命名为“克莱因数”.

克莱因数的代数表示与复数的代数表示相近，有虚实两个部分，且同样可有共轭的概念.在克莱因数系中，设za与zb为任意两数为za的共轭数为zb的共轭数，则数za与zb和数为za，有如下表示形式:

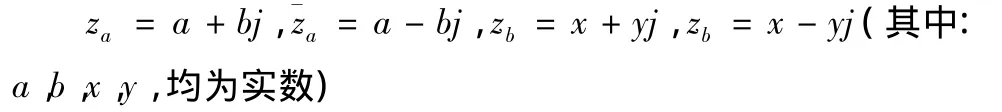
在克莱因数系中，任意两数za与zb的乘法运算为，

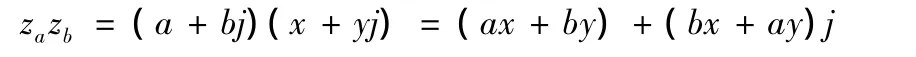
注意到，在复数中，任意两复数za与zb的乘法运算，则是

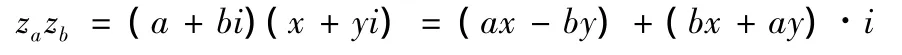
显然，克莱因数的乘法运算结构与复数系乘法运算结构是不同构的.由克莱因数系的代数结构，我们不难证明，克莱因数系的代数结构是一个具有零元的可交换环.而我们所熟知的复数系，其代数结构则是一个域.因此，新的二元克莱因数系与熟知的复数系在代数结构上是不同构的.

下面探讨克莱因数系的代数结构与平面几结构的相互对应关系.要想弄清，克莱因数系与平面几何结构的对应关系，首先在克莱因数系中，引入相应的内积与外积运算.

下面给出克莱因数系中，任意两数间的内积运算的定义

设 za与 zb为任意克莱因数为 za的共轭数为 zb的共轭数，“* ”为任意两克莱因数的内积运算符号

定义任意两个数za与zb的内积运算“*”为:za*zb

由此定义，不难证明克莱因数数的内积运算“* ”，有下列基本性质

(2)za*zb=zb*za，即复数的内积运算具有交换性.

(3)(za+zb)*zc=za*zc+zb*zc，即复数的内积运算对复数的加法运算具有分配性.

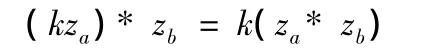
(5)z*z≥0，等号当且仅当z=0时成立.

由此可知，在克莱因数系中，当 k为实数时，必有k*(αj)=0，故实数k与虚数αj，总是相互垂直的.

由于，在克莱因数系中，引入了内积运算，故在克莱因数系中不难给出任一数的长度或任意两数夹角的定义.

任意两克莱因数间的夹角定义为:＜za，zb＞≡arc cos，特别地，当za*zb=0时，则克莱因数za与zb相互垂直.

为使克莱因数系中的数，能与几何理论更紧密结合起来，在克莱因数系中，同样可引入相应的外积运算.其定义形式与复数系中外积定义形式相同.

即定义任意两个克莱因数za与zb的外积运算“∧”为:

由此定义，不难证明克莱因数的外积运算“∧”，有下列基本性质

(1)za∧zb=，即任意两非零克莱因数za与zb的外积必为一虚数.

(2)za∧zb=－(zb∧za)，即克莱因数的外积运算具有反交换性.

(3)(za+zb)∧ zc=za∧ zc+zb∧ zc，或 za∧ (zb+zc)=za∧zb+za∧zc，即克莱因数的外积运算对复数的加法运算具有分配性.

综上所述，我们不难发现，只要在克莱因数系中，引入两个新的内积与外积运算，那么，平面几何的理论结构体系，同样可以在克莱因数系中重新构建起来.因此，几何平面结构与广义的复代数结构，同样存在着相互对应的关系.由此可知，几何平面结构与代数结构的相互对应并非是一一对应关系，而是一对多的关系.

通过对平面的自然代数结构这一问题的研究，本文发现，虽然，二元代数数系的种类多种多样，但是，无论是何种形式的二元代数数系，只要在其中引入与之相应的内积与外积的代数运算，那么，在此二元代数数系中，必定能有一个不依赖于二元数系具体形式的二维空间结构与之相联系.

在数学的理论体系中，如果能用代数结构与几何结构相对应的思想，把n元代数的数与n维几何的形相互统一起来，使之构成一个统一的整体.这种对应思想的实质，就是把某个有限群与一个域结合起来使之成为一个新的代数体系，而在此代数体系中，通过借助其固有的代数运算，使几何结构与代数结构成为一个统一整体.在这种统一体中，群，环，域，不仅是一种代数结构，同时也是一种几何结构.因为，此时数系中的代数元素相加，就是几何的有向线段相加，而群元素间的代数运算，也就是几何线段图形的几何运算.所以，数学代数理论中所谓的“抽象代数”实质上也就是一种“抽象的几何”理论.

长期以来，人们总想弄清，物理空间为什么只能是三维的?对此问题，虽然，在代数理论中，已经证明三维的复数域是不可能存在的.但这并等于否定不存在与三维空间结构相对应的代数数系.因为，我们现已找到能与三维空间结构相对的代数数系，并且发现，通过由此代数数系中所定义的内积与外积运算，确实能建立起数与形的相互统一.凡是对此有兴趣的学者不妨试试便知.

总之，通过本文的研究，所得到的结论是，在整个数学理论体系中，代数的数与几何的形是相互对应且自然统一的.构成代数理论体系的基本元素数量，与构成几何理论体系的基本元素矢量，在数学理论的逻辑结构中实是同一元素.在平面空间结构中是如此，在三维空间结构中同样也是如此.