基于改进灰色模型的电力系统负荷预测

赵金龙，陈晓宁，耿勇，朱瑞德

（解放军理工大学，南京 210007）

基于改进灰色模型的电力系统负荷预测

赵金龙，陈晓宁，耿勇，朱瑞德

（解放军理工大学，南京 210007）

传统的灰色预测模型因其所需历史数据少、计算快、对平稳地区的负荷预测有较高精度等优点，曾被广泛应用。但传统的灰色预测模型对于历史数据要求较高，最好为指数形式，并且在数据波动较大的情况下，其预测误差可能变得较大，不符合实际需要。为了减小预测误差，本文在传统灰色模型的基础上，首先对部分历史数据进行平滑处理，以确保其光滑性，同时对历史数据进行等维处理，不断的剔除旧数据，增加新数据，最后进行灰色循环残差修正，在原始数据和预测模型两个方面进行了修正，提高了电力负荷预测精度。

GM(1,1)模型 循环残差修正模型 等维处理 负荷预测 预测精度

0 引言

电力系统负荷预测是根据电力负荷、社会、经济、气象等历史数据，特别是气象和经济数据[2]，探索电力负荷历史数据变化规律对未来负荷的影响，寻求电力负荷与各种相关因素之间的内在联系，从而对未来的电力负荷进行科学的预测[3]。在电网规划中，电力负荷预测精度直接决定投资成本，早在1985年英国的一份研究报告表明:英国电力负荷预测的误差每增多一个百分点，每年的经济损失就达一千万英镑。因此，选择一种预测精度高的电力负荷预测办法至关重要。电力系统负荷预测的方法有很多，包括时间序列法、回归分析法、人工神经网络技术、专家系统和模糊逻辑系统等。中国学者邓聚龙教授于80年代创立的灰色系统理论，是一种研究少数据、贫信息不确定性问题的新方法。灰色预测模型法在建模时不需要计算统计特征量，从理论上讲，可以使用于任何非线性变化的负荷指标预测，但其也存在一定的局限性，当历史数据离散程度较大时，数据灰度较大预测精度会较差，其应用于电力系统中长期负荷预测中，仅仅是最近的几个预测数据精度较高，其它较远的数据只反映趋势值和规划值。为此，本文对灰色预测模型进行了改进，用以提高负荷预测精度，即采用对数据预处理和循环残差修正模型的办法，对电力系统进行短期和超短期负荷预测。

1 传统的灰色预测模型

灰色预测模型（Gray Model，GM）是将一切随机变化量看作是在一定范围内变化的灰色量，常用累加生成、累减生成、均值生成、级比生成等方法将杂乱无章的原始数据整理成规律性较强的生成数据列。用灰色模型（GM）的微分方程作为电力系统负荷的预测方法时，求解微分方程的时间响应函数表达式即为所求的灰色预测模型，对模型的精度和可信度进行校验并修正后即可据此模型预测未来的负荷。

一般建模是用数据列建立差分方程，而灰色模型是将历史数据列生成后，建立微分方程模型。GM(1,1)模型是最常用的一种灰色模型，它是由一个只包含单变量的一阶微分方程构成的模型，是作为电力负荷预测的一种有效的模型，是GM(1,n)模型的特例，建立GM(1,1)模型只需要一个数列。

对随机序列

作一次累加生成序列，

其中，

由于序列[x(1)(k),k=1,2…]具有指数增长规律，而一阶微分方程的解正好是指数增长形式的解。因此，认为新生成的序列满足下面一阶线性微分方程模型：

式中参数a为发展系数，反映了x(1)和x(0)的发展态势；u为灰色作用量，是从背景值挖掘出来的数据，其确切内涵是灰色的。解微分方程可得a，u，x(1)和x(0)之间有如下关系：

上述方程组中，A为待定参数，Yn和B为已知量，用最小二乘法得到最小二乘近似解，解为：

将a，u代回原来的微分方程，可得方程的解为：

其中，k=0,1,2…,n。

根据此预测结果再进行累减还原，就可以得到原始数据序列的灰色预测模型：

其中，k=0,1,2…,n。

2 灰色预测模型的改进

传统的灰色预测模型存在一定的局限性，为了提高预测精度，可对灰色预测模型进行适当的修正。从GM（1,1）模型建模过程可以看出，其预测精度取决于a和u两个值，而影响a和u大小的原因主要有: 1）原始数据的离散程度; 2）背景值的选择; 3）初始值的选取。这三个原因直接影响模型的预测精度。

针对上述三个方面的原因，本文采用对原始数据序列的预处理和对预测模型修正的方法来改进灰色预测模型，以提高其预测精度。

2.1 数据预处理

负荷预测是在历史数据基础上对负荷未来状态的预测，因此，历史数据的好坏在很大程度上决定了预测的精度。在预测前，可大致观察历史数据，剔除偏离较大的异常数据，以此来确保准确度。

随着时间的推移，新的检测数据不断补充，由于新数据带入了新的扰动和驱动因素，使系统受到这些最新信息的影响而发生新的变化趋势，相应地，老数据的信息意义随着时间推移将不断降低。另外，预测时的运算量也越来越大，不便于计算机处理。因此，对GM（1,1）模型进行等维新息处理，即每增加一个新的信息，便将最老的一个信息去掉。这样等维新息模型可以不断地利用新数据来建立预测模型，以实现动态预测，从而提高了预测精度。

2.2 灰色循环残差修正模型

设用原始序列x(0)(i)建立的GM（1,1）模型可获得生成序列(0)(k)的预测值，定义残差序列，使用残差序列式加上预测序列式可得一组新序列公式为：

对序列y(0)(t)作一次累加生成得序列y(1)(t)，建立相应的GM预测模型：

微分方程中的a，u两参数同样可由最小二乘法求得，将参数a，u代入微分方程中，可求得函数为：

再作逆累加生成还原可得：

至此，即可得到一组GM(1,1)残差修正模型的预测序列。

图1为改进的灰色模型的负荷预测流程图。

2.3 误差计算

改进的负荷预测模型建立后，要检验其预测精度，首先计算残差序列：

及相对误差序列：

计算平均相对误差：

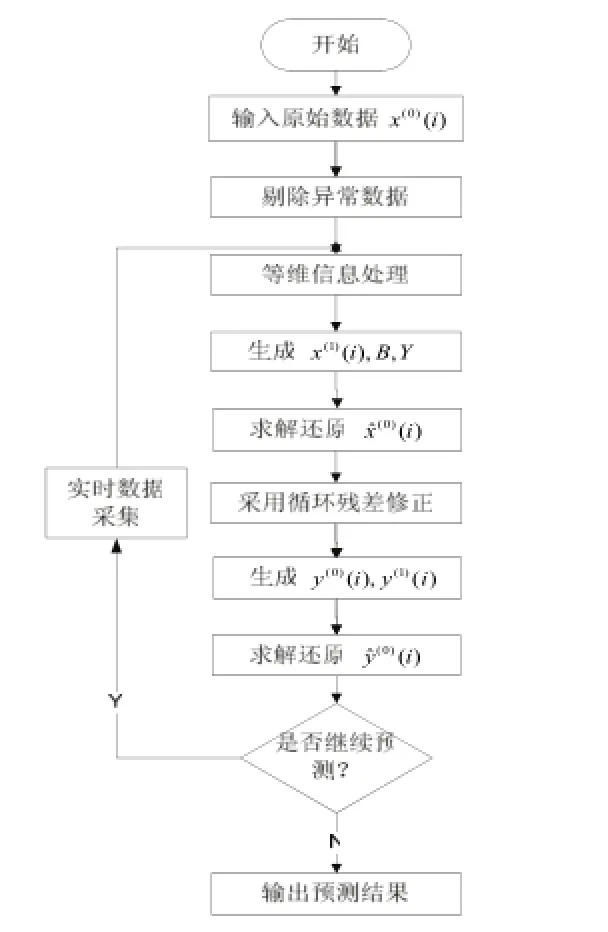
图1 改进的灰色模型预测流程图

3 实例计算

本文采用GM（1,1）模型和修正模型分别对某地区2005年3月份负荷进行预测和处理，通过误差对比来检验其预测精度和改进效果。图2为所选负荷实际值的曲线图。

通过观察可发现该地区2005年3月11号的数据，存在明显异常，不按照历史规律进行运行，剔除。在实际预测中，工作日的负荷变化与周末时的情况不同，存在一定的差异性，将工作日和周末分开预测，将有助于提高预测精度。此外，由于本文所做的改进模型并不针对于节假日负荷预测，所以只做工作日的预测。

3.1 实例1历史数据数目的影响

对于灰色模型而言，选取的历史数据的数目有一定的要求，不可以太多，也不可以太少，理论上一般选取3到7天的数据为基础进行预测。表1给出了不同历史数据数目下的预测结果，由表可以看出，以5天的历史数据为基础进行预测时，预测精度最高。

3.2 实例2预测模型修正前后某工作日每小时电力负荷预测精度对比

表2给出了灰色模型修正前后对某地区2005年3月17日全天24小时电力负荷的预测值及预测误差，其中第一行列出了需要对比的各项内容，并在最后一行给出了平均误差。图3为预测模型修正前后的负荷曲线图。根据上表及曲线图，可以看出，修正后的模型平均误差精度由-3.38%提高到-1.39%，修正后的预测数据光滑程度明显高于修正前，预测结果非常接近实际值。此外,我们还可以看出，修正前，0点到8点的负荷预测值偏差不大，预测精度较高，但在10点到19点之间，随着用电量的大量增加，预测值偏差较大。通常在一些负荷变化的转折点预测精度有所降低，这就需要精确的修正模型来修正不足。

4 结论

通过实例计算，可以看出，原始的灰色模型在预测中，误差较大，不能满足实际需求，只有多种方式的修正方法有机的结合才能使预测结果更加精确。本文所提出的循环修正模型证实了其有利于提高电力负荷预测的性能和精度，所选取得灰色模型对于历史数据需求量小，受天气、温度、湿度等影响较小，在短期负荷预测中，精确度较高。实验结果表明了预测方法的有效性和科学性，预测结果令人满意。

[1] 李小燕. 基于灰色理论的电力负荷预测[D]. 武汉：华中科技大学，2007.

[2] 余健明，燕飞，杨文宇等. 中长期电力负荷的变权灰色组合预测模型[J]. 电网技术, 2005, 29(17): 26-29.

[3] 王吉权. 地方电力系统负荷预测的研究[D]. 哈尔滨：东北农业大学, 2004.

Power System Load Forecasting Based on Improvement of Grey Model

Zhao Jinlong，Chen Xiaoning，Geng Yong，Zhu Ruide

(PLA University of Science&Technology，Nanjing 210007，Jiangsu, China)

The general gray model needs a fewer history data, calculates faster and makes high precision to load forecast of areas with stable load. So it is widely used. The general grey forecasting model demands higher quality of historical data, the best form is the index. It has the distinct deviation under the circumstances of considerable data fluctuations. This is against the actual condition. In order to reduce forecasting errors, Based on traditional gray model in this paper, historical data is smoothed to ensure smoothness, processes with equal dimension which continuously removes the old data and adds new data. We establish an RRGM(1,1) model and make a revise in the raw data and prediction model with high forecasting precision.

GM(1,1) model; RRGM(1,1) model; processing with equal dimension; load forecasting; forecast accuracy

TM715

A

1003-4862（2013）05-0031-04

2012-10-15

赵金龙（1989-），男，硕士研究生。研究方向：电力系统保护与控制。