中部地区技术创新能力实证研究

梁 艳

（安徽财贸职业学院基础部，安徽合肥230601）

中部地区技术创新能力实证研究

梁 艳

（安徽财贸职业学院基础部，安徽合肥230601）

采用理论分析和实证研究相结合的方法，运用面板数据通过建立随机效应变截距知识生产函数模型，对中部六省的技术创新能力进行比较分析，进而揭示中部地区各省技术创新能力的差异。

技术创新能力；面板数据；知识生产函数

1 模型的选择与建立

分析技术创新与区域创新的重要理论工具是知识生产函数，其基本假设是将技术创新过程的产出看做是研发资本或研发人员投入的函数，用柯布道格拉斯生产函数可以表示为：

其中，α为常数，β为研发产出对于创新过程中投入变化的弹性。对式（1）两端取自然对数，利用Eviews软件就可估计出常数α和弹性系数β。

杰菲认为新经济知识是技术创新最重要的产出，企业追求新经济知识并将其投入生产过程，技术创新的投入变量包括投入的研究经费和投入的人力资源。杰菲生产知识函数模型的一般形式：

其中，Q表示研发活动的强度；K表示投入的R＆D经费；L表示投入的科技人力资源；α、β分别为R＆D经费投入的弹性系数和科技人力资源投入的弹性系数；ε为随机误差项，i为观测单位。

随着经济社会发展的迅猛发展，技术创新作用越来越明显，制度改革一直在进行，制度创新对技术创新的影响日益突出，从而对经济社会发展的作用也渐渐凸显。所以有些学者在研究类似问题及选择解释变量时，也会考虑到制度因素。

借鉴以前学者的相关研究状况以及结合相关实际情况，本文确定的解释变量为人力资本和制度因素两个方面，被解释变量是研发活动的产出。最终建立的模型如下：

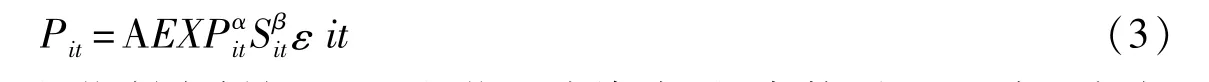
其中，P是指研究与开发活动的产出；S是指制度创新；EXP是指人力资本，是常数项；A可表示把投入的人力资本和制度创新转化成研发活动产出的能力，即产出效率，也即技术创新效率；ε是随机扰动项；i代表观测单位；t是指时间变量。

考虑到数据的易得性，我们用专利申请的授权数代表研发活动的产出，用R＆D人员全时当量代表人力资本，用市场化程度代表制度创新，为了用Eviews对模型（3）进行估计，需要转换为双对数模型，因为这样更加有利于对模型的系数进行估计，所以双对数线性知识生产模型为：

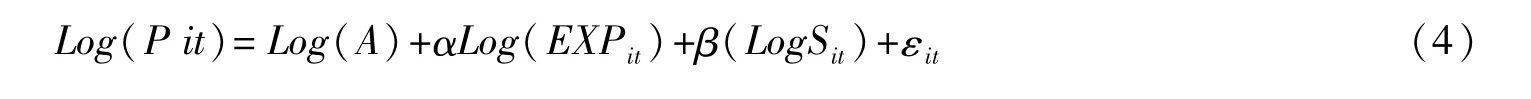
2 数据的选取及处理

本文的数据来源于2005—2012年《中国科技统计年鉴》和《中国统计年鉴》，中部六省的每个省的2005—2012年《统计年鉴》和《科技年鉴》。这些数据的时间跨度为2004—2011年，共8年，即每一个变量包含48个数据。

对于统计年鉴的一些数据，进行了适当的处理。其中制度创新S用投资的市场化指数表示，即非国有、集体投资占全社会固定资产总投资的比重。

3 实证分析与结果解释

对中部地区山西、安徽、江西、河南、湖北、湖南六个省2004—2011年处理后的面板数据，基于模型（4）利用统计软件Eviews6.0进行估计，比较中部六省的技术创新能力的大小。

本文通过似然比检验和Hausman检验对这三个模型进行取舍。

3.1 实证分析

3.1.1 对模型（4）建立混合效应模型

设混合效应模型为：yit＝α+βxit+εit，i＝1，2，3，…N，t＝1，2，3，…T。其中y为被解释变量，x为解释变量，β为系数，ε为随机误差项，α和β不随i，t变化，软件输出结果如表1所示：

表1 混合效应模型OLS估计结果

根据Eviews软件输出结果可知：在5%的显著性水平下，解释变量均显著，混合效应模型中修正的R2为0.8975，F统计量的值为206.7078。

3.1.2 对模型（4）建立固定效应模型

设固定效应模型为：yit＝αi+βxit+εit，i＝1，2，3，…，N，t＝1，2，3，…，T。其中αi对于每一个截面为固定常数，代表每个截面的差异。通过Eviews软件输出结果如表2所示：

表2 变截距的固定效应模型OLS估计结果

根据Eviews软件输出结果可知：在10%的显著性水平下，解释变量都显著，固定效应模型中修正的R2为0.9301，F统计量的值为90.3662。

3.1.3 利用似然比检验，对混合效应模型和固定效应模型进行取舍H0∶固定效应模型是冗余的；H1∶固定效应模型不是冗余的。软件输出结果如表3所示：

表3 软件输出的似然比检验结果

由表3中的结果可知，在5%的显著性水平下，拒绝原假设，接受备择假设，所以应选择固定效应模型。

3.1.4 对模型（4）建立随机效应模型

类似固定效应模型，随机效应模型也假定：

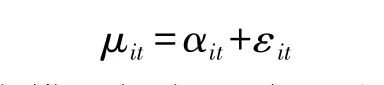
但与固定效应模型不同的是，随机效应模型假定αi与εit同为随机干扰项。

随机效应模型可以如下表示：

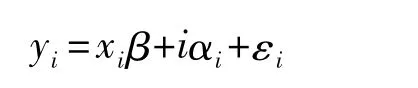
其中yi和εi均为T×1向量；xi是T×K矩阵；αi是一个随机变量，代表个体的随机效应。软件输出结果如表4所示：

表4 变截距的随机效应模型OLS估计结果

根据Eviews软件输出结果可知：随机效应模型中修正的R2为0.8976，F统计量的值为206.9527，在5%的显著性水平下，两个解释变量都显著。

3.1.5 进行Hausman检验，确定选择随机效应还是固定效应模型

H0∶选择随机效应模型；H1∶选择固定效应模型。

软件输出结果如表5所示：

表5 软件输出的Hausman检验结果

由表5所示，在5%的显著性水平下，应该接受原假设，即随机效应模型的系数与固定效应模型的系数没什么差别，故应选择随机效应模型。

3.2 结果解释

由表4的随机效应模型的OLS估计结果，我们可以得到在5%的显著性水平下，解释变量EXP、S对被解释变量的影响均是显著的。并且修正的R2比较大，数值为0.897582，模型拟合优度好。根据回归结果，可得估计的回归方程为：

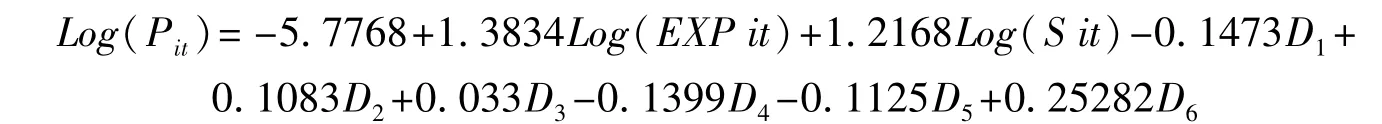
其中虚拟变量D1，D2，D3，D4，D5，D6的定义是：Di，如果属于第i个体，i＝shanxi，anhui，jiangxi，henan，henan，hubei，hunan，Di＝0，其它。

通过面板数据模型估计的常数项，还包括一个固定的部分，即估计的回归方程中的系数为-5.7768，这部分代表各个省份的共同特征，然而可以用来代表技术创新效率的可变截距项的系数的差别很明显，说明中部六省在技术创新能力方面存在巨大差距。湖南省的科研创新基础雄厚，能力较强，在中部地区六省中居第一；安徽省的科技创新能力在六省中排第二，是因为最近这几年安徽省大力引进先进技术，培养科技创新人才，引进大批科技优秀人才；江西省居第三，河南、湖北、山西的技术创新能力相对薄弱，尤其是山西实力最弱。中部六省的技术创新能力存在差异，在某种程度上正是技术水平发展不平衡的结果。中部六省的技术存在分化现象，而这种现状是由很多因素共同造成的，既有历史的原因，又有改革开放以来各省实施不同的发展战略，以及在实施中部崛起战略后，各省的发展规划不同等。

［1］中国科技发展战略研究小组.中国区域创新能力报告［M］.北京：科学出版社，2010.

［2］李子奈.高等计量经济学［M］.北京：清华大学出版社，2000.

［3］郭国峰，温军伟，孙保营.技术创新能力的影响因素分析—基于东部六省面板数据分析［J］.数量经济技术经济研究，2007（9）：134-143.

梁艳（1984-），女，安徽舒城人，安徽财贸职业学院基础部讲师，从事运筹学和应用数学研究。

207

A

2095-0063（2013）06-0112-03

2013-10-11