具有变指数反应项和正初始能量p-Laplce方程解的爆破

高文杰，刘国清

（1.吉林大学数学研究所，吉林长春130012；2.大庆师范学院数学科学学院，黑龙江大庆163712）

具有变指数反应项和正初始能量p-Laplce方程解的爆破

高文杰1，刘国清2

（1.吉林大学数学研究所，吉林长春130012；2.大庆师范学院数学科学学院，黑龙江大庆163712）

研究了具有变指数反应项p-laplace方程解的爆破。通过构造能量泛函方法发现当初始能量为正时，具有变指数源函数的p-laplace方程解在有限时刻爆破。

p-laplace方程；正初始能量；解的爆破

0 引言

本文考虑如下初边值问题

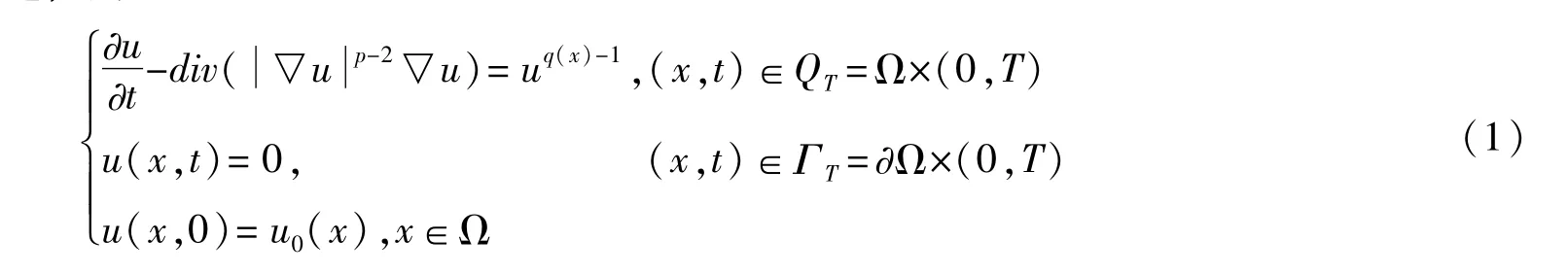
其中Ω⊂RN，（N≥1），∂Ω充分光滑。非线性科学、物理学、流体力学、生物学和医学等学科大量出现的数学模型以及来自于工业问题的数学模型通常归结为一些具退缩性或奇性的非线性抛物型或椭圆型偏微分方程以及非线性泛函偏微分方程，其解的存在性、唯一性、渐近性及解的结构与性质等方面的研究在理论及实际应用中都具有十分重要的意义，详细的内容可以参看文献［1-3］。特别地，一类源于非牛顿流体力学中的非线性发展方程（即经典p-Laplace方程从上世纪八九十年代开始便被许多学者研究.而关于此类问题解的性质例如存在性、唯一性、正则性等的研究已经比较完善，详细的内容可以参看文献［4-6］。在最近十年中，许多作者开始研究p-Laplace方程中指标p为空间变量和时间变量的函数时，其相应问题解的性质，其中指数p描述电流变液流体学中有关非均匀物质在外电场影响下的剧烈变化，即p是外电场的函数。事实上，通过物理学中的基本理论易知电场函数满足Maxwell方程，而通过求解Maxwell方程我们发现指数p是自变量的函数。因此我们所研究的问题是对实际问题的数学模型化。此外，从实际理论及纯数学方面来看，关于这类问题的研究都有意义的，具体数学推导及各项所代表的物理意义可以参看文献［7，8］。关于反应项中指数依赖自变量时，解的爆破问题，文献［4］的作者利用特征函数方法对Laplace方程具有Dirichlet边值问题进行了研究。对于涉及p-Laplace算子和变指数源函数的非线性发展方程解的爆破性质，目前还没有文献参考。由于反应项中q（x）的引入，使得方程缺乏正齐次性，从而使得文献［1］所使用的方法不能应用于讨论问题（1）解的爆破性质。为了克服这个困难，本文通过构造新的过渡函数和合适的嵌入定理以及精确的计算克服了这个困难，进而获得了所研究问题的解在初始能量为正时在有限时刻爆破。

为了讨论问题的方便，本文引进如下符合

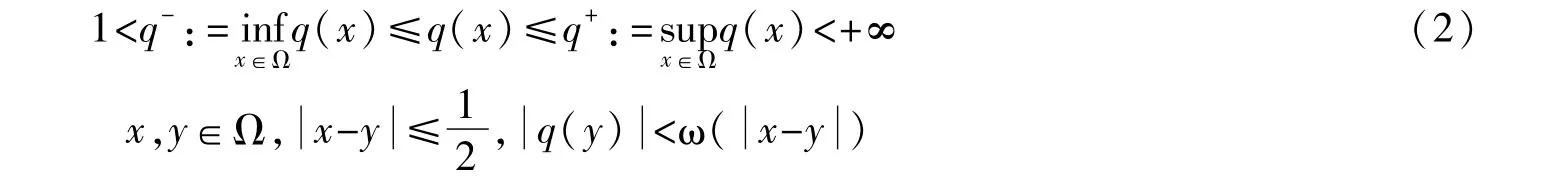
这里

Lq（.）（Ω）表示如下可测函数空间：

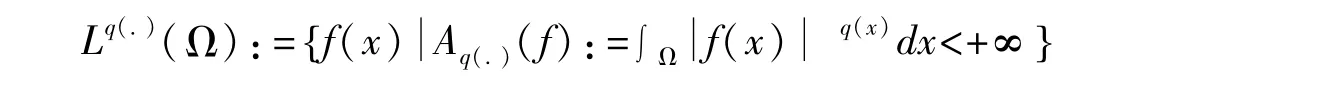
其范数为

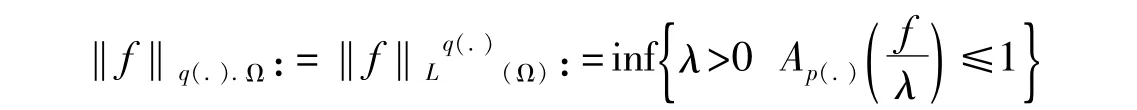
容易验证Lq（.）（Ω）是Banach空间，见文献［5］。从范数定义有

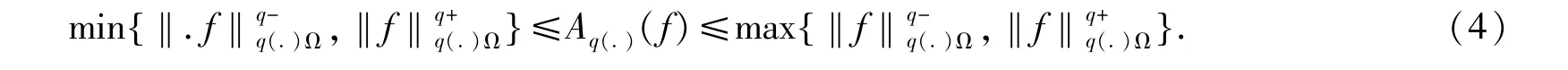
设B是嵌入不等式中的嵌入常数，则由文献［9，10］可知

即等价于

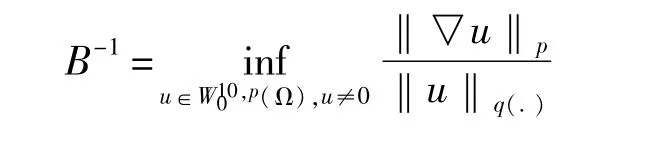
令

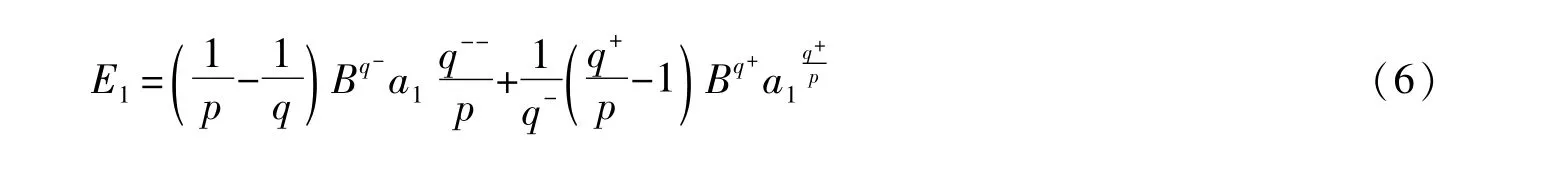
其中a1满足

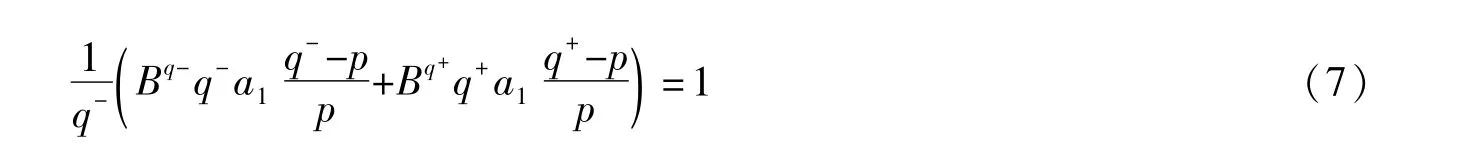
此外，设

1 主要引理

引理1：函数E（t）关于时间变量t是非增的。

证明：由问题（1.1）及（1.10），对函数E（t）求导得

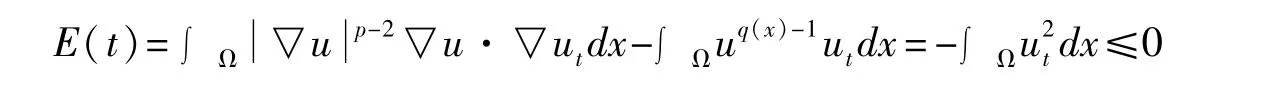
故引理1得证。

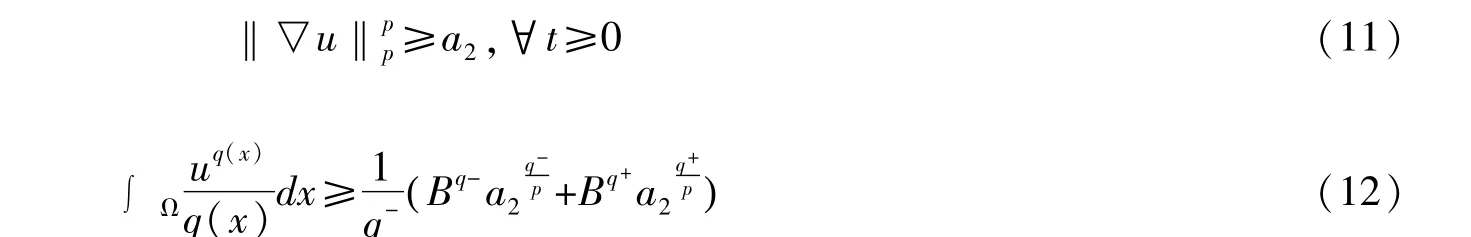
证明：从（5）和（10）我们有

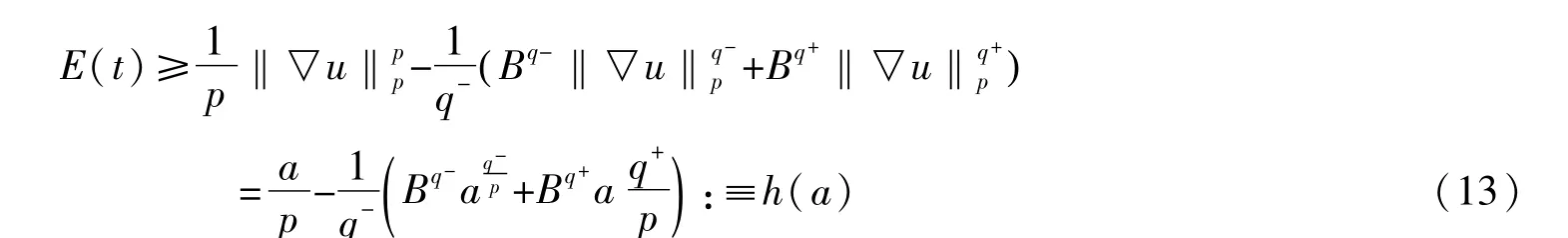
其中a＝‖▽u‖pp。容易验证h（a）在区间（0，a1）上单调递增，在区间（a1，+∞）上单调递减且h（a）→-∞，当a→+∞时，且e（a1）＝E1，其中E1，a1的定义见式（6）和（7），由于E，则存在使得h（a2）＝E（0）。令a0＝‖▽u0‖pp，从（2.3）我们有h（a0）≤E（0）＝h（a2），进一步我们还可以证明a0≥a2。

假设式（11）不成立，即存在t0＞0使得‖▽u（·，t0）‖pp＞a2，由于‖▽u（·，t）‖pp连续性，我们有E（0）＝h（a2）＜h（‖▽u（·，t0）‖）≤E（t0），这与引理1矛盾，故式（11）成立。

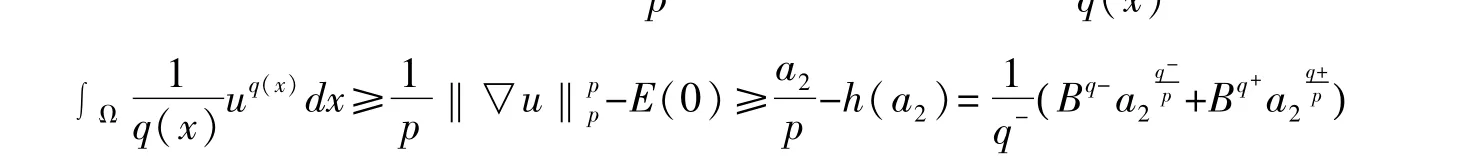
故式（12）成立。

引理3：对所有t＞0，均有

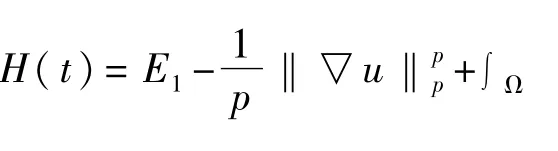
2 主要结论

定理1：假定q（x）满足式（12）和（13），且下面条件成立：

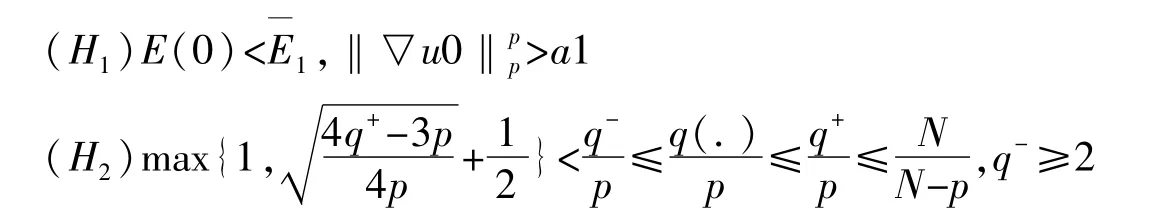
则问题（1）的解在有限时刻爆破。

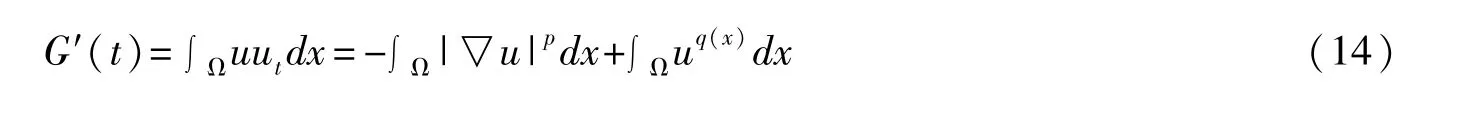
从式（10）和（13），我们有

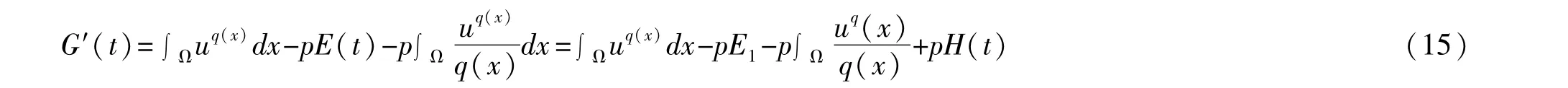
其中

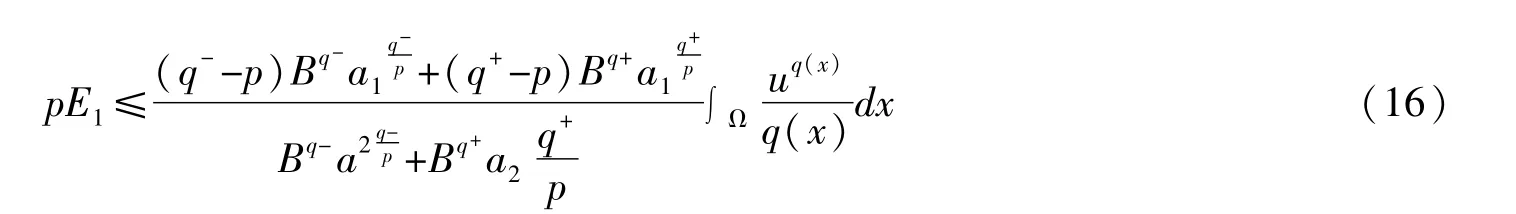
结合式（15）和（16）有

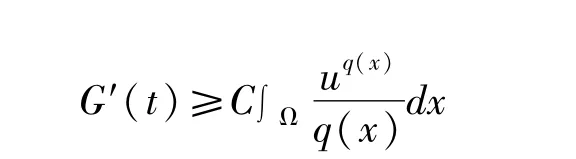
3 结语

本文研究了一类源于非牛顿流体力学中非线性发展方程解的爆破性质。我们发现由于变指数q（x）的引入，研究常指数q时所使用的方法不能应用于此问题的研究，故我们不得不寻找新的研究方法。在本文中作者通过构造新的过渡函数，获得了非线性项∫Ωuq（x）+1dx和初始能量的一个比较关系，从而证明了该问题的解在有限时刻爆破。不足的是不能证明E—1是最优的，即当初始能量大于E—1时，该问题的解在有限时刻不爆破。这将是我们今后继续研究的一个课题。

［1］Samarskii A.A.，Kurdyumov S.P..Blow-Up in Problems for Quasilinear Parabolic Equations，Nauka，Moscow［M］.Berlin：Walter de Gruyter，1995.

［2］Levine H.A..Some nonexistence and instability theorems for solutions of formally parabolic equations of the forP＝-Au+F（u）［J］.Arch.Ratioal Mech.Anal.，1973，51：371-386.

［3］Zhao J.N..On the Cauchy problem and initial traces for the evolution p-laplacion equationswith strongly nonlinear sources［J］.J.Diff.Eqs.，1995，121：329-383.

［4］Liu W.J.，Wang M.X..Blow-up of the solution for a p-Laplaican Equation with positive initial energy［J］.Acta.Appl.Math.，2008，103：141-146.

［5］Dibenedetto E..Degenerate parabolic equations［M］.New York：SpringerVerlag，1993.

［6］Zhao J.N..Existence and nonexistence of solutions for u.J.Math.Anal.Appl.，1993，172：130-146.

［7］Ruzicka M..Electrorheological fluids：Modelling and Mathematical theory，Lecture Notes in Math［M］.Berlin：Springer，2000.

［8］Acerbi E.，Mingione G.，Seregin G.A..Regularity results for parabolic systems related to a class of Non Newtonian fluids［J］.Annal de lInstitut Henri Poincare-Analyse Non Lineaire，2004，21：25-60.

［9］Diening L.，Harjulehto P.，Hasto P.，et al.Lebesgue and Sobolev spaces with variable exponents，Lecture Notes in Mathematics［M］.Heidelberg：Springer-Verlag，2011.

［10］Ferreira R.，de Pablo A.，Prez-Llanos M.，et al.Critical exponents for a semilinear parabolic equation with variable reaction［J］.Proc.Roy.Soc.Edinburgh Sect.A，2012 142（5）：1027-1042.

高文杰（1956-），男，吉林长春人，吉林大学数学研究所教授，博士生导师，从事应用数学研究。

国家自然科学基金（11271154）；黑龙江省自然科学基金（A200813）。

O175.8

A

2095-0063（2013）06-0068-04

2013-06-25