论检验数在求解对偶问题中的作用

展丙军，卢树强

（大庆师范学院数学科学学院，黑龙江大庆163712）

论检验数在求解对偶问题中的作用

展丙军，卢树强

（大庆师范学院数学科学学院，黑龙江大庆163712）

在求解线性规划中，检验数起到判定是否最优解的作用。实际上，在求解对偶问题中，检验数也起到很重要的作用，它和对偶问题的解存在着密切的关系，甚至直接就是对偶问题的解；利用检验数往往可以直接或间接地写出对偶问题的解，它是原问题和对偶问题有关解方面的桥梁，在求解对偶问题时，起到了重要的作用。

线性规划；对偶问题；检验数；单纯形乘子

1 相关定理

引理1［1］：线性规划

引理2［1］：LP问题的检验数向量为：λ＝CTBB-1A-CT，其中各个分量为检验数。求最小值问题时，λ＝CTBB-1A-CT≤0，求最大值问题时，λ＝CTBB-1A-CT≥0。（注：因为原问题的最优解，一定是人工变量为0的最优解，所以人工变量对应的检验数不必考虑正负）。

引理3［2］：如果一个LP问题有最优解，则它的对偶问题也有最优解，且它们的最优值相等。设原始问题的最优解x0所对应的基为B，则对应的单纯形乘子CBB-1就是对偶问题的最优解。

注：本文所有矩阵A都是m×n的，且秩为m。

2 检验数在求解对偶问题中的作用

（1）若A＝（N0，Im，Im）时，Im为m阶单位矩阵，可作为初始基，将-Im称为初始负基。则

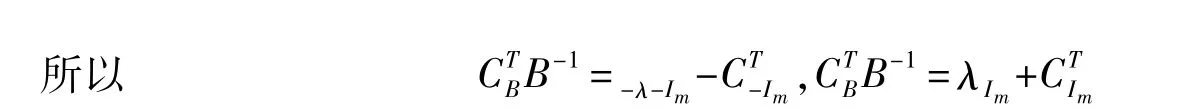
由引理3知，上式就是对偶问题的解。另外，从上面的推导可知，该结论与求最大值问题，还是求最小值问题无关，Im的出现多伴随求最大值问题，而-Im的出现多伴随求最小值问题。

所以，可以得到下面的重要结论：

定理1：若A＝（N0，-Im，Im），则互为对偶问题中任何一个的最优单纯形表格（或矩阵）中，初始基变量（与Im对应的）对应的检验数与这些变量在原始目标函数中的系数之和（即λIm+CTIm），就是对偶问题的解。初始负基变量（与-Im对应的）对应的检验数与这些变量在原始目标函数中的系数之和的相反数（即-λ-Im-CT

-Im），也是对偶问题的解。

推论：若松弛变量个数为m，或者人工变量个数为m（即CTIm＝0），则它们对应的检验数就是对偶问题解。若剩余变量个数为m时（即CT-Im＝0），则剩余变量对应的检验数的相反数就是对偶问题的最优解。

由此定理，容易得到当A＝（N0，-Im）或A＝（N0，Im）时相应的推论，这里略。

也可以换一种方式解释上面的结果，比较A＝（N0，Jm）和A＝（N0，-Im，Im）的差异，显然取-Im所对应的解的前k个，取Im所对应的解的后m-k个就得到A＝（N0，Jm）下所对应对偶问题的解了。于是，有下面的结论：

特别地，若k＝0时，则A化为A＝（N0，Im），若k＝m时，则A化为A＝（N0，-Im），那么对偶问题相应的解与定理1中的结论是一致的。

推论：若松弛变量个数（或者人工变量个数）与剩余变量个数之和为m时，这时对应的原目标函数的系数ci＝0（i＝n-m+1，n-m+2，…，n），则对偶问题的解可用下面的公式来表示

下面利用前面的理论解决一个具体问题。

例［1］：求解下面的线性规划问题及其所对应的对偶问题

解：为了较好地说明本文的结论，再引两个人工变量（非负）x4，x5，则化为

（a）利用引理1，写出对应矩阵并对其进行初等变换

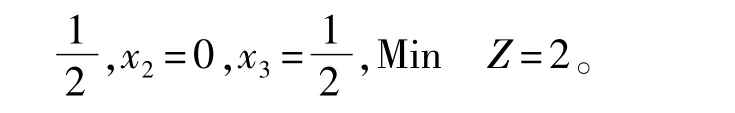
（c）由已知及（a）有C＝（1，2，3，0，0）T，λ＝（0，-1，0，-1，3）T。

由定理1的推论，对偶问题的解为（ω1，ω2）＝（λ4，λ5）＝（-1，3）

再由定理2也可以得到对偶问题的解为：（ω1，ω2）＝（-λ2-c2，λ3+c3）＝（-（-1）-2，0+3）＝（-1，3）

3 结语

本文给出了线性规划问题的系数矩阵在A＝（N0，-Im，Im）、A＝（N0，Jm）等特殊情况下，对偶问题的解与原问题最优解所对应的检验数之间的联系，通过这种联系，往往很容易从原问题的最优单纯表（或矩阵）中直接得到对偶问题的解。其实，本文中系数矩阵出现的各种形式是经常出现的，特别在化标准形时常常引入松弛变量、人工变量、剩余变量，这样经常出现单位阵或半单位阵或负单位阵，利用本文所给出的结论，很轻松地得到对偶问题的最优解。将此成果应用于求解相关问题，带来很大方便，可大大减少计算量，效果是显而易见的。

［1］展丙军.单纯形法的改进及其应用［J］.大庆师范学院学报，2007（2）：5-8.

［2］刁在筠，刘桂真，宿洁，等.运筹学［M］.北京：高等教育出版社，2007：23-24，47-48.

［3］吴祈宗.运筹学［M］.北京：机械工业出版社，2002.

［4］宁宣熙.运筹学实用教程［M］.北京：科学出版社，2002.

展丙军（1963-），男，河南长垣人，大庆师范学院数学科学学院教授，从事运筹学研究。

O221.1

A

2095-0063（2013）06-0052-03

2013-07-08