主动移频式孤岛检测法产生稀释效应机理的分析

谢 东，张 兴

(合肥工业大学电气与自动化工程学院，安徽 合肥 230009)

0 引言

由于孤岛效应会对分布式发电系统[1]造成多种有害影响，所以孤岛检测是并网逆变器必须具备的功能。分布式发电系统孤岛检测方法主要分为被动式与主动式两类[2]。被动法阈值难确定，且有较大检测盲区（Non-Detection Zone，NDZ）。主动法弥补了被动法的缺点，尤其是基于频率或相位扰动的主动移频式孤岛检测法因操作简单、检测盲区小而得到广泛应用。在单逆变器组成的分布式发电系统中，该法能可靠检测出孤岛，但在多逆变器并联分布式系统中，各逆变器产生的扰动相互抵消，即所谓的稀释效应，使孤岛检测失败。关于主动移频式孤岛检测法在多逆变器并联系统中的检测效果，已有相关文献进行了研究。文献[3]分析了多逆变器并联系统中主动移频式孤岛检测法的性能，但并没有涉及稀释效应的问题。文献[4-5]虽然指出系统中各逆变器产生的扰动相互抵消，有可能使孤岛检测失效，但并未就稀释效应问题展开研究。为此，笔者研究分析了主动移频式孤岛检测法稀释效应产生机理，以期为更好地使用该检测法提供有益的参考。

1 主动移频式孤岛检测法概述

主动移频式孤岛检测法主要包括主动频率偏移法（Active Frequency Drift，AFD）、Sandia频率偏移法（Sandia Frequency Shift，SFS）和滑模频率偏移法（Slip-mode Frequency Shift，SMS）等。

1.1 主动频率偏移法（AFD法）

AFD法的原理[6]是通过并网逆变器向电网注入略微变形的正弦电流，使电网断开后，公共耦合点（PCC）电压的频率被强迫向上或向下偏移直至超过设定阈值而检测出孤岛。以向上频移为例，控制逆变器输出电流为畸变的斩波波形，如图1所示。

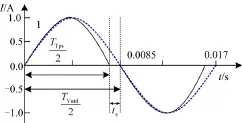
图1 AFD孤岛检测法的电流波形Fig. 1 Current waveform of AFD islanding detection

图1 中，TTPV是光伏逆变器输出电流的周期，TVutil是PCC点电压的周期。由图可知，前半个周期，光伏逆变器输出电流的频率略微高于 PCC点电压的频率。电流为零后，在Zt时段保持零值直到后半周期的起始点；后半周期情况类似，当输出电流再次达到过零点，同样将零值保持一段时间。图1所示电流波形，其斩波系数可定义为

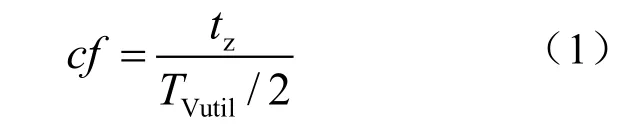
孤岛发生后，光伏逆变器输出电流可以看作源电流，PCC点的电压响应将跟随失真的电流波形，以比纯正弦激励的响应更短的时间到达上升过零点，这也就意味着后一个周期电压响应的频率总是比前一个周期电压响应的频率有所提高。这种过程一直持续到频率偏移足够大从而触发过频保护，实现了孤岛检测功能。

与被动式反孤岛策略相比，AFD法具有更小的NDZ，但畸变的电流降低了并网逆变器输出电能的质量，并且不连续的电流波形还可能导致射频干扰。在多逆变器并联的光伏系统中，若采用 AFD法进行孤岛检测，必须统一不同并网逆变器的频率偏移方向，否则会因稀释效应导致孤岛检测失效。另外，光伏系统所接本地负载是阻性或感性负载时，检测盲区较小；当本地负载呈容性时，因负载电压滞后于负载电流，对PCC点电压的频率具有向下偏移的作用，与 AFD法向上偏移电压频率的作用相互抵消，有可能因此检测不出孤岛，所以检测盲区较大。

1.2 Sandia频率偏移法（SFS法）

针对AFD法NDZ仍较大的缺点，美国Sandia实验室首先提出带正反馈AFD法，即Sandia频率偏移法[7]。其斩波系数定义为

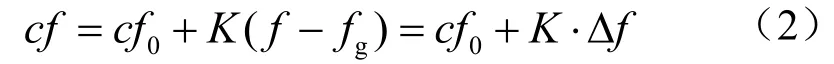
式中：0cf为无频率误差时的初始斩波系数；K为正反馈增益；f与gf分别为PCC点电压频率与电网电压额定频率。上式中，第二项即为促使频率偏移的正反馈项，频率偏差越大，正反馈越强。在并网运行的情况下，电网的稳定性能够阻止频率的变化；当孤岛发生时，由于引入正反馈机制，加速了频率偏移，从而提高了孤岛检测速度，减小了检测盲区。SFS法的关键是选择合适的正反馈增益K，使在维持系统稳定的前提下，频率偏移的速度加快。

SFS法优点是比 AFD法的孤岛检测性能高很多，不仅频率的偏移的速度加快，而且在频率变化为负值时可使频率偏移减小，所以在相同频率偏移下，NDZ更小。另外，在多逆变器并联运行条件下，各逆变器间的影响比AFD法小。

SFS法缺点与AFD法一样，负载的性质对频率的偏移有影响，可能会减缓甚至抵消频率的变化，从而降低了SFS法孤岛检测的性能。

1.3 滑模频率偏移法（SMS法）

SMS法[8]与SFS法都通过引入正反馈来提高孤岛检测效率并减小检测盲区，SMS法与SFS法的区别是对逆变器输出电流的相位而不是频率进行扰动，控制逆变器的输出电流相位为频率偏差函数

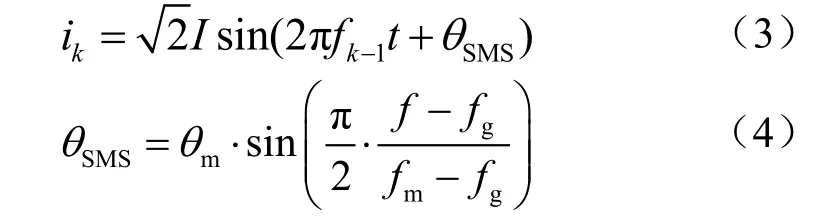
式中： fm是对应于最大相移角mθ的工作频率；f与fg分别为PCC点电压频率与电网电压额定频率。

并网运行时，系统的频率被锁定为电网电压频率 fg；当断网时，如果负载相位的变化小于逆变器输出电流相位的变化[3]，即

则图2中负载相位曲线的斜率小于逆变器输出电流相位角SMSθ曲线的斜率，这将使PCC点电压的频率从fg处发生偏移（上移还是下移取决于本地负载的性质）。频率偏差越大，SMSθ就越大，这种正反馈机制会使相位进一步发生变化，使电压频率到达新的稳定工作点。只要新的稳定工作点频率超出OFR/UFR保护的阈值范围，就可检测出孤岛。

图2 SMS法电流相位曲线与负载相位曲线Fig. 2 SMS phase curve and load phase curve

SMS法优点是检测效率很高，NDZ很小；检测效率不受多逆变器并联的影响。SMS法缺点是由于需要修正逆变器输出电流的相位，会影响输出电能质量；当负荷曲线的倾斜幅度大于 SMS曲线，则可能在过/欠频的动作区内有稳定运行点，导致孤岛检测失败。

2 主动移频式孤岛检测在多逆变器并联运行条件下稀释效应的产生

随着可再生能源利用率不断增长，越来越多的分布式系统采用多逆变器并联结构，多机并联运行时孤岛检测性能，成为一个关注热点，而多机并联时孤岛检测的稀释效应，是值得研究的问题。以图3所示的多机并联系统为例，分析主动移频式孤岛检测产生稀释效应的情况。图中L1为本地RLC并联负载。

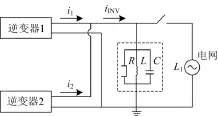
图3 2台并网逆变器组成的多机系统Fig. 3 System with two grid-connected converters

2.1 采用向上移频AFD法与SMS法逆变器各一台

设使用AFD法的逆变器为本地负载提供了比例为KAFD的有功功率,则两逆变器输出电流可定义为

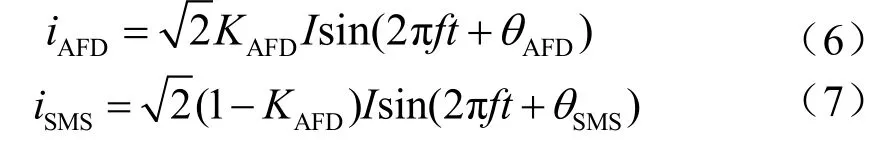
其中，采用 AFD法的并网逆变器输出电流的初相位SMSθ可由图1得出，为

由上述表达式，若两台并联逆变器等效为一台逆变器，则等效的并网逆变器输出电流的初相角为

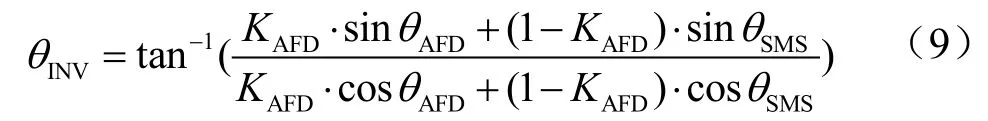
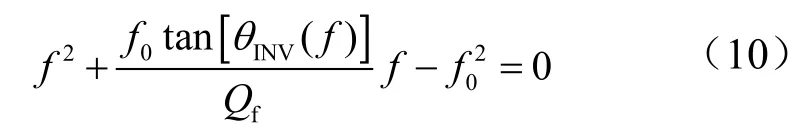
由式（10），采用AFD法的并网逆变器有功出力的比例KAFD分别为0.2、0.5、0.8时，等效并网逆变器检测盲区如图4所示。图中有关参数设置如下：θAFD=3o，θm=10o，fm－fg=3 Hz， fg=50 Hz。图 4 表明, 检测盲区的上边界在三种情况下是不变的,但下边界则随着采用 AFD法逆变器有功出力比例的增加而下移,检测盲区也因此增大。这是因为当f - fg＞0时，AFD法与SMS法均有向上移频作用；当f-fg＜0时，AFD法试图使频率上移，而SMS法则产生了频率下移的作用，两者互相抵消，使检测盲区增大。

若将SMS法改用SFS法，即向上移频AFD法与SFS法逆变器各一台，同样会出现稀释效应。因为SMS法与SFS法的相角都是频率偏差的函数，两者使频率随负载特性向上或下移动，当f - fg＜0时，AFD法与SFS法移频作用相抵消而增大检测盲区。

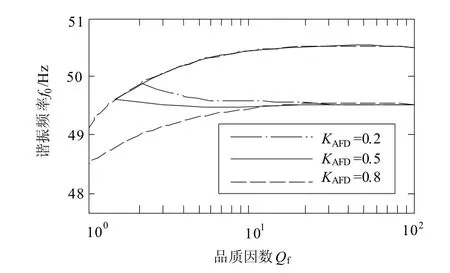
图4 同时采用AFD法与SMS法的检测盲区Fig. 4 NDZ with both AFD and SMS methods

2.2 采用SFS法与SMS法逆变器各一台

若使用SFS法的逆变器为本地负载提供了比例为KSFS的有功功率,则两台逆变器输出电流分别为

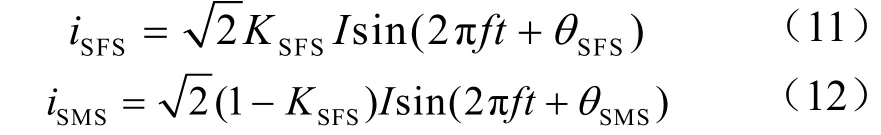
式(11)中并网逆变器输出电流的初相位SMSθ为

由式（11）~式（13），两台并联逆变器等效为一台逆变器后，等效逆变器输出电流的初相角为

如果两台逆变器均使用 SFS法或均使用 SMS法，则情况类似，两台逆变器因扰动方向一致而维持正反馈移频作用，从而能够检测出孤岛[4-5,9]。

3 主动移频式孤岛检测法稀释效应机理分析

上一节分析表明，采用带正反馈的主动移频式孤岛检测在多逆变器并联运行情况下受稀释效应影响很小，依然可以保持良好的检测性能。但在分布式发电现场，有时也会出现因稀释效应造成孤岛检测失败的事例。如美国曾经发生过主网断开后分布式系统继续向本地负载供电，1 min后才跳闸保护的事故。其原因就是分布式系统孤岛检测产生了稀释效应。实际应用中之所以会出现稀释效应，与上述结论不符，是因为上节的结论是在理想条件下得出的，没有考虑各逆变器检测同一电网频率时可能存在一定的传感器检测误差。还是以两台逆变器并联运行为例，考虑最恶劣的情况，即两台逆变器的传感器存在幅值相等、符号相反的检测误差时，产生稀释效应的情况。

3.1 两台逆变器均使用SFS法稀释效应分析

设两逆变器均用SFS孤岛检测法，为分析简化，两台逆变器各分担一半的负载有功功率，且斩波系数表达式 cf= cf0+K(f－fg)中采用相同的 cf0和增益K。若 PCC点电压的实际频率为 f，两台逆变器检测出的频率分别为f1和f2，两台逆变器输出电流分别为

则等效逆变器的电流为

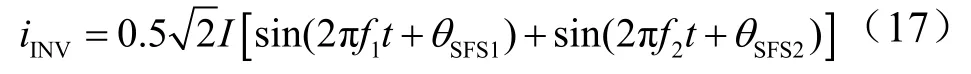
若传感器检测误差较小，即 f1≈f2≈f ，则式（17）近似写为

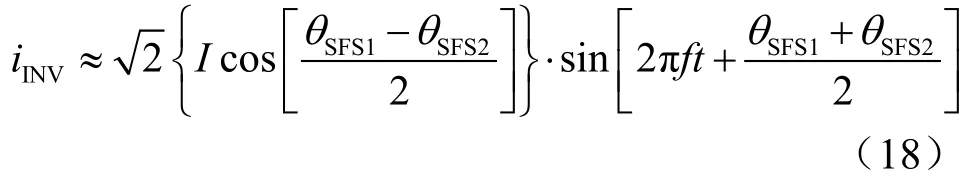
则等效逆变器的移频相角为

若传感器检测误差造成Δf1=－Δf2，则

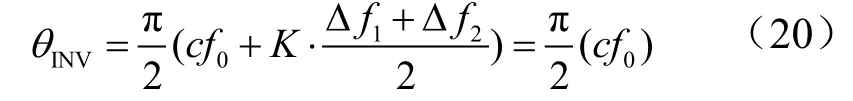
可见等效逆变器移频相角中正反馈分量下降为0，稀释效应较严重，有孤岛检测失败的可能。另外，式（20）表明，等效逆变器此时可以看成采用AFD法的逆变器，若系统中还并联了其他逆变器，而这些逆变器有功出力明显小于等效逆变器有功出力，根据图4，此时NDZ较大，孤岛检测可能失败。

3.2 两台逆变器均使用SMS法稀释效应分析

设两台采用SMS法的逆变器检测出的PCC点电压的频率分别为f1=f＋Δfe、f2=f－Δfe，即传感器存在等值异号的检测误差，两台逆变器各分担一半的负载功率且θSMS表达式中采用相同的θm和fm值，两台逆变器输出电流分别为

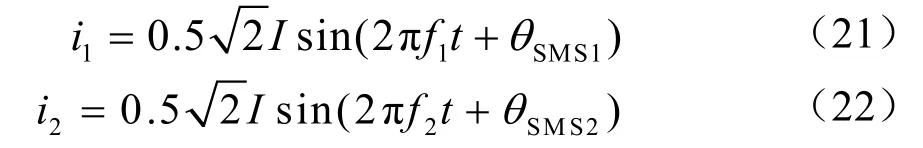
当传感器检测误差较小时， f1≈f2≈f，则等效逆变器的电流为

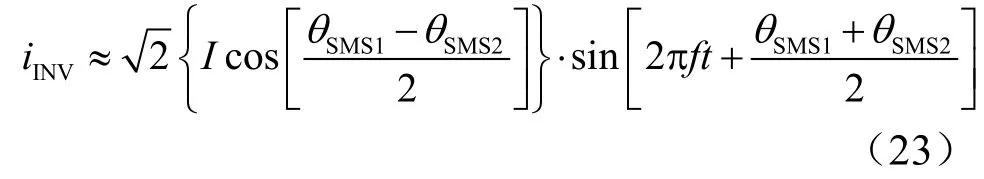
所以，等效逆变器的移频相角为

由上式，等效逆变器的最大相移角为

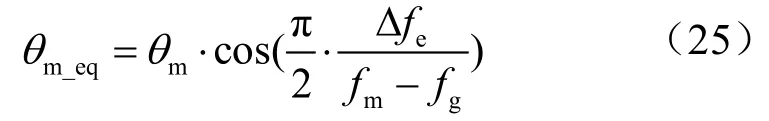
将式（25）的θm_eq和式（4）的θm比较可看出，传感器检测误差会减少最大相移角θm的幅值 ，也就是减小了频率偏移的正反馈强度，说明两逆变器并联运行存在稀释效应。然而，即使测量误差 Δfe取相对较大的值(0.5 Hz), 使用SMS法作为孤岛检测方案时，最大相移角(θm_eq)仅比θm下降了3.4 % ，检测盲区没有明显的变化。图5为频率测量误差取不同值时检测盲区示意图(θm= 10°、 fm– fg=3 Hz)。由图可知，虽然频率检测误差使两并网逆变器产生的扰动可能相互抵消，但对孤岛检测性能影响很小。

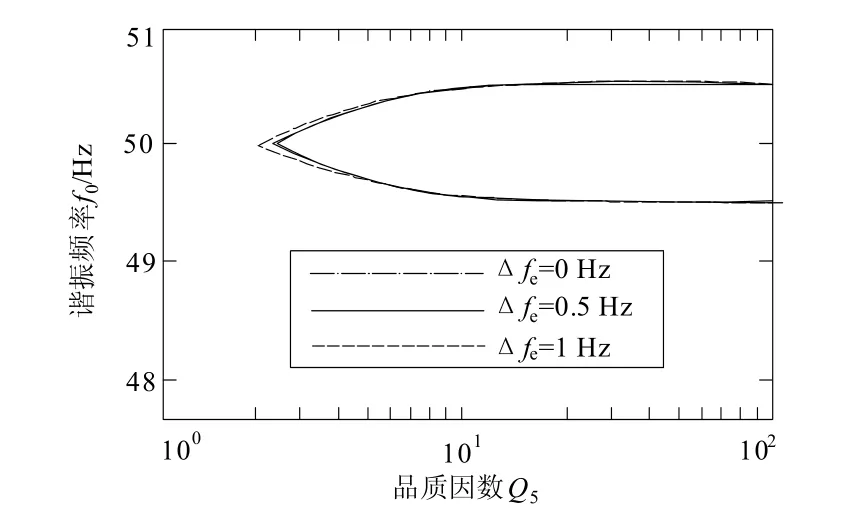
图5 不同频率检测误差时SMS法的检测盲区Fig. 5 NDZ of SMS method with different detective error

3.3 稀释效应产生机理与仿真验证

前面的分析表明，采用SFS孤岛检测法的多逆变器并联比采用SMS法时稀释效应严重，孤岛检测失败的可能性增大，这与两者频率扰动的机理不同有关。频率扰动是一种不稳定因素，在孤岛形成后，它是使频率产生偏移的一个主要原因，而频率扰动越强，则频率偏移速度越快。频率扰动的强度，与频率偏移角的大小有关。考虑电流总谐波畸变率不大于5%，SFS法中cf0取值不超过5%[10]，由式（20），在传感器检测误差影响下，采用SFS法时等效逆变器最大频率偏移角为（π/2）×0.05≈0.0785 rad；由式（25），若θm=10o，则采用SMS法时等效逆变器最大频率偏移角为 10×(1－0.034)×(2π/360)≈0.17 rad，明显大于采用SFS法时的最大频率偏移角。

另外，SFS法与SMS法都是通过引入频率扰动的正反馈来加快频率偏移。式（13）表明，由于SFS法相位扰动角θSFS与频率偏差△f是线性关系，在传感器检测误差等值异号时，会使两逆变器的频率扰动信号互相抵消而失去正反馈扰动特性；式（4）表明SMS法相位扰动角θSMS与频率偏差Δf是非线性关系，出现等值异号的频率检测误差时，两逆变器的频率扰动信号一般不会互相抵消，即频率扰动的正反馈依然存在，从而采用SMS法的多逆变器并联运行时受稀释效应影响相对较小。

为验证上述分析结果，采用Matlab/Simulink对两台逆变器并网运行系统孤岛检测性能进行仿真。采用参数如下：电网电压有效值220 V、额定频率fg= 50 Hz，SFS法中cf0= 0.05、K = 0.07，SMS法中 θm= 10o、fm– fg= 3 Hz，频率保护动作阈值为（50±0.5）Hz。另外，两台逆变器各输出功率500 W，与本地RLC并联负载功率匹配，负载品质因数Qf=2.5。

图6是两台逆变器采用SFS法没有传感器检测误差时的孤岛检测情况。该图横轴表示时间，单位为 s；纵轴电流单位为 A、电压单位为 V、频率单位为Hz。由图6可知，由于逆变器输出功率与本地负载功率匹配，断网前电网电流只有很小的一点谐波电流。0.1 s时产生孤岛，电网电流完全为0，0.24 s时检测出孤岛，两台逆变器电流及PCC点电压降为0。

图7是两台逆变器采用SFS法传感器检测误差为±0.6 Hz时的孤岛检测情况。由图可知，由于传感器检测误差造成了严重稀释效应，频率偏移缓慢，2 s时尚未达到阈值，根据国标GB/T 19939—2005光伏系统要在2 s内检测出孤岛的技术要求[11]，检测失败。

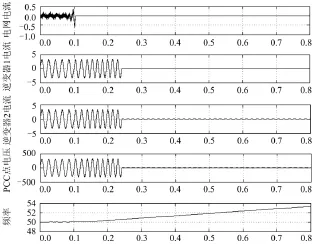
图6 两台逆变器均用SFS法没有频率检测误差Fig. 6 Two SFS method inverters without detective error

图7 两台逆变器均用SFS法频率检测误差为±0.6 HzFig. 7 Two SFS method inverters with detective error ±0.6Hz

图8 是两台逆变器采用SMS法没有传感器检测误差时的孤岛检测情况。图8表明，在0.1 s断网后，0.32 s时两台逆变器电流及PCC点电压降为0，孤岛检测成功。

图9是两台逆变器采用SMS法传感器检测误差为±0.6 Hz时的孤岛检测情况。由图可知，在0.1 s断网后，0.58 s时成功检测出孤岛。说明采用SMS法时，受稀释效应的影响较小。

图10是两台逆变器采用SMS法传感器检测误差为±3 Hz时的孤岛检测情况。同图7一样，由于稀释效应，2 s时尚未检测出孤岛。该图说明，当传感器检测误差非常大时，采用SMS法的两台逆变器同样会产生稀释效应使扰动互相抵消，导致孤岛检测失败。但是，传感器一般不会产生这么大的检测误差。

图8 两台逆变器均用SMS法没有频率检测误差Fig. 8 Two SMS method inverters without detective error

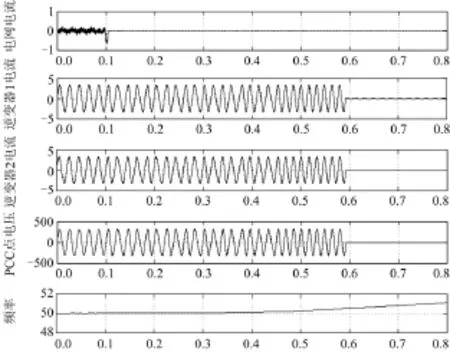
图9 两台逆变器均用SMS法频率检测误差为±0.6 HzFig. 9 Two SMS method inverters with detective error ±0.6Hz

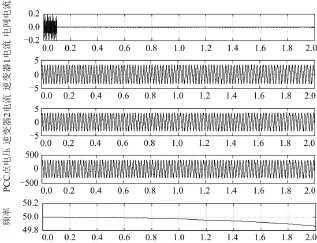
图10 两台逆变器均用SMS法频率检测误差为±3 HzFig. 10 Two SMS method inverters with detective error ±3Hz

4 结论

本文分析了多逆变器并联运行时主动移频式孤岛检测法产生稀释效应的机理，得出结论如下：

1）AFD法施加的是单方向的扰动，而SMS法与SFS法的都使频率随负载特性向上或向下移动。因此，多逆变器并联系统中同时存在AFD法与带正反馈的SMS（或SFS法）时，逆变器的频率扰动相互影响产生稀释效应，从而降低孤岛检测能力。采用AFD法的逆变器有功出力越多，孤岛检测盲区越大。因此，多逆变器并联系统孤岛检测应多采用带正反馈的主动移频法。

2）扰动方向一致且没有频率检测误差时，SFS法和 SMS法在多逆变器并联运行条件下可以保持良好的孤岛检测性能。

3）扰动方向一致但存在频率检测误差时，SFS法在多逆变器并联运行时，会因为稀释效应导致孤岛检测失败，而SMS法受稀释效应影响较小，检测性能没有产生明显下降。

[1] 贺眉眉, 李华强, 甘立勇, 等. RLC负荷模型分布式发电孤岛检测方法研究[J]. 电力系统保护与控制, 2011,39(6): 7-11.HE Mei-mei, LI hua-qiang, GAN Li-yong, et al.Islanding detection scheme evaluation for RLC load distributed generation[J]. Power System Protection and Control, 2011, 39(6): 7-11.

[2] 程启明, 王映斐, 程尹曼, 等. 分布式发电并网系统中孤岛检测方法的综述研究[J]. 电力系统保护与控制,2011, 39(6): 147-154.CHENG Qi-ming, WANG Ying-fei, CHENG Yin-man，et al. Overview study on islanding detecting methods for distributed generation grid-connected system[J]. Power System Protection and Control, 2011, 39(6): 147-154.

[3] 张有兵, 穆淼婕, 翁国庆. 分布式发电系统的孤岛检方法研究[J]. 电力系统保护与控制, 2011, 39(1):139-146.ZHANG You-bing, MU Miao-jie, WENG Guo-qing.Research on islanding detection of distributed power generation systems[J]. Power System Protection and Control, 2011, 39(1): 139-146.

[4] 刘方锐, 余蜜, 张宇, 等. 主动移频法在光伏并网逆变器并联运行下的孤岛检测机理研究[J]. 中国电机工程学报, 2009, 29(12): 47-51．LIU Fang-rui, YU Mi, ZHANG Yu, et al. Islanding detection evaluation for active frequency drifting methods in multiple photovoltaic grid-connected converters[J]. Proceedings of the CSEE, 2009, 29(12):47-51．

[5] 刘方锐, 段善旭, 康勇, 等. 多机光伏并网逆变器的孤岛检测技术[J]. 电工技术学报, 2010, 25(1): 167-171.LIU Fang-rui, DUAN Shan-xu, KANG Yong, et al.Islanding detection methods for multiple PV converters system[J]. Transactions of China Electrotechnical Society,2010, 25(1): 167-171.

[6] Ropp M E, Begovic M, Rohatgi A. Analysis and performance assessment of the active frequency drift method of islanding prevention[J]. IEEE Trans on Energy Conversion, 1999, 14(3): 810-816.

[7] Ropp M E, Begovic M, Rohatgi A, et al. Determining the relative effectiveness of islanding detection methods using phase criteria and nondetection zones[J]. IEEE Trans on Energy Conversion, 2000, 15(3): 290-296.

[8] Lopes L A C, Sun H. Performance assessment of active frequency drifting islanding detection methods[J]. IEEE Transactions on Energy Conversion, 2006, 21(1): 171-180.

[9] Est´ebanez E J, Moreno V M, Pigazo A, et al.Performance evaluation of active islanding detection algorithms in distributed generation photovoltaic systems:two inverters case[J]. IEEE Trans on Industrial Electronics, 2011, 58 (4): 1185-1193.

[10] 袁玲, 郑建勇, 张先飞. 光伏发电并网系统孤岛检测方法的分析与改进[J]. 电力系统自动化, 2007, 31(21):72-75.YUAN Ling, ZHENG Jian-yong, ZHANG Xian-fei.Analysis and improvement of islanding detection method for grid-connected photovoltaic inverters[J]. Automation of Electric Power Systems, 2007, 31(21): 72-75.

[11] 王斯成, 杨鸿雁, 王连贵, 等. GB/T 19939—2005光伏系统并网技术要求[S]. 中华人民共和国国家标准,2005.