快换式公交充电站短期负荷预测方法的研究

张维戈，颉飞翔，黄 梅，李 娟，李亚芬

(北京交通大学电气工程学院，北京 100044)

0 引言

近年来，能源危机与环境问题日益加剧，动力电池与车辆技术不断完善，电动汽车的规模化应用指日可待，届时电动汽车庞大的充电负荷将对城市电力调度及基础设施建设规划产生重要影响[1-3]。以当前北京奥运快换式公交充电站为参考，目前北京市公交车保有量约为2万辆有余，如果将其全部置换为电动客车，将需要近200座充电站才能满足全部车辆的充电需求。如果按车辆单位能耗及日常运营里程计算，其每日功率需求将大约达到40万kW。若考虑其他如环卫、物流、邮政等商用车，预计快换式社会公共服务车辆充电站负荷将达到北京市总负荷的3%，已经超出了北京电网总负荷2%的热备用电源。虽然当前大多数充电站只是处于小规模示范性运营阶段，但是在电动汽车良好的发展前景下，如何定量地评估电动汽车充电站负荷对电网带来的影响已经成为国内外学者共同关注的焦点。

充电站负荷作为电力负荷的一部分，对其进行负荷特征分析与短期负荷预测方法的研究，一方面，对于电力系统发电机组最优组合、经济调度、最优潮流及电力市场交易等有着重要的意义[4-6]；另一方面，给充电站自身的建设规划、能量管理、有序充电及经济性运行等提供了决策依据。因此，有必要以当前实际商业化运营中的快换式公交充电站为契机，研究快换站短期负荷预测方法，旨在为将来大规模建站时提供数据支撑和理论依据。

目前，针对电动汽车充电站实测负荷的相关研究还较为匮乏，成果少见。本文根据北京奥运快换式公交充电站历史观测负荷数据与运营数据，首先对快换站日负荷特征进行分析，研究影响快换站负荷变化的各类相关因素，主要包括日类型、气象因素与公交调度因素等；然后运用基于传递闭包法的模糊聚类分析来提取与待预测日影响因素相似的日期，组成相似日负荷样本作为神经网络的训练样本；最后建立BP网络对充电站日负荷曲线进行预测。实际算例表明，该方法应用于快换式公交充电站短期负荷预测是可行的。

1 快换式公交充电站负荷特征分析

1.1 概述

北京奥运充电站是一座大型快换式公交充电站，车辆进站后，快换机器人将车上电能消耗的电池组更换下来，接入充电平台开始为其补电，紧接着给车辆换上别组已经充满电的电池，而后车辆驶入特定区域，等待调度发车指令。根据公交调度收发车指令，每日上午七时以后出现回站充电车辆，充电站负荷开始上升，而当夜间最后一班车进站更换下来的电池组充电完毕后，充电机全部停机，充电站负荷降至最低。

图1是北京奥运公交充电站的一条典型日负荷曲线，图中横坐标为每日24点观测时刻，纵坐标为整点时刻的充电站有功功率。相比较传统电力日负荷曲线，公交快换站日负荷曲线同样具有较为明显的波峰波谷特征，但其曲线走向起伏波动较大，不同日负荷曲线之间差异性较高，全年日负荷曲线中，冬夏季负荷较高，春秋季负荷较低。这些都给充电站日负荷曲线的预测工作带来了较大的难度。

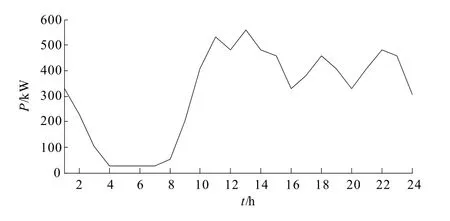
图1 北京奥运公交充电站典型日负荷曲线Fig. 1 Typical daily load curve of Beijing Olympic Games Bus Charging Station

快换式公交充电站之所以具有上述负荷特征，主要是因为站内负荷变化受到诸多因素的影响。通过对相关数据的研究分析，确立了主要以日类型、气象因素与公交调度因素等对快换式公交充电站日负荷曲线的影响。此外，交通拥堵状况和其他一些特殊情况所引起的突发事件也将对充电站负荷曲线造成影响，由于数据条件限制，文中对此暂不作讨论。

1.2 负荷影响因素

1.2.1 日类型

快换式公交充电站服务于城市电动公交车辆的电能补给工作，根据市民的日常生活习惯与乘坐需求，一周当中，公交车辆在工作日与周六日之间的调度安排有所不同，这也直接导致车辆充电负荷曲线在工作日与周六日之间出现了明显的差异性。

表1是北京奥运快换式公交充电站按星期类型做出的 2010年各日最高负荷全年均值和日平均负荷全年均值统计。从统计结果可以看出，全年工作日日最高负荷均值及日平均负荷均值明显与周六日不同，其中周一负荷值较高，其余工作日负荷较为相近，且周六日负荷也比较相近。因此，我们可以根据星期类型将一周划分为三种日类型，即周一为第一类，周二、周三、周四及周五为第二类，周六周日双休日为第三类。对于其他特殊节假日，诸如端午节、五一劳动节及国庆节等，可将其各自划分为单独的一类。

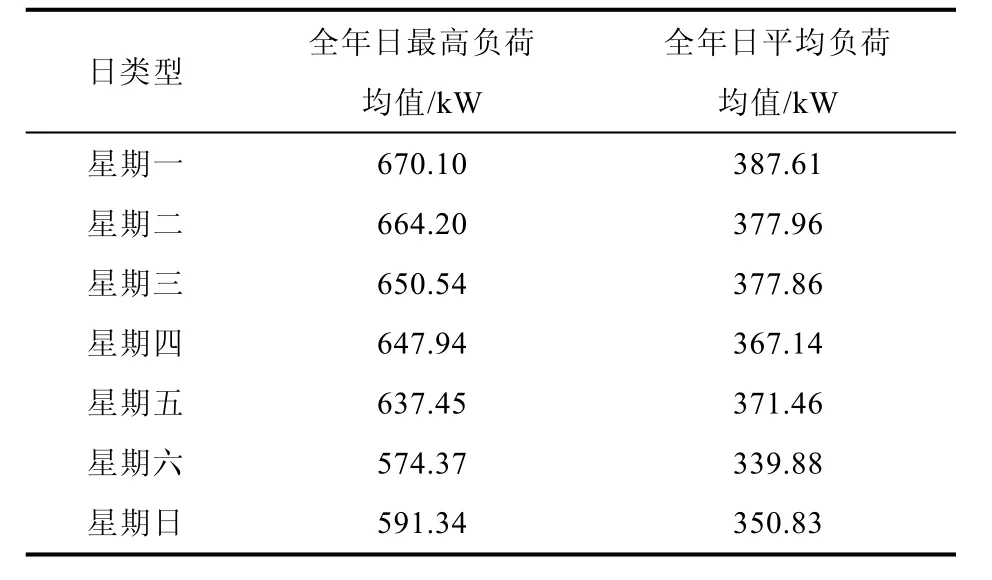
表1 不同星期类型负荷分析Table 1 Load analysis of different dates

1.2.2 气象因素

通过负荷数据与各类气象数据的相关性分析发现，快换式公交充电站负荷受气温的影响最为显著，而其他诸如湿度、风速等则影响微弱，可略去不计。据此，文章主要研究气温对充电站负荷的影响。类似于传统电力负荷，当气温冷暖变化加剧时，电动汽车由于车载空调的投入使用，车辆能耗增加，使得充电站日负荷曲线出现相应的增长。此外，由于气温对电动汽车动力电池的容量大小、充放电过程等有着重要影响，使得不同气温下电池组充电时长有所不同[7-8]，也会引起充电站负荷在不同气温下出现不同的变化趋势。

例如，相关数据显示，9月14日周二至16日周四连续三天充电车辆均为95辆左右，而最高气温却从35℃下降到24℃。从图2中可以看出，相邻几日气温的剧烈升降将会造成充电站日负荷曲线发生较大的改变，因此在后续相似日样本的选择中，有必要将气温作为特定的指标因素之一。

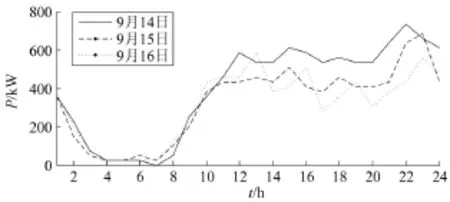
图2 温度变化与日负荷曲线变动关系Fig. 2 Relation between temperature variation and daily load curve

气温对充电站日负荷曲线的影响主要划分为日最高温度、日平均温度及日最低温度。图3是2010年各日日最高、日平均及日最低气温与充电站日最大负荷之间的关系曲线，可以看出，温度高低与负荷大小之间密切相关。此外观察发现，日最高、日平均及日最低温度与日最大负荷及日平均负荷均近似呈二次关系，并且关系曲线分别在20℃、15℃及10℃时出现拐点，这也为气温数据在后续规则化处理公式中a值的选择提供了依据。

图3 温度因素与日最高负荷关系曲线Fig. 3 Relation between temperature and daily maximum load

1.2.3 公交调度因素

收发车调度计划安排是公交运营公司的重要工作内容之一[9]，根据公交车辆每日的调度计划表，一天当中车辆回站充电的密集程度有所不同，致使充电站日负荷曲线在不同时段出现相应的升降变化。此外，根据工作日与节假日人们的乘坐需求不同、交通拥堵及突发状况时需要临时增发车来增强公交运力，致使不同日之间的公交车辆调度计划有所区别。公交调度因素是日负荷曲线出现波动起伏和不同日之间负荷曲线具有差异性的直接原因之一。根据公交运营公司提前和应急制定好的车辆调度计划表，可以估算得出待预测日需要充电的电动车辆总数，即日累计充电车辆数，以此作为公交调度因素对快换式公交充电站负荷的影响指标之一。

2 预测模型及算法

2.1 数据处理

电力负荷经过数据采集系统(SCADA)测量记录在数据库中。一方面，由于采集系统出现故障，负荷数据可能会出现伪信息、伪数值；另一方面，突发电力事故及负荷的突然投切，也会造成历史负荷数据的畸变[10]。为了防止异常负荷数据给模型预测带来不良影响，有必要对历史负荷数据进行补足修正。本文采用横向对比法修正异常负荷数据，在日负荷曲线中将t时刻负荷与其前后时刻负荷作横向对比，考虑电池组投切充电的时间间隔及负荷升降变化幅度，设立一定的阈值，当t时刻的负荷变化超过阈值时，取t时刻前后时刻的负荷平均值作为t时刻的实际负荷值。数据横向修正后确立待预测日，运用模糊聚类分析得到待预测日的相似日，考虑到相似日负荷样本的负荷曲线比较接近，为防止某日出现异常波动会干扰预测模型对正常负荷变化规律的认知，根据公式（1）将相似日样本每日t时刻负荷作纵向平滑处理。

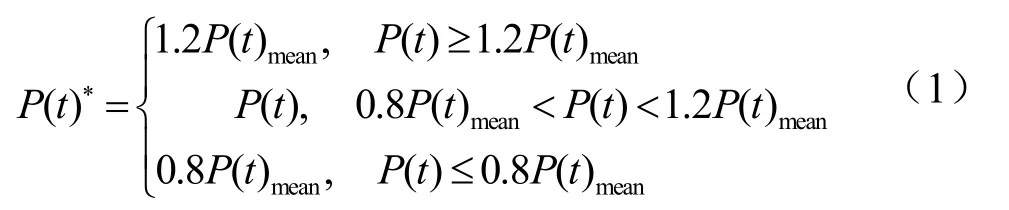
式中： P (t)为当日t时刻负荷值； P (t)mean为聚类后样本中各日t时刻的负荷平均值； P (t)∗为平滑后t时刻负荷值。

2.2 模糊聚类分析

模糊聚类是根据事物之间的属性特征，按一定要求和规律，将客观事物进行分类的数学方法[11]。考虑到充电站日负荷影响因素相似的日期之间负荷曲线基本一致，利用相似日负荷样本进行预测可以取得更好的预测效果[12]。本文选用模糊聚类分析中基于模糊等价关系的传递闭包法，为待预测日在其过往日期中客观提取出相似日样本，避免了凭人工经验选择相似日的盲目性，也克服了影响因素突变造成的非常规负荷数据给神经网络训练带来的不良影响。

前文中提到，影响快换式公交充电站负荷变化的主要因素有日类型、气象因素以及公交调度因素等，各日的这些影响因素构成当日一组特征向量为其中 xi1为日类型，xi2, xi3, xi4分别为日最高温度、日平均温度及日最低温度，xi5为日累计充电车辆数。假设待预测日及其待聚类的历史日期总共有n日，各日影响因素特征向量即组成统计指标样本集

式中ix为某日的一组影响因素特征向量。

依据统计指标样本集，模糊聚类分析具体步骤如下：

（1）数据规则化。由于各类影响因素数据的量纲与数量级不同，需要将其进行标准化处理，使之便于分析和比较。

对于日类型数据，根据不同日类型下负荷规律的不同，将日类型划分为五种，即周一、周二至周五、周六日及特殊节假日。用数字来表征负荷对不同日类型的不同响应，设定周一为0.9，周二至周五为1，周六为0.6，周日为0.5，特殊节假日为0。

对于气温数据，根据温度与负荷之间的变动关系，以式（2）对其进行规则化处理。

式中： f (t)为经规则化处理后的温度系数；t为各日相对应的温度；a为曲线折转点，日最高温度取20，日平均温度取15以及日最低温度取10。

对于公交调度因素即日累计充电车辆数，根据函数 n * = (n − nmin) /(nmax− nmin)对其进行规则化处理，式中n为各日累计充电车辆数， nmin和nmax分别为全年最小和最大日累计充电车辆数。

（2）标定与聚类。采用绝对值指数法，根据公式（3），计算模糊相似关系矩阵 R = (rij)。

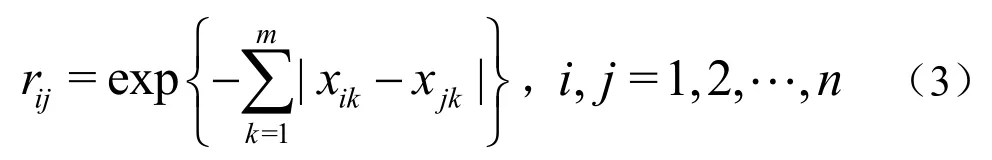
2.3 BP神经网络

神经网络因有强大的自学习和非线性函数逼近能力，使其在短期负荷预测中的应用尤为广泛[13]。本文采用基于误差反向传播算法的BP网络建立预测模型来对未来日负荷曲线进行预测。一个多输入单输出的三层BP网络结构如图4所示，包含输入层、隐含层及输出层。

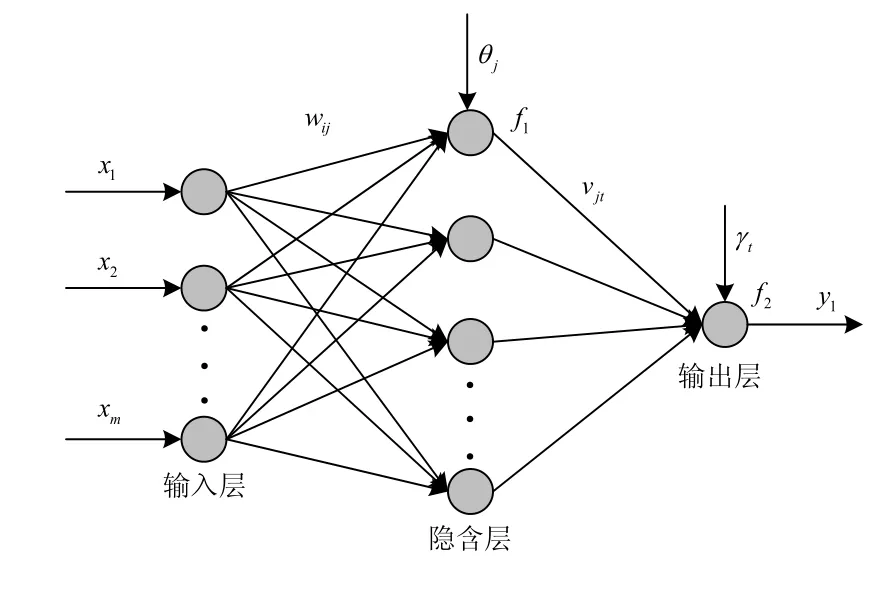
图4 三层BP神经网络结构图Fig. 4 Three-layer BP network

将经过模糊聚类分析提取出的相似日负荷数据作为BP网络的训练样本，考虑到网络的结构规模与学习效率，对每日24个时刻分别建立网络模型进行预测，最后形成一条完整的日负荷曲线。根据负荷“近大远小”的变化原则，在聚类后相似日样本中利用距离待预测日最近的相邻前三日的负荷来进行目标日负荷的预测，定义神经网路的输入输出如表2所示。

表2 BP神经网络输入输出定义表Table 2 Definition of inputs and outputs to BP neural network

基于Matlab神经网络工具箱[13]，网络的隐含层神经元传递函数选为双曲正切S型函数tansig，输出层神经元传递函数选为线性函数purelin。隐含层节点数参考文献[14]选为8个。为了提高网络的训练效率和泛化能力，采用贝叶斯正则化方法对网络进行学习训练。

3 预测实例分析

以北京奥运快换式公交充电站 2010年负荷数据及运营数据为依据，结合北京市当年各日的气象数据，运用上述预测方法，对充电站进行负荷预测实例分析。

为了消除目标日的特殊性，考察模型泛化性能，现选取5月31日作为春季测试日； 8月25日作为夏季测试日； 10月14日作为秋季测试日； 12月22日作为冬季测试日。预测后得到的日负荷曲线与实际日负荷曲线对比依次如图5~图8所示。

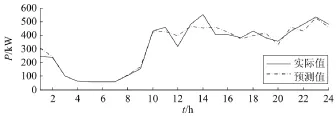
图5 春季测试日负荷实际值与预测值比较Fig. 5 Comparison of predicted value and actual value in spring testing

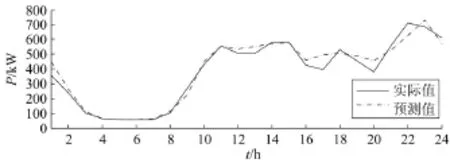
图6 夏季测试日负荷实际值与预测值比较Fig. 6 Comparison of predicted value and actual value in summer testing

图7 秋季测试日负荷实际值与预测值比较Fig. 7 Comparison of predicted value and actual value in autumn testing

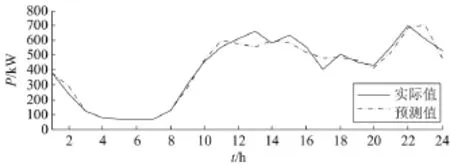
图8 冬季测试日负荷实际值与预测值比较Fig. 8 Comparison of predicted value and actual value in winter testing

为了与本文预测方法进行比较，建立单一 BP网络模型对与上文相同的四组测试日进行预测。单一BP网络模型的负荷训练样本未经过模糊聚类分析，只是简单选取待预测日前三周负荷来对目标日负荷进行预测。利用式（4）、式（5）计算预测误差和精度来衡量模型预测效果的好坏，两类预测模型统计对比如表3所示。

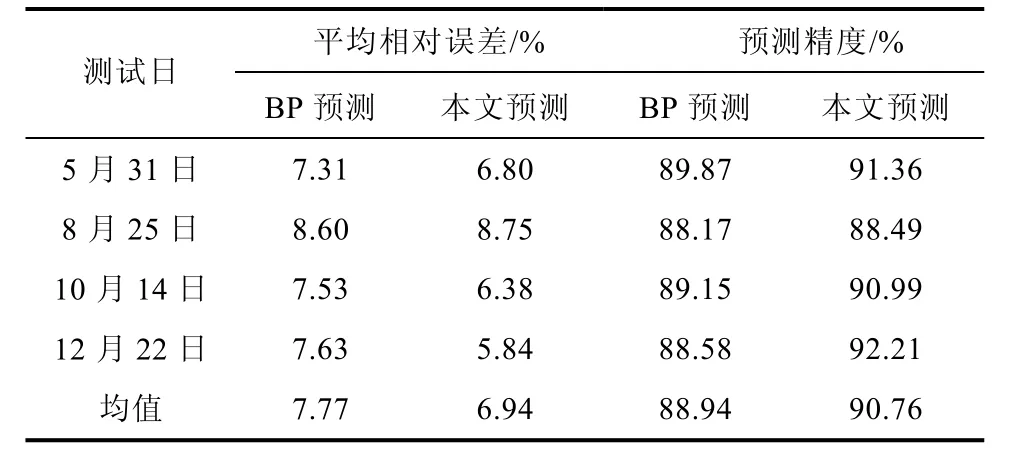
表3 预测误差与精度比较Table 3 Comparison of different forecasting methods

式中： εMAPE表示平均相对误差百分比；A是日负荷预测精度；Pt表示t时刻实际负荷值；表示t时刻预测负荷值；T表示日负荷曲线由T个负荷值组成，本文取24。

由表3可以看出，相比较于单一BP神经网络方法，模糊聚类分析与BP神经网络相结合的组合方法具有更好的预测效果，在四组测试日中，组合方法的整体预测误差比单一BP网络低了0.83个百分点，预测精度则高出1.82%。

由于快换式公交充电站负荷曲线波动大，周期性相似不明显，影响因素复杂、强耦合，使得其预测误差较大，精度也明显低于传统负荷预测。通过对组合方法进行多日测试，结果显示其平均相对误差百分比基本可以保持在10%以下，精度也大多维持在90%左右，满足一定的应用要求，是一种适用于快换式公交充电站短期负荷预测的方法。此外，观察日负荷曲线实际值与预测值可知，误差多出现于当日负荷值上下波动剧烈的位置，这与充电站电池组快速投切有关，在后续研究中，根据当日车辆调度的实时状态，有望提前修正这部分突变负荷所带来的误差。

4 结论

针对快换式公交充电站负荷特性，本文分析了影响快换站负荷变化的多种相关因素，运用模糊聚类分析提取出与待预测日影响因素相似的日期，这些日期的负荷作为相似日负荷样本带入BP神经网络进行学习训练，对待预测日负荷进行预测，最后与单一BP网络预测方法的预测结果进行对比分析。实际算例表明，该方法具有较高的预测精度，运用于快换式公交充电站的短期负荷预测是可行的。

快换式公交充电站负荷变化规律复杂，影响因素众多，是一种新兴的电力负荷。随着电动汽车的规模化应用，越来越多的快换式充电站开始投入使用，届时针对实际运行充电站的相关研究也将更加丰富。研究充电站负荷变化规律，分析充电站负荷与相关影响因子之间的内在联系，面向充电站自身的特有属性，寻求更加适宜于充电站的高精度负荷预测方法亦需要做出进一步的努力。

[1] 田立亭, 史双龙, 贾卓. 电动汽车充电功率需求的统计学建模方法[J]．电网技术, 2010, 34(11): 126-130．TIAN Li-ting, SHI Shuang-long, JIA Zhuo. A statistical model for charging power demand of electric vehicles[J]．Power System Technology, 2010, 34(11):126-130．

[2] 周逢权, 连湛伟, 王晓雷, 等. 电动汽车充电站运营模式探析[J]．电力系统保护与控制, 2010, 38(21): 63-66．ZHOU Feng-quan, LIAN Zhan-wei, WANG Xiao-lei, et al. Discussion on operation mode to the electric vehicle charging station[J]．Power System Protection and Control,2010, 38(21): 63-66．

[3] 李瑞生, 王晓雷, 周逢权, 等．灵巧潮流控制的电动汽车智能化充电站[J]．电力系统保护与控制, 2010,38(21): 87-90．LI Rui-sheng, WANG Xiao-lei, ZHOU Feng-quan, et al.The system of electric vehicle intelligence charge station with smart power flow control[J]. Power System Protection and Control, 2010, 38(21): 87-90.

[4] 廖旎焕, 胡智宏, 马莹莹, 等．电力系统短期负荷预测方法综述[J]. 电力系统保护与控制, 2011, 39(1)：147-148．LIAO Ni-huan, HU Zhi-hong, MA Ying-ying, et al.Review of the short-term load forecasting methods of electric power system[J]. Power System Protection and Control, 2011, 39(1): 147-148．

[5] 康重庆, 夏清, 刘梅．电力系统负荷预测[M]．北京：中国电力出版社, 2007．

[6] 牛东晓, 曹树华, 卢建昌, 等．电力负荷预测技术及其应用[M]. 北京: 中国电力出版社, 2009．

[7] 范美强, 廖维林, 吴伯荣, 等．电动车用 MH-Ni电池温度特性研究[J]．电池工业, 2004, 9(6): 287-289.FAN Mei-qiang, LIAO Wei-lin, WU Bo-rong, et al.Temperature characteristic of Ni-MH battery used in EVs[J]. Chinese Battery Industry, 2004, 9(6): 287-289．

[8] 张庆, 李革臣．锂离子电池充放电特性的研究[J]．自动化技术与应用, 2008, 27(12): 107-109．ZHANG Qing, LI Ge-chen. The charge/discharge characteristics of the Li-ion battery[J]. Techniques of Automation and Applications, 2008, 27(12): 107-109.

[9] 邹迎, 李建国, 杨忠伟．北京公交区域运营组织与调度系统初探[J]．城市公共交通, 2003(3): 15-18．ZOU Ying, LI Jan-guo, YANG Zhong-wei. Research on the regional operation organization and dispatch system of Beijing public transportation[J]. Urban Public Transport, 2003(3): 15-18.

[10] 陈亚红, 穆钢, 段方丽. 短期电力负荷预报中几种异常数据的处理[J]．东北电力学院学报, 2002, 22(2): 2-5．CHEN Ya-hong, MU Gang, DUAN Fang-li.Identification and management to anomalous data in short-term load forecasting[J]. Journal of Northeast China Institute of Electric Power Engineering, 2002, 22(2): 2-5．

[11] 李安贵, 张志宏 段凤英. 模糊数学及其应用[M]．北京：冶金工业出版社, 2000．

[12] 黎灿兵, 李晓辉, 赵瑞, 等. 电力短期负荷预测相似日选取算法[J]．电力系统自动化, 2008, 32(9): 69-73.LI Can-bing, LI Xiao-hui, ZHAO Rui, et al. A novel algorithm of selecting similar days for short-term power load forecasting[J]. Automation of Electric Power Systems, 2008, 32(9): 69-73.

[13] 葛哲学, 孙志强. 神经网络理论与 MATLABR2007实现[M]．北京：电子工业出版社, 2007.

[14] 高大启．有教师的线性基本函数前向三层神经网络结构研究[J]．计算机学报, 1998, 21(1): 80-86.GAO Da-qi．Research on structures of supervised linear basis function feed forward three-layered neural networks[J]. Chinese Journal of Computers, 1998, 21(1):80-86.