边坡层状岩体三维横观各向同性数值分析*

师文豪 杨天鸿 王培涛 于庆磊

(1.深部金属矿山安全开采教育部重点实验室;2.东北大学岩石破裂失稳研究中心;3.中国船舶重工集团公司第七二五研究所)

层状岩体是分布极其广泛的一种岩体类型，以我国的岩体为例，具有层状构造的沉积岩占到了77.3%［1］。研究层状岩体的损伤破坏规律对采矿工程至关重要。许多学者曾做过这方面的研究，但是大多都是理论解析解，如J.C.Jaeger等［2］做了大量且富有成效的理论和试验研究，为层状岩体力学行为和机制的进一步研究奠定了基础。一些学者对横观各向同性理论做了深入的研究，如乔世范等［3-5］针对沉积作用形成的岩体大多具有横观各向同性的特点，利用数学、力学手段，推导了横观各向同性地基应力－位移的理论解;张志增等［6-7］根据横观各向同性弹性力学的平衡方程、物理方程和几何方程，推导了二向不等压应力条件下横观各向同性岩体中深埋圆形巷道的位移解析解。M.E.Ghadi等［8］推导了由2个半空间构成的三维空间下的弹性动态解。从数值模拟的角度，对于层状岩体的特殊性质，杨天鸿等［9］提出了三维各向异性材料数值模型的计算方法，为分析层状岩体横观各向同性边坡的数值计算奠定了基础。本研究利用横观各向同性材料的相关理论知识，通过建立矿山边坡的三维连续介质数值计算模型，引入三维Hoffman强度准则，以此来研究层状岩体在不同倾角下的边坡破坏情况，为层状岩体边坡的设计、支护和监测提供借鉴意义。

1 三维横观各向同性的数值计算方法

由于层理结构面的存在，层状岩体具有明显的弹性各向异性和塑性各向异性，弹性各向异性体现在不同方向具有不同的刚度特性，而塑性各向异性体现在不同方向上具有不同的强度特性，鉴于此，将层状岩体简化为横观各向同性材料，来研究沿着层理面和垂直层理面的各向异性特征。

1.1 本构模型

为了建立模型，首先需建立空间三维坐标系，为了研究方便，在此建立2个坐标系统，即局部坐标系和整体坐标系。设平行层理面(即横观各向同性面)的坐标平面为x'oy'，垂直层理面的轴为z'轴，建立局部坐标系o－x'y'z'(即正轴坐标系)，3个坐标轴均在弹性主方向上;当横观各向同性面倾斜，即有一定倾角θ时，建立整体坐标系o－xyz(即偏轴坐标系)，3个坐标轴并非均在弹性方向上。如图1所示。

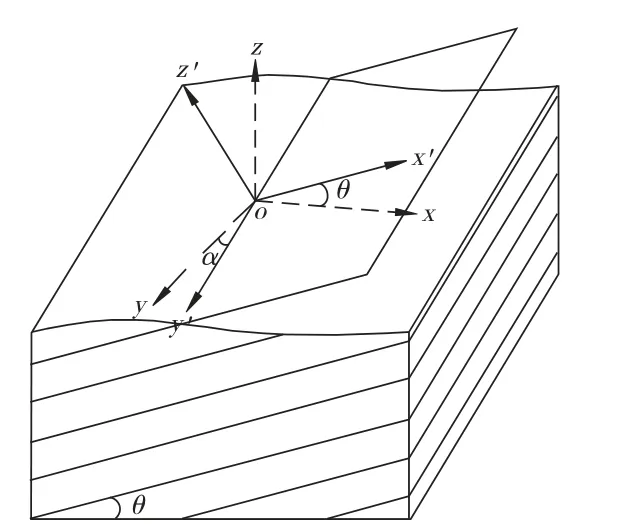
图1 正、偏轴坐标系中的横观各向同性模型

由横观各向同性理论知，局部坐标系下，材料的弹性应力－应变关系［10］为

式中，ε'为局部坐标系下的应变矩阵，σ'为局部坐标系下的应力矩阵，S'为局部坐标系下的柔度矩阵。

其中，E1、v1分别为横观各向同性方向的弹性模量和泊松比，E3、v3、G13分别为各向异性方向的弹性模量、泊松比和剪切模量。对于各向异性的剪切模量G13，Lekhnitskii［11］根据大量岩石的试验，建议采用式(3):

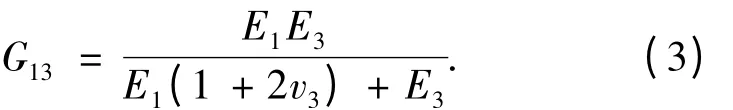
整体坐标系下，材料的弹性应力－应变关系为

式中，ε为整体坐标系下的应变矩阵，σ为整体坐标系下的应力矩阵，S为整体坐标系下的柔度矩阵。

根据坐标变换关系可知

式中，Q为转换矩阵，li、mi、ni(i=1，2，3)分别为2坐标轴之间夹角的余弦，其对应关系如表1所列。

表1 整体、局部坐标系之间的关系

1.2 各向异性屈服准则

大量的试验研究和工程实践认为，层状岩体具有复杂的破坏模式，如复合型破坏。对于层状岩体，岩层轴向和各向同性面的抗拉、抗压强度明显不同，经典Mohr－Coulomb强度准则不再适用，本研究充分考虑材料3个正交主方向上的抗拉、抗压强度与3个主平面内的抗剪强度来描述材料的各向异性强度特征，把三维Hoffman各向异性屈服准则引入到层状边坡稳定性分析中，三维Hoffman各向异性屈服准则［12］可表示如下:

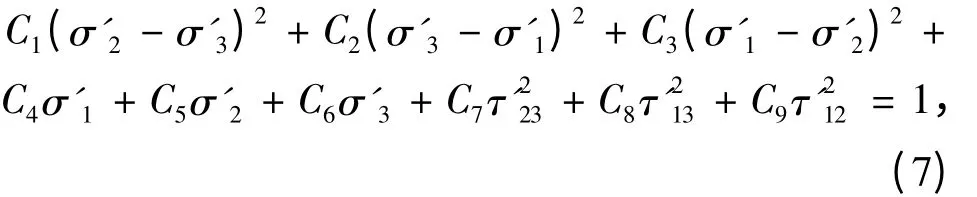
式中C1，C2，…，C9为各向异性强度系数，由3个弹性主方向的抗压强度Xc、Yc、Zc，抗拉强度Xt、Yt、Zt和3个主平面内的剪切强度S12、S23、S13决定，各个强度系数表达式为

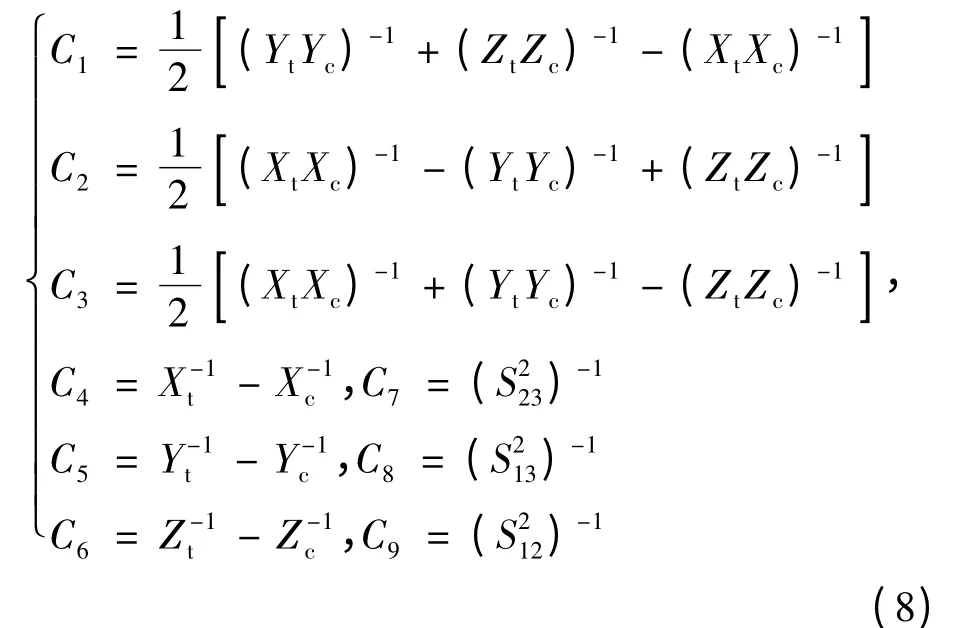
对于横观各向同性材料，有Xc=Yc，Xt=Yt，S13=S23。另外，式(7)中σ'1，σ'2，σ'3，τ'12，τ'13，τ'23为局部坐标系下的应力分量，可通过对整体坐标系下的应力分量进行坐标转换求得，坐标转换关系为

2 模型计算与样例分析

以某矿山边坡为例，建立如图2所示的三维边坡数值分析模型。整体模型尺寸为1 500 m×1 000 m×400 m。对模型施加一定的边界条件:底部固定，四周约束水平位移，允许自由沉降，模型中只考虑岩体自重(密度ρ=2 700 kg/m3)的影响，通过自重产生水平地应力，以此来模拟实际矿山边坡的应力场分布。层状岩体各向异性变形参数和强度参数根据巫德斌［13］和Bona Park等［14］的研究成果进行估算取值，模型计算中采用的岩体物理力学参数如表2所列，参数的合理性需要开展工程原位试验进一步验证。

图2 三维边坡数值分析模型

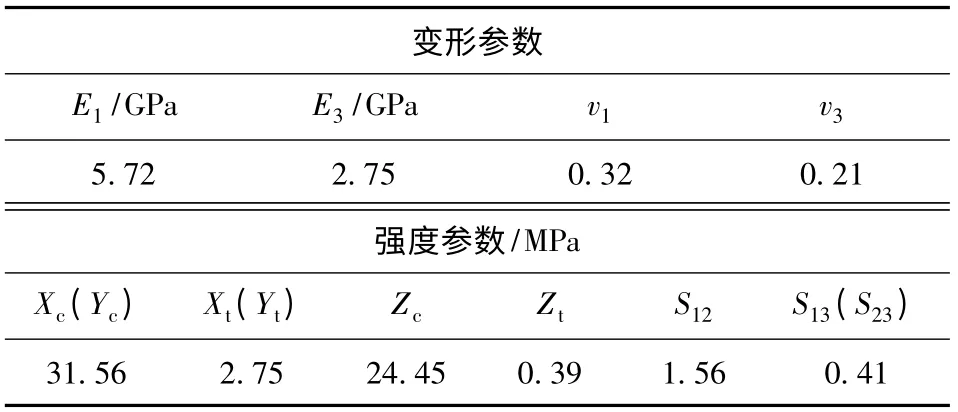
表2 岩体的物理力学参数

利用COMSOL Multiphysics有限元分析软件对模型进行数值计算，设θ为各向同性面与X轴正方向的夹角，在工程地质中，θ可以通过地层倾角测井仪测试得到。当岩层与x轴正方向夹角θ=0°时，各向同性面为xoy平面，当θ≠0°时，各向同性面为xoy平面绕y轴逆时针旋转θ角所成的平面，如图3所示。依据不规则边界局部细化，规则边界粗化的原则，对模型进行网格划分，共划分21 612个网格单元，总计107 283个自由度数量。

图3 各向同性面方向示意

随着θ角的不断变化，岩体在层面方向和层面法线方向表现出明显的各向异性特征，为了研究的方便，取图4所示位置截面进行分析。图5、图6分别为该截面在不同θ值下的主应力和剪应力云图。

图4 截面在边坡中位置

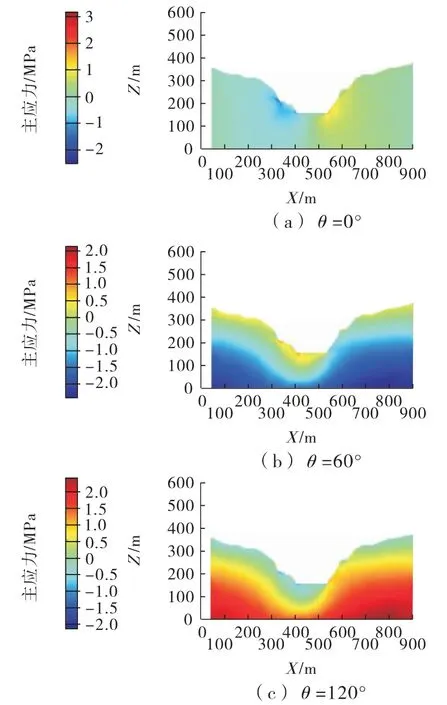
图5 不同θ值下主应力云图

从图5、图6中可以很直观地看出，由于层理结构面的存在，使得层状岩体的变形参数在各向同性面内和各向异性面内存在一定差异，各向异性面内岩体更容易产生变形，从而导致层状岩体的力学性能在全局坐标系下表现出明显的方向性。即沿着层理面和垂直层理面方向的岩体力学性质有较大差异，随着θ值的不断变化，层状岩体的主应力和剪应力均发生变化，且变化趋势保持一致，因此也表明了层理结构面的产状对层状岩体的岩体力学性质起着控制作用，从而对此类岩体边坡的稳定性起着决定性作用。边坡坑底正下方10 m位置(如图7中AA'线所示)的主应力和剪应力变化曲线如图8、图9所示。除了θ=0°和90°外，由于其他角度层状岩体的非对称性，主应力曲线也均不是对称曲线，如图8所示;对于层状岩体，边坡开挖形成后一侧帮边坡为顺倾岩层，另一侧帮边坡则为反倾岩层，在岩体自重作用下，两侧帮边坡岩体的剪应力的方向将截然相反，因此剪应力曲线存在一定的反对称性，如图9所示。

图6 不同θ值下剪应力云图

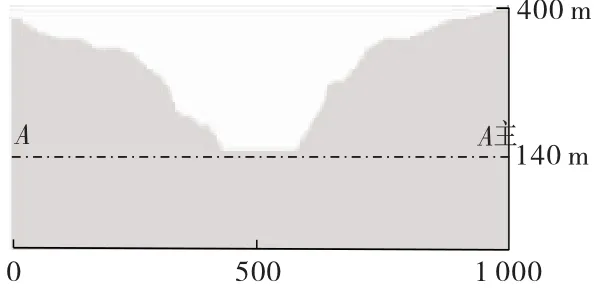
图7 边坡正下方10 m(A－A')位置

图8 A－A'位置主应力曲线

根据三维Hoffman准则，引入损伤变量d z，

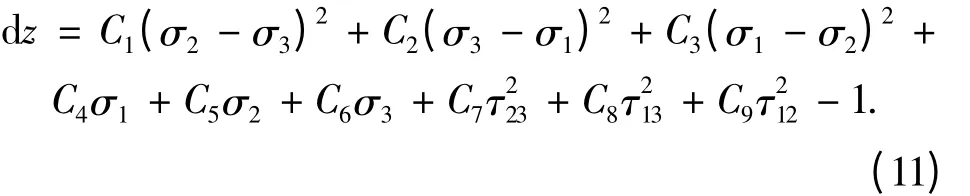
当d z＞0，则认为材料发生损伤破坏。

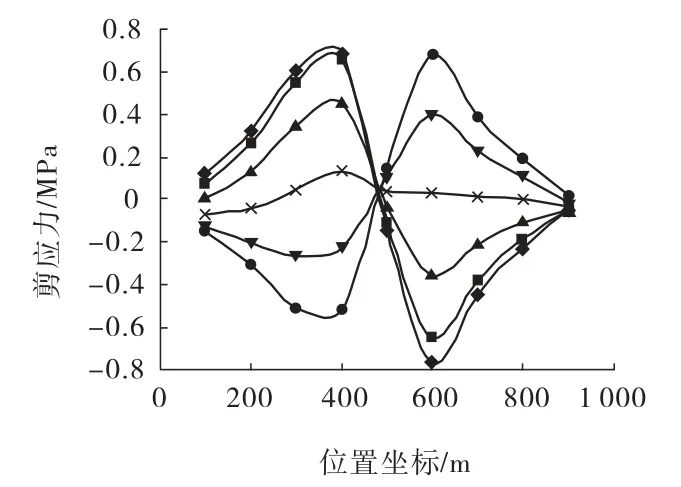
图9 A－A'位置剪应力曲线

随着θ值的不断变化，不同方位的损伤区变化非常明显，说明岩层倾角对边坡的稳定性影响很大，图10给出了不同θ值下的损伤区分布。从图10中可以看出当θ=0°，即岩层为水平分布时，损伤主要发生在坑底及两侧帮边坡;当θ=90°，即岩层为竖直分布时，损伤主要发生在两侧帮，在坑底没有损伤出现。结合图9、图10可知，θ=0°时的剪应力明显大于θ=90°时的剪应力，而θ=0°时的主应力却小于θ=90°时的主应力。θ=0°时，岩层为水平分布，坑底及侧帮边坡的剪应力占主导地位，导致岩层出现层间剪切滑移趋势，由于层间节理面的存在使得其抗剪强度较差，因此在剪应力作用下发生以剪切为主的损伤破坏;而θ=90°时，岩层为竖直分布，两侧帮边坡的主应力占主导地位，导致岩层呈现倾倒趋势，由于竖直层理面的存在，边坡在水平方向的抗拉强度较差，因此在主应力作用下发生以拉应力为主的倾倒破坏。当θ=60°，岩层为倾斜分布，在主应力和剪应力共同作用下岩体发生拉剪组合破坏。θ在0°～90°变化时，岩层从剪应力为主的破坏到拉剪组合破坏再到以拉应力为主的破坏过渡。

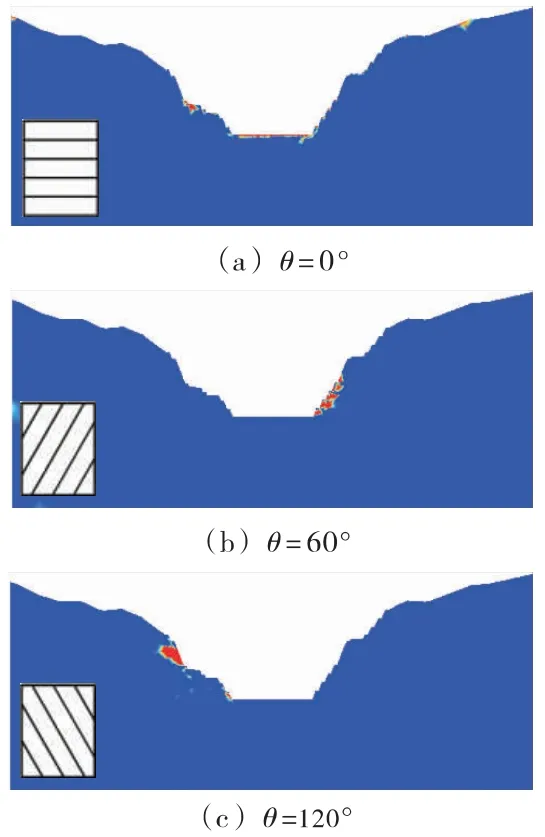
图10 不同θ值下损伤区

三维模型在不同θ值下损伤区变化:当各向同性面水平或竖直(即θ=0°或θ=90°)时，边坡两侧帮的损伤区分布较为均匀;当0°＜θ＜90°时，由于模型右帮边坡的岩层相对边坡为顺倾，岩层较容易发生剪切滑移型破坏，所以损伤区主要集中在右帮边坡，且不同角度时损伤区大小及损伤位置均有所差异，而左帮边坡岩层为反倾，仅出现局部小范围损伤，整体不易发生剪切滑移破坏，相对较稳定;同理，当90°＜θ＜180°时，由于模型右帮边坡的岩层相对边坡为顺倾，所以这个范围内的损伤区主要集中在边坡左帮，右帮边坡岩层为反倾，仅出现局部小范围损伤，整体不易发生剪切滑移破坏，相对较稳定。

3 结论

(1)提出了层状岩体的三维横观各向同性计算方法，并且引入了三维Hoffman各向异性强度准则，模拟了不同岩层倾角情况下的边坡破坏模式。当θ=0°，即岩层为水平分布时，损伤主要发生在坑底及两侧帮边坡，在剪应力作用下易发生以剪切为主的损伤破坏;当θ=90°，即岩层为竖直分布时，损伤主要发生在两侧板，在坑底没有损伤出现，主应力作用下易发生以拉应力为主的倾倒破坏;θ在0～90°变化时，岩层从剪应力为主的破坏到拉剪组合破坏再到以拉应力为主的破坏过渡。

(2)对于层状岩体边坡而言，顺倾岩层的边坡更容易发生整体性的剪切滑移型破坏，而反倾岩层的边坡整体不易发生剪切滑移破坏，大多存在局部小范围损伤，整体相对较稳定。

［1］ 艾智勇，成怡冲.三维横观各向同性成层地基的传递矩阵解［J］.岩土力学，2010，31(2):25-30.

［2］ Jaeger JC，Cook N G W.岩石力学基础［M］.3版.中国科学院工程力学研究所，译.北京:科学出版社，1981:582-600.

［3］ 乔世范，顿志林，刘宝琛.水平荷载作用下横观各向同性地基力学性态研究［J］.岩石力学与工程学报，2004，23(7):1212-1218.

［4］ 乔世范，顿志林，刘宝琛.横观各向同性地基模型的理论分析及其应用［J］.岩土工程技术，2003(4):213-219.

［5］ 乔世范，顿志林.横观各向同性地基本构模型研究［J］.力学与实践，2005，27:50-53.

［6］ 张志增，李仲奎.横观各向同性岩体中圆形巷道反分析的惟一性［J］.岩土力学，2011，32(7):2066-2072.

［7］ 张志增，李仲奎，许梦国.横观各向同性岩体中深埋圆形巷道的位移解析解［J］.黄金，2010，31(3):23-26.

［8］ Ghadi M E，Sture S，Pak R.Y.S，et al.A tri-material elastodynamic solution for a transversely isotropic full-space［J］.Int Jof Solids and Structures，2009，46:1121-1133.

［9］ 杨天鸿，黄龙现，王培涛，等.三维各向异性材料数值模型的计算方法［J］.东北大学学报:自然科学版，2012，33(10):1479-1483.

［10］ 沈观林，胡更正.复合材料力学［M］.1版.北京:清华大学出版社，2006:29-41.

［11］ Lekhnitskii SG.Theory of Elasticity of an Anisotropic Body［M］.Moscow:Mir Publishers，1981:130-145.

［12］ 陈火红，于军泉，席源山.MSC.Marc/Mentat 2003基础与应用实例［M］.北京:科学出版社，2004:232-242.

［13］ 巫德斌.层状岩体边坡工程力学参数研究［D］.南京:河海大学，2004.

［14］ Bona Park，Ki-Bok Min.Discrete element modeling of shale as a transversely isotropic rock［C］∥2012 ARMS7-7th Asian Rock Mechanics Symposium.Seoul:Korean Society for Rock Mechanics，2012:336-342.