贝叶斯算法在拟合自由核章动参数中的应用

崔小明，孙和平，S Rosat，徐建桥，周江存，陈晓东

1 中国科学院测量与地球物理研究所 大地测量与地球动力学国家重点实验室，武汉 430077

2 中国科学院大学，北京 100049

3 Institut de Physique du Globe de Strasbourg，Strasbourg 67084

1 引 言

自由核章动是由于液核和地幔的转动瞬轴错位，在具有微小椭率的核幔边界（CMB）上产生内部压力和压力矩，从而导致旋转椭球地球产生除Chandler摆动之外的又一地球自转简正模，由于该简正模在地固系中的本征周期接近1恒星日，故称为近周日自由摆动（NDFW），在惯性空间表现为自由核章动［1］.

自由核章动现象会引起核幔边界，整个地幔乃至地球表面的微小形变和引力位的扰动，在地球重力固体潮周日潮波中，引起与NDFW频率接近项出现明显的共振放大现象.目前根据重力固体潮共振现象拟合FCN参数的方法主要为传统最小二乘法，由于FCN信号微小，其在重力固体潮观测中引起的共振效应的某些潮波振幅小，观测信噪比低，这极大地影响了最小二乘法拟合FCN参数的精确度，而FCN周期和品质因子参数分别与CMB动力学椭率和CMB黏滞系数、电导率等与耗散有关的物理参数密切相关，是地球内部尤其CMB研究的重要约束，因此FCN参数拟合方法的改进对于重力技术约束地球深内部物理性质具有重要意义［2］.

由于最小二乘法是一个寻找最优解的过程，数据中含有的误差或噪音会影响最小二乘的解.国际同行曾将贝叶斯算法［3－4］引入到FCN参数的拟合中进行了实验.贝叶斯算法是在先验信息的背景下，充分利用观测数据，缩小待求参数的分布范围，获得这些参数的后验概率密度分布，揭示参数值的最可能分布，同时结果反映了待求参数的不确定性.

为详细研究贝叶斯算法在提高重力资料拟合FCN参数精度方面的有效性.本文根据武汉台站观测的超导重力资料和全球地球动力学合作观测研究计划（GGP）提供的全球其他台站的资料基于贝叶斯方法来研究FCN参数，同时探讨了影响FCN参数拟合的几个重要因素.

2 贝叶斯算法

FCN参数的计算模型为基于周日潮波（如P1、K1、ψ1、φ1波等）观测中出现的共振放大现象随频率σ变化的重力振幅因子共振模型［5］：

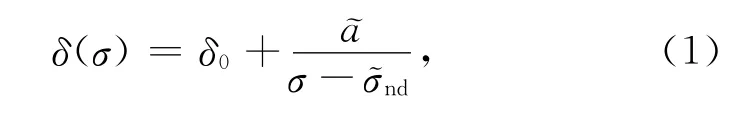
式中δ0是振幅因子中与频率无关且不受FCN共振影响的部分，本文取δ0＝）／2，为 O1和OO1波重力振幅因子实部的均值；～a为依赖于地球形状和地幔介质流变特征的复共振强度，～σnd称为复本征频率.记.模型中引入x＝lgQ为先验信息（Q为FCN品质因子）保证Q为正值，模型实部虚部展开为：

贝叶斯算法是以先验信息和观测数据为基础，获取待求参数的后验概率密度分布［6］：

由公式（1）—（3）建立的贝叶斯算法拟合FCN参数的后验概率密度表达式为［4］：

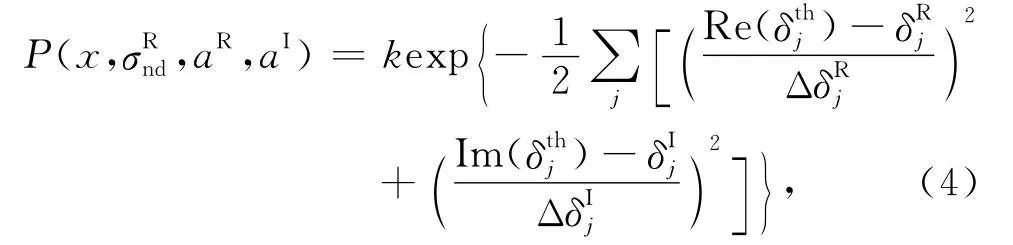
3 实例分析

武汉超导重力台站是基于中国科学院测量与地球物理研究所武汉九峰动力大地测量学观测站于1997年11月安装GWR－C032超导重力仪建立的，参加了国际大地测量和地球物理联合会（IUGG）下属的地球深部研究小组于1997年组织实施的全球地球动力学合作计划在全球部署的超导重力仪台站网 络［7－8］；本文使用的其他22个台站分别为欧洲11个，亚洲5个，美洲3个，非洲1个，大洋洲1个，南极1个.所有超导观测资料经统一预处理软件T－soft修正数据中的阶跃、尖峰、掉格和地震等干扰信号［9］；并采用统一分析软件（Eterna）调和分析各台站的重力潮汐观测数据，获得重力因子、相位滞后等潮汐参数［10－11］.Eterna调和分析过程中通过引入大气重力导纳值将混合在观测资料中的大气压力变化信号消除，获得经气压改正后的高精度重力潮汐常数，之后通过海潮模型来改正海潮的影响［12］.

根据第二节介绍的贝叶斯算法，利用全球超导重力台站的资料拟合了FCN的本征周期和品质因子等参数.考虑到不同台站观测资料本身质量受海潮及区域背景噪音及其他因素导致的影响程度不同，调和分析后获得的潮波（P1、K1、ψ1、φ1波）振幅因子及相位精度亦不同，如欧洲台站受海潮影响小，普遍比较稳定，测定的潮波振幅因子和相位精度较高，资料质量较好；相比而言，其他地区台站尤其亚洲和南半球台站受诸多因素（主要是海潮）影响较大，潮波振幅因子和相位测定精度较低，资料质量较差.图1和图2分别列出了Moxa（德国）台站和武汉站的拟合结果为例，这两个台站的结果基本反映了资料质量不同的超导重力数据拟合FCN参数的特点.其中Moxa资料长度为2001年月1日—2010年4月31日，武汉站为1997年12月21日—2004年12月19日.两图中左侧为拟合参数的联合概率密度分布，反映了参数间的相关性程度，倾斜形状越大，参数间相关性越高，参数的高相关性会使拟合的不确定性增大，影响拟合精度，所以联合概率密度分布图直观地反映了超导重力各台站资料拟合FCN参数的优劣，可以作为衡量超导重力资料研究FCN参数的参考标准；右侧为FCN周期和品质因子的概率密度分布，中间虚线为最小二乘法拟合的相应参数值.对Moxa台站，最小二乘法的周期和品质因子结果分别为428.3（天）和10072，贝叶斯算法的结果为428.1（天）和13069；对武汉台站，最小二乘法的周期和品质因子结果分别为426.0（天）和5081，贝叶斯算法的结果为433.1（天）和23081.

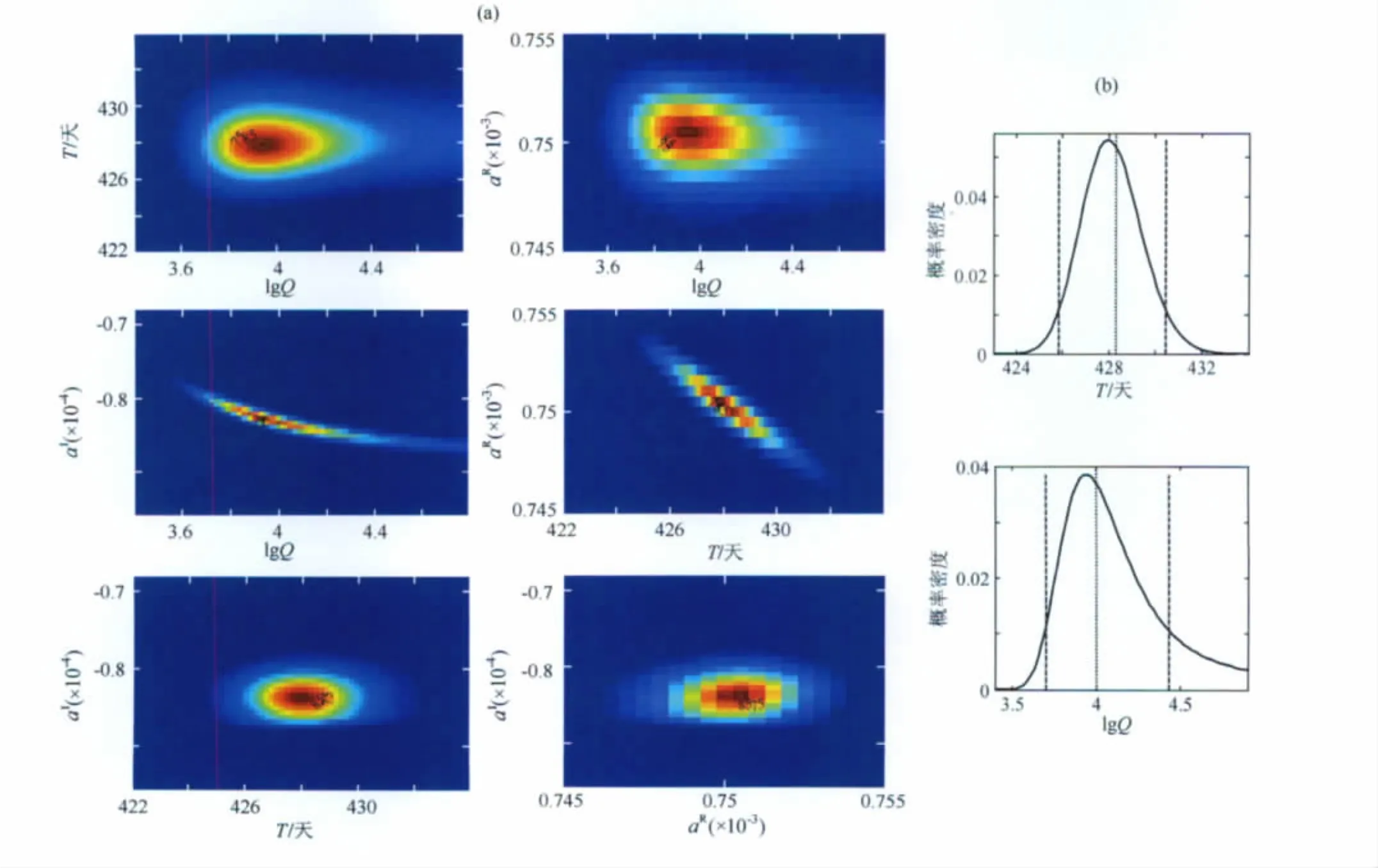
图1 Moxa台站资料拟合的FCN参数（a）参数联合概率密度分布；（b）周期T和品质因子Q概率密度分布.Fig.1 FCN parameters fitted from observations in Moxa station（a）Joint pdfs for FCN parameters；（b）Marginal pdfs for period ＆quality factors.

图2 武汉台站资料拟合的FCN参数（a）参数联合概率密度分布；（b）周期T和品质因子Q概率密度分布.Fig.2 FCN parameters fitted from observations in Wuhan station（a）Joint pdfs for FCN parameters；（b）Marginal pdfs for period ＆quality factors.

对于图1资料质量高的台站（Moxa），左侧联合概率密度分布图中上下四幅图基本呈圆形，中间两幅仍然会呈狭长形状，说明共振强度虚部（aI）与品质因子，实部（aR）与周期存在较高相关性.右侧图中，对于Moxa台站来说，FCN周期参数基本服从正态分布，两种方法从超导重力资料中拟合的周期非常一致；而品质因子的概率密度则偏离正态分布，这主要是由于个别潮波信噪比小导致的潮波相位测定偏差所致.此时最小二乘的结果仍然基本是最大概率密度处的参数值，与贝叶斯算法给出的90%置信区间内品质因子参数的平均值不符，此处贝叶斯算法给出的品质因子结果绝对值要高于最小二乘法结果，更接近空间大地测量技术VLBI章动观测资料的拟合结果.表1列出了VLBI资料拟合FCN参数的结果，由于FCN引起共振效应的受迫章动项振幅较大，信噪比高，其参数拟合结果相比于重力资料精度要高，可以作为我们测试贝叶斯方法的有效参考.

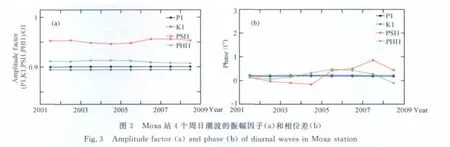
图2为武汉站的结果，从参数的联合概率密度分布来看，几乎都较大偏离了圆形，即各个参数之间存在高相关性，反映了该台站资料拟合结果的不确定性程度较高，说明武汉台站超导重力资料存在问题.武汉站总资料长度为1997年12月至2011年4月，由于调和分析ψ1、φ1波的精度不够高，在计算FCN参数去掉了2005年之后的数据.我们以三年时间间隔，1年重叠，对武汉和Moxa台站分段调和分析得到了不同时段P1，K1，ψ1（PSI1）和φ1（PHI1）波的振幅因子和相位差，列于图3和图4中.图中结果非常清晰地反映了两个台站资料得到的周日潮波尤其是ψ1（PSI1）和φ1（PHI1）波的差异，Moxa站获得的这两个潮波的振幅因子非常稳定，相位差有一定的变化但变化幅度非常小（＜1°），武汉站的结果无论振幅（尤其2004年之后）还是相位差（变化幅度＞10°）都非常不稳定，海潮、大气、台站区域性噪音以及台站仪器没有精确标定响应滞后，都是可能的影响因素.从参数的概率密度分布来看，较大的背景噪音及相位系统偏差等因素造成了FCN周期和品质因子都偏离了正态分布，贝叶斯算法和最小二乘法得到的周期及品质因子结果都不一致，此时，贝叶斯算法拟合的FCN参数（尤其品质因子）与传统最小二乘相比具有明显的优势，其结果更接近于VLBI资料拟合的结果.

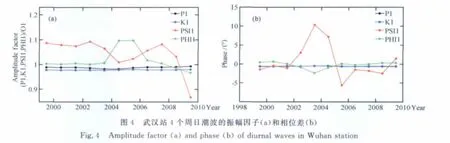
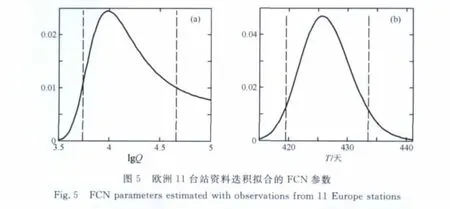
对于全球其他台站资料来说，资料质量较高（即潮波振幅及相位测定精度高）的台站结果与Moxa类似，仅品质因子偏离正态分布，这些台站基本集中在欧洲，考虑到充分利用超导重力仪多台站分布的特点，迭积多个台站资料一直是消除资料中部分区域性噪音影响的有效手段［16］.我们在图5中列出了数据质量较好的欧洲11个台站（包括Homburg，Brussels，Medecina，Membach，Metsahovi，Moxa，NY－Alesund，Potsdam，Strasbourg，Vienna，Wettzell）的数据序列根据贝叶斯算法迭积计算的FCN参数，周期和品质因子在置信区间的均值为426.5（天）和17116.迭积多个台站的观测资料获得的品质因子结果相比单个台站（Moxa）更接近于VLBI结果，表明迭积处理方式的有效性进一步改善了重力资料研究FCN的结果.而资料质量相对差一些的台站主要为亚洲和南半球的台站，由于受海潮或台站周边噪音影响较大，结果类似武汉台站，周期和品质因子都偏离正态分布.

上述分析中已经提到贝叶斯和最小二乘方法的选择对资料质量高的台站资料获得的FCN周期结果并无多大影响，下面简单讨论了超导重力资料拟合FCN参数过程中潮波的选择以及海潮模型对周期拟合的影响.

表2利用欧洲Medicina台站的重力数据对比了通常使用的P1、K1、ψ1、φ1四个潮波和Rosat等［4］中使用的九个潮波（包括 Q1，O1，M1，P1，K1，ψ1，φ1，J1和OO1）的贝叶斯算法计算结果，结果表明潮波数对FCN周期结果的影响达到几天，对品质因子的影响不显著，而通过对其他台站的研究发现，该影响的大小并不固定.所以如何评定潮波的选择以及选择哪些潮波合适是我们在使用重力资料研究FCN时需要考虑的重要因素.

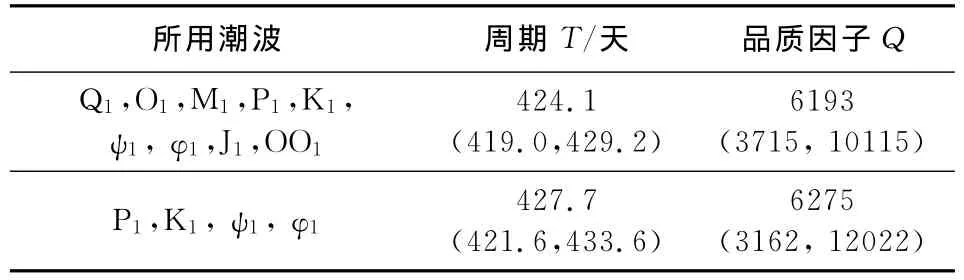
表2 欧洲Medicina台站不同潮波数FCN拟合结果Table 2 FCN results of different waves fitted from observations in Medicina stations

海潮模型也是影响FCN参数拟合的重要因素，表3列出了欧洲Strasbourg台站利用不同海潮模型改正后的重力振幅因子拟合的FCN参数结果.由结果可以看出，海潮模型对FCN周期和品质因子的影响都非常明显，对周期的影响达到几天，对品质因子的影响达数千量级.此外，对全球多个台站的研究显示不同海潮模型对FCN参数的影响具有明显区域性，对于欧洲台站，Fes02和Fes04海潮模型对应的周期偏大，而对于其他地区的台站如南非Sutherland台站，Fes02和Fes04海潮模型对应的周期相比其他模型偏小.然而由于不同海潮模型对不同地区台站的影响并不呈非常一致的系统性，其区域性效应与构建模型的资料相关［17－18］，因此对于不同海潮模型的区域性影响以及如何选择合适的海潮负荷改正是需要进一步研究的重要内容.

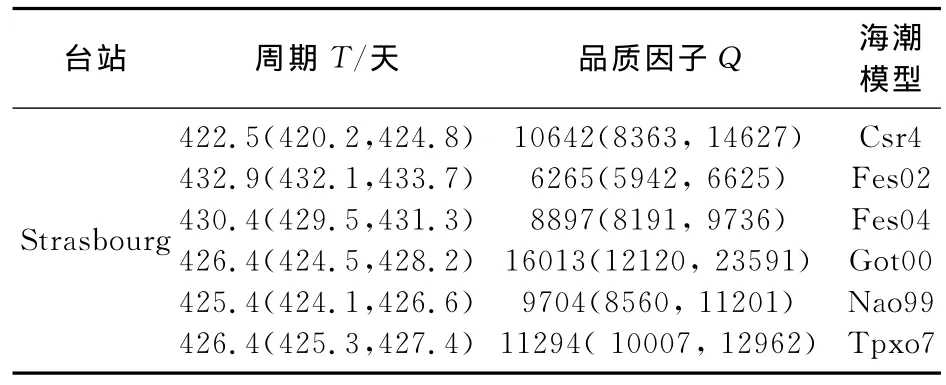
表3 Strasbourg不同海潮模型对FCN拟合结果的影响Table 3 FCN results fitted from observations in Strasbourg station and different ocean tidal models

4 结 论

利用武汉国际潮汐基准站高精度超导重力仪和全球超导重力仪观测的时变重力资料，根据贝叶斯算法拟合了FCN周期和品质因子等参数，结果验证了贝叶斯方法对于改进重力资料拟合FCN参数的有效性，对于潮波振幅及相位测定精度高的台站，贝叶斯算法和最小二乘法对周期的拟合结果基本一致；对于品质因子，贝叶斯算法与传统最小二乘相比具有明显的优势，其拟合结果更接近精度更高的VLBI资料的结果，体现了其充分利用先验信息和观测数据提高参数拟合精度的优越性，获得的结果更加可靠.除计算方法外，在FCN参数拟合过程中，选择不同的周日潮波或使用不同海潮模型进行海潮负荷改正也会对拟合结果有显著影响.

（References）

［1］徐建桥，许厚泽，孙和平等.利用超导重力仪观测资料检测地球近周日共振.地球物理学报，1999，42（5）：599－608.Xu J Q，Xu H Z，Sun H P，et al.Investigation of the Earth′s nearly diurnal free wobble resonance using tidal gravity observations with superconducting gravimeters.Chinese J.Geophys.（in Chinese），1999，42（5）：599－608.

［2］孙和平，崔小明，徐建桥等.超导重力技术在探讨核幔边界粘性特征中的初步应用.地球物理学报，2009，52（3）：637－645.Sun H P，Cui X M，Xu J Q，et al.Preliminary application of superconductive gravity technique on the investigation of viscosity at core－mantle boundary.Chinese J.Geophysics.（in Chinese），2009，52（3）：637－645.

［3］Florsch N，Hinderer J.Bayesian estimation of the free core nutation parameters from the analysis of precise tidal gravity data.Physics of the Earth and Planetary Interiors，2000，117（1－4）：21－35.

［4］Rosat S，Florsch N，Hinderer J，et al.Estimation of the Free Core Nutation parameters from SG data：Sensitivity study and comparative analysis using linearized least－squares and Bayesian methods.Journal of Geodynamics，2009，48（3－5）：331－339.

［5］徐建桥，孙和平，罗少聪.利用国际超导重力仪观测资料研究地球自由核章动.中国科学 （D辑），2001，31（9）：719－726.Xu J Q，Sun H P，Luo S C.Study of the Earth′s free core nutation by tidal gravity data recorded with international superconducting gravimeters.Science in China （Series D），2002，45（4）：337－347.

［6］Tarantola A，Valette B.Inverse problems＝ Quest for information.J.Geophys.1982，50：159－170.

［7］徐建桥，孙和平.武汉超导重力仪测定的近周日共振.自然科学进展，2002，12（1）：70－73.Xu J Q，Sun H P.Nearly diurnal resonance measured with a superconducting gravimeter at Wuhan.Progress in Natural Science （in Chinese），2002，12（1）：70－73.

［8］Crossley D J，Hinderer J.Global geodynamics project－GGP：status report 1994.／／Poitevin C.ed.Proceedings of the Workshop on Non－tidal Gravity Changes.Luxembourg：Conseil de L′Europe Cahiers du Centre Européen de Géodynamique et de Séismologie，1995，11：244－269.

［9］Vauterin P.Tsoft：Graphical and interactive software for the analysis of Earth tide data.／／Ducarme B，Paquet P，eds.Proceedings of the 13th International Symposium on Earth Tides.Brussels：Série Géophysique，1998：481－486.

［10］Tamura Y.A harmonic development of the tidal generating potential.Bulletin d′Information de Marees Terrestres，1981，64：677－704.

［11］Wenzel H G.The Nanogal Software：Earth tide data processing package ETERNA3.30.Bulletind′Information deMareesTerrestres，1996，124：9425－9439.

［12］孙和平，罗少聪.地球物理场观测中的大气效应问题研究.地球物理学进展，2002，17（3）：507－513，472.Sun H P，Luo S C.Study of the atmospheric pressure influence on geophysical observations.Progress in Geophysics （in Chinese），2002，17（3）：507－513，472.

［13］Mathews P M，Herring T A，Buffett B A.Modeling of nutation and precession：New nutation series for nonrigid Earth and insights into the Earth′s interior.J.Geophys.Res.，2002，107（B4）：2068，doi：10.1029／2001JB000390.

［14］Vondrak J，Ron C.Stability of period and quality factor of free core nutation.Acta Geodyn.Geomater.，2009，6（3）：217－224.

［15］Rosat S，Lambert S B.Free core nutation resonance parameters from VLBI and superconducting gravimeter data.A ＆ A，2009，503（1）：287－291.

［16］Defraigne P，Dehant V，Hinderer J.Stacking gravity tide measurements and nutation observations in order to determine the complex eigenfrequency of the nearly diurnal free wobble.J.Geophys.Res.，1994，99（B5）：9203－9213.

［17］孙和平，Ducarme B，许厚泽等.基于全球超导重力仪观测研究海潮和固体潮模型的适定性.中国科学（D辑），2005，35（7）：649－657.Sun H P，Ducarme B，Xu H Z，et al.Adaptability of the ocean and Earth tidal models based on global observations of the superconducting gravimeters.Science in China Series D：Earth Science，2005，48（11）：1859－1869.

［18］孙和平，徐建桥，Ducarme B.基于全球超导重力仪观测资料考虑液核近周日共振效应的固体潮实验模型.科学通报，2003，48（6）：610－614.Sun H P，Xu J Q，Ducarme B.Experimental earth tidal models in considering nearly diurnal free wobble of the Earth′s liquid core.Chinese Science Bulletin，2003，48（9）：935－940.