粒子群算法在极化SAR目标对比增强中的应用

张中山 ,余 洁, 孟云闪

（1.中国电子科技集团 第38研究所，安徽 合肥 230031；2.首都师范大学 资源环境与地理信息系统北京市重点实验室，北京 100048；3.中国科学院地理科学与资源研究所 资源环境信息系统国家重点实验室，北京 100101）

由于极化SAR成像过程的复杂性，在对其进行解译过程中常常会遇到2类目标的散射特性相近、影像差异不易区分的情况，使得解译过程变得尤为困难。极化SAR目标对比增强是指通过选取最优收发极化状态抑制杂波及干扰，突出感兴趣目标，其实质可抽象为带约束的最优化问题[1]。针对杂波环境中的目标极化增强，许多学者建立非线性规划模型、“三步法”等经典模型，并提出了目标增强问题的若干数值解法[2,3]，可分为2类：最优极化对比增强与极化两目标同零。最优极化对比增强的应用较广，其中的线性加权方法主要应用于分布目标，而SUMT数值求解方法既可以应用于分布目标，也可以应用于相干目标。但在该类方法的求解过程中，待求的参数个数较多，求解过程过于冗长、复杂。粒子群算法是一种基于群体智能方法的演化计算技术，具有很强的自组织性与适应性，概念简单、易于实现、具有全局搜索能力。针对极化SAR目标对比增强研究中存在的缺点，利用粒子群算法对极化目标对比增强问题进行解决将是一个有效的方法。

1 实验思路与流程

对于极化增强算法，极化SAR目标增强一般可抽象为带约束的最优化问题。在很多领域，智能优化算法已经替代了传统的数值计算方法，成为了求解寻优问题的最佳方案之一[4]。因此，本文采用粒子群算法解决极化SAR目标对比增强问题是可行的。

本文采用最为经典的三步法模型。该模型的思想在于以改变收发天线的极化状态来达到增强目的。雷达散射总功率P可以表示为：

式中，at为发送极化矢量；ar为接收矢量；S为Stokes矩阵。

根据矩阵论的知识，总功率P也可以改写为：

其中,

H为复数共轭转置。

总功率也可以转化为P=FH×CF的形式，其中，C为协方差矩阵。对于单基站来说，Shv=Svh，式(2)就简化成：

且协方差矩阵也变成了3×3的形式。

由文献[5]可知,

由式(3)可以得到：

A目标和B目标可以定义为：

一般来说，极化矢量可以转化为归一化的Stokes 矢量，且与椭圆角χ和方位角ψ有以下关系：

式中，m=t,r,（t为发送，r为接收）；δm=?v-?h是相位角差；极化状态可以写成如下形式：

文献[6]提供了一种通过中间变量将极化角、椭圆角和极化状态建立联系的方法：

式中，

图1 智能优化算法目标对比增强流程图

根据上面的推导可以得到逻辑框图，如图1所示。求解最优极化对比问题可以转化为求θm、dm的问题，同时，本文可以设定rab作为智能优化算法的适应度函数。

对于极化SAR目标对比增强问题，粒子群优化算法可以建立以下模型：

1）极化SAR目标增强中的函数可行解组合对应着粒子群优化算法中的粒子，即 1个（dt，θt；dr，θr）解对应着1个粒子。

2）同基于遗传算法的极化SAR目标增强算法类似，极化SAR目标增强中的最佳对比度对应着粒子群的适应度。

3）极化SAR目标增强中有带约束条件，在粒子群优化算法中采用约束性的粒子群优化算法（惩罚粒子群优化算法）改进。

4）极化SAR目标增强对比度的精度要求对应着粒子群优化算法的迭代终止阈值。

根据上述假设，基于粒子群优化算法的极化对比增强算法就可以使用以下步骤实现：

1）将统计得到的区域平均协方差矩阵作为粒子群优化算法的输入，随机初始化（dt，θt；dr，θr）粒子群。

2）通过计算am和F，计算出每个粒子的适应度值，更新粒子群的个体最优和全局最优值。

3）判断是否满足终止条件，即当达到最大循环次数或者连续迭代多次全局最优值不变时，退出迭代；否则，计算出方位角ψ和椭圆率角χ后，更新所有粒子的速度和位置，再循环至第2步。

2 实验结果与分析

2.1 实验数据

实验采用的数据是日本新泻地区(Niigata)的PiSAR数据(如图2所示)，已经过4视处理，空间分辨率是3m×3m，影像大小为1 200像素×1 200像素，该区域主要包括城区、河流、森林以及耕地。

图2 实验数据——Pauli基伪彩色合成图

2.2 实验方案

极化SAR目标增强实验算法采用C++编程，运行条件为P4 1.73 G CPU，1 G内存。

由于本文提出的智能优化算法的极化对比增强方法是针对协方差矩阵的，因此，采用线性加权的对比增强方法进行对比。另外，虽然有文献指线性加权的对比增强方法和SUMT解法的对比增强在本质上是一致的，但本文仍采用SUMT作为实验对象进行对比。在对比数据时，只给出对比度的数值。具体实验方案如下：

实验1：采用Niigata地区PiSAR数据，在图中选取2个区域，目标物为建筑物，抑制物为稻田。使用线性加权对比增强、SUMT、遗传算法和粒子群优化对这2个区域进行对比增强实验。此外，2种智能优化算法在种群个数和迭代效率上互相进行比较，以获得最佳算法。

实验2：仍然采用Niigata地区PiSAR数据，采用文献[7]选取的样本均值作为实验对象，进行线性加权增强、SUMT、和遗传算法、粒子群优化算法的对比。

2.3 实验结果对比

实验1：本实验采用日本Niigata地区影像进行目标增强，在图中选取A、B2个区域作对比实验（如图3所示），A区代表城市，B区代表农田，分别使用线性加权增强方法和智能优化算法增强方法进行对比。

图3 实验数据——SPAN影像

对A、B区域分别统计城市和农田的协方差矩阵如下：

再对A、B区影像进行4种方法的对比增强，如图4所示。从图4可发现，4种方法目视效果基本一致，都能把城市和农田区分开。可以明显地看出A、B区域均被增强了，即A区回波功率变大，而B区回波功率变弱。为了定量比较各种方法，进行对比度比较。需要说明的是，SUMT算法中采用的不是加权矢量。

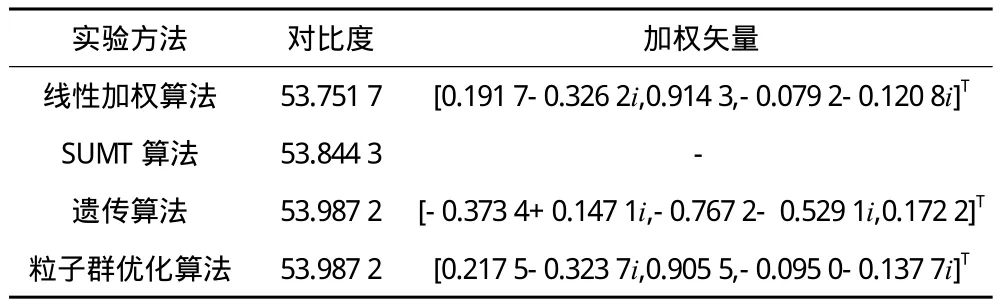
表1 实验1 目标对比增强结果统计表

通过实验可以发现，线性加权算法不管进行多少次实验，始终保持53.751 7 dB，这是因为线性加权方法使用的是拉格朗日算子，因此不会有任何改变。同时，无论是遗传算法还是粒子群优化算法，都能达到比线性加权算法更高的对比度。由表1可知，即使对比度相同，加权矢量还是截然不同的，这说明智能优化算法具有很强的多值搜索能力，搜索得到的结果也并不唯一。

为了对比2种智能优化算法的效率，本文主要采用群体个数（遗传算法为染色体个数、粒子群为粒子个数）和收敛次数来进行比较（如表2所示）。

图4 实验1：目标对比增强结果

表2 遗传算法和粒子群优化算法效率对比表

由表2可知，2种智能优化算法都在53.987 2 dB收敛，因此，可以认为此对比度是选取区域对比度影像的一个极值。当群体个数增大的时候，收敛次数明显降低。相对于遗传算法，粒子群优化算法只需少量的粒子、较少的迭代次数就能达到与遗传算法一样的对比度，因为粒子群优化算法在整个搜索过程中，粒子是跟随当前最优解的，从而能更快地收敛于最优解。

实验2：对于同一数据，本文采用文献[7]提供的样本数据，即选取城市和农田不同的区域进行对比增强：

采用线性对比增强算法、SUMT、遗传算法、粒子群优化算法分别进行比较，结果如表3所示。

表3 实验2:目标对比增强结果

从增强的对比度来看，可能由于文献样本数据精确到小数点后4位的问题，数值稍有差异，但是本文结论和文献的结论基本一致、从数据来看，粒子群优化算法在对比度上比线性加权要高。

上述实验可以证明，基于智能优化算法的极化对比增强能达到比传统的最优极化对比增强算法更好的对比度，而且实现较为简单。经2种智能优化算法对比可知，粒子群优化算法在增强效率上优于遗传算法。

3 结 语

本文主要针对极化SAR对比增强中存在的问题，提出了基于粒子群优化算法的最优极化对比增强方法。实验证明，粒子群优化算法具有强大的解决非线性约束问题的能力，在最优极化对比增强中，能达到比线性加权算法更高的对比度；粒子群算法具有很强的多值搜索能力，进行实验时，即使影像的对比度相同，使用的加权矢量仍然是不同的；并且粒子群优化算法在整个搜索过程中，粒子是跟随当前最优解的，可以更快地收敛于最优解。

[1]Swartz A A, Yueh H A, Kong J A.Optimal Polarizations for Achieving Maximum Contrast in Radar Images[J].Journal of Geophysical Research,1988,93:252-260

[2]Mott H, Boerner W M. Polarimetric Contrast Enhancement Coef-ficients for Perfecting High Resolution POL-SAR/SALK Image Featureextraction[J].SPIE, Wideband Interferometric Sensing and ImagingPolarimetry,1997,3120:106-117

[3]Loannidis G A,Hammers.D E Optimum Antenna Polarizations for Target Discrimination in Clutter[J]. IEEE Trans.on Antennas and Propagation,1979,27(3):357-362

[4]Su Ruelong. Optimal Polarization for Contrast Enhancement in Polarimetric Synthetic Aperture Radar Using Genetic Algorithms[D]. Taiwan: Sun Yat-sen University, 2003

[5]Cadzow A A, Yueh H A, Kong J A, et al. Optimal Polarizations for Achieving Maximum Contrast in Radar Images [J]. Journal of Geophysical Research-Atmospheres, 1988, 93 (B12): 15 252-15 260

[6]Sarabandi K,Li E S. Characterization of Optimum Polarization for Multiple Target Discrimination Using Genetic Algorithms. [J].IEEE Transaction on Antennas Propagate, 1999, 45 (12): 1 810-1 817

[7]汪洋. 极化合成孔径雷达图像处理及其应用研究 [D]. 合肥：安徽大学, 2007