库岸滑坡地质灾害三维演变动态显示方法

梁 欣，安 如，张发明，李 勇，蓝秋萍

（1.河海大学 地球科学与工程学院，江苏 南京 210098）

水库库岸滑坡是一种与水库安全运营密切相关的地质灾害。库岸滑坡分布于水库两侧，稳定性易变，一旦坍塌，破坏力巨大，可能造成河道堵塞及道路、桥梁损坏；其伴随产生的巨型涌浪，影响河道交通安全，甚至影响到对岸居民的生命安全。因此，水库库岸滑坡作为一项重大的地质工程及水电工程问题，一直是国内外学者广泛研究的焦点问题。

滑坡预测分析与建模模拟方面，Petley等对意大利一大型周期性活动滑坡的失稳模式进行了预测分析[1]；Lateltin等对瑞士国家滑坡进行了统一类别划分，并给出了相应的管理办法[2]；Xie等运用蒙特卡罗方法成功搜索最危险滑动面，建立了滑坡三维稳定性分析模型[3]；Tacher等探讨了在非均质地质条件下，渗透率与孔隙水压力对滑坡稳定性的影响[4]；Corominas在GIS技术支持下，从水位条件影响因子的角度对西班牙Vallcebre滑坡体稳定性进行了研究[5]；殷坤龙等运用非连续变形方法(DDA)对新滩滑坡的动态演变过程进行了模拟[6]。

滑坡涌浪数值计算及动画仿真方面，Geist等成功实现了滑坡灾害的三维演变过程模拟[7]；Marcello对滑坡涌浪的数值分析进行了三维研究[8]；潘家铮提出了滑坡入水初始涌浪的计算方法[9]。涌浪模拟几乎全部建立在理想化的数值计算基础上[7-13]，动画仿真多数建立在水波模拟的基础上。随着研究的深入，涌浪的动画模拟方法及模拟效果不断改善[13]。

在以往的滑坡三维演变过程动态模拟中，大多数采用VC结合OpenGL的方法实现，其基本思想是直接图形法，在数据操作中，往往以循环为基础展开，大大增加了数据操作的复杂性；在成图进行局部更新操作时，更体现出其可控制性不高的特点。祝文化等在IDL的支持下，以三峡库区榨坊坪滑坡体为例，详细阐述了滑坡体地面模型和滑动面三维模型的构建与可视化显示方法[14]，但尚缺少动态集成式的仿真模拟。本文采用IDL面向数组矩阵运算以及面向对象制图的基本思想，对三维场景中滑坡滑落、滑坡入水激起涌浪以及涌浪传播3个过程的动态集成显示进行了研究，简化了数据更新操作的难度，提高了对象的可控制性，各过程之间衔接平稳，整体稳定性高。

1 滑坡演变动态模拟机理

水库滑坡失稳运动过程是极其复杂的，因此，只能利用已知的数据结合理论对滑坡滑落全过程进行模拟，而难以做到完全仿真。

在本研究中，可以确定的滑坡要素主要有滑坡中心坐标、滑坡沿河长度、滑坡体主滑方向、滑坡体主滑方向长度、滑坡前缘高程、滑坡后缘高程、滑坡估算体积；水位要素主要有水库蓄水位高度以及滑坡在某蓄水位稳定性级别；涌浪要素主要有滑坡入水产生的涌浪高度。

本研究中，需要建立三维场景、滑坡和河道水面3个模型，并利用数组运算功能获取指定区域的数据，在面向对象制图思想的指导下，根据场景中的坐标等属性特点将3个模型依次添加进三维虚拟现实空间中。建立三维场景后，通过实时更新3个模型的属性来实现滑坡滑落、激起涌浪、涌浪传播等动态过程。滑坡三维演变过程的模拟设计思路如图1所示，从左侧启动（场景重置）开始。

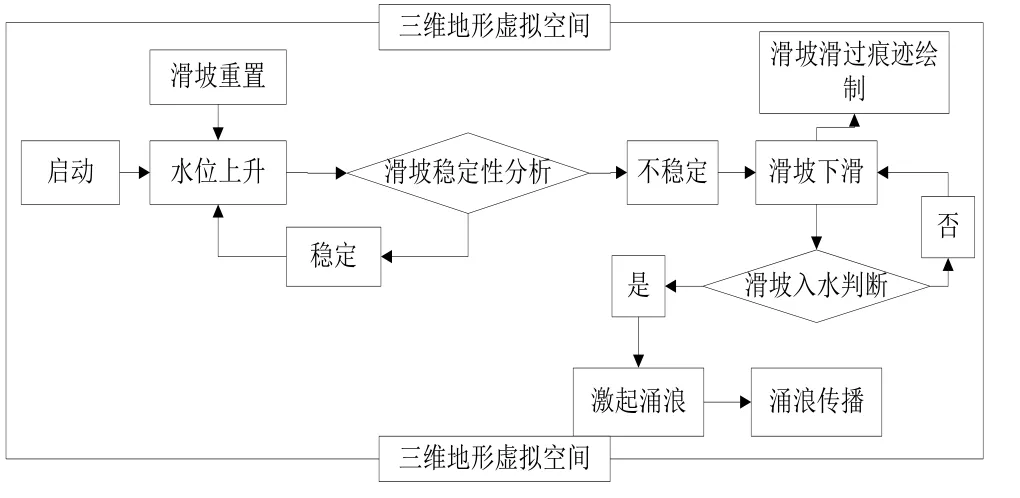
图1 水库滑坡滑落过程总体设计思路

2 滑坡演变动态过程场景的构建

IDL对象图形系统[15]是一个内建的对象类库，通过选择适当的内建对象、构造层次结构来创建图形场景。图形对象是功能性的封装，即每一个对象都包含自己独立的属性和方法，图形创建之后，数据及属性驻留内存之内，便于修改和反复使用。图2为本文对象层次结构,从下到上依次加入到上一级容器中。

图2 对象层次结构

2.1 三维地形对象的构建

地形数据的采集和输入是生成DEM模型的关键和基础。本文中地形数据的采集是根据地形等高线进行，通过二维等高线的矢量化，经过ArcGIS的处理获得 DEM数据。纹理映射是建立逼真三维地形场景的重要手段。地形纹理数据采用与DEM相同区域的高分辨率2.5 m SPOT5影像数据。

吕秋灵等采用层次细节方法和多分辨率模型方法，对三维地形的真实性研究做了阐述[16]。在实体建模中，IDL支持利用子块作为三维单元实体进行整个地形的三维显示，本文通过对DEM数据进行数据平滑计算后，运用GRID表面模型建模，建立三维地形。

2.2 河流水面与滑坡体对象的构建

河流水面层的绘制比较简单，只需要根据DEM数据和水位现状信息将等高面提取出来，然后再进行纹理映射即可。

滑坡体的绘制则要根据具体的滑坡中心点坐标、滑坡沿河长度、滑坡主滑方向长度、滑坡主滑方向4个要素来进行。由于滑坡实测数据的难得性，因此，在对滑坡4个地理要素（如图3所示）进行分析后，将滑坡形状在外部应用程序（如PhotoShop、Windows自带绘图工具等）中绘制出来（图3右下中间红色区域为滑坡部分，背景色设置为黑色），另存为图片，作为滑坡形状文件输入应用程序。在应用程序中，将滑坡中心点坐标、滑坡主滑方向、滑坡主滑方向长度、滑坡沿河长度等作为基本参数输入。在读取滑坡形状数据的同时，利用数组运算方法进行滑坡形状重构、滑坡在视图中的无损旋转等，再根据滑坡中心坐标，获取滑坡区域所对应的DEM数据。

图3 滑坡地理要素示意图

2.3 光照效果的添加

人类对光线强弱变化的反应，要比颜色变化灵敏度更高，添加光照在很大程度上增强了模型的立体感。因此，在三维场景绘制的最后添加光照。图4所示为三维场景构建结果。

图4 三维场景构建示意图

3 滑坡失稳运动过程数值计算

3.1 滑坡运动速度计算

国内外对于滑坡运动的研究有很多[17]，对滑坡运动速度的计算所采用的方法也很多，其中，应用最多的是把滑坡体作为斜面的运动质点，进而进行滑坡运动速度的计算。根据牛顿运动定律，滑坡运动方程为：

式中，为滑坡的质量；g为重力加速度；α为滑面倾角；f为动摩擦系数，f=tanφ；φ为动摩擦角；u为孔隙水压力；c为其他阻力，如粘聚力等。经推导：

式中，v为滑速；v0为初速；s为滑坡（质心）沿滑坡的滑距；H为滑坡（质心）的垂直降距；L为滑坡（质心）水平运动距离。

在实际运用中，H的数值近似采用滑坡中心的垂直降距，孔隙水压力和其他阻力等实测数据是很难得到的，在应用程序计算中，通常忽略u和c的影响，而改用f来综合反映，因此，提高了对f值的精确度要求。

3.2 滑坡入水激起涌浪高度的计算

潘家铮于1980年提出了初始浪高的计算方法[9]：当岸坡发生水平运动时，初始涌浪可表示为

当岸坡发生垂直运动时，初始涌浪可表示为

式中，ξ0为激起的涌浪初始高度（单位：m）；h为水库平均深度（单位：m）；v为岸坡水平运动速度（单位：m/s）；v″为岸坡垂直运动速度（单位：m/s）；g为重力加速度（单位：m/s2）。

f函数可表示如下：

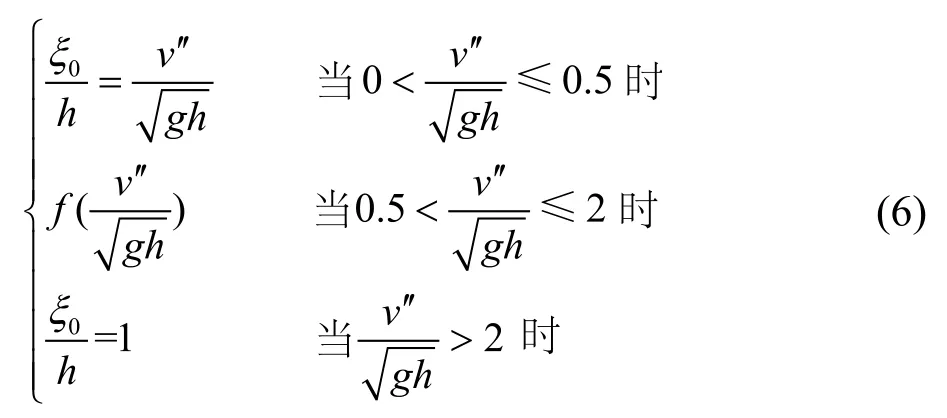
3.3 涌浪传播数值计算

贝塞尔方程是在圆柱坐标（球坐标）下使用分离变量法求解拉普拉斯方程和亥姆霍兹方程时得到的，因此贝塞尔方程在波动问题以及各种涉及有势场的问题中占有重要地位。本文涌浪传播过程中的数值计算采用第一类贝塞尔方程获得。第一类α阶贝塞尔方程Jα（x）是贝塞尔方程当α为整数或α非负时的解。

当α为整数时，贝塞尔的一种积分式为：

另一种积分表达式为：

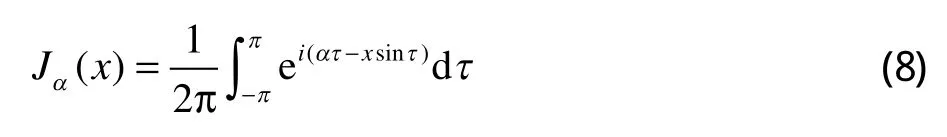
根据贝塞尔方程可以绘制出曲线、二维平面图以及涌浪传播的三维静态数值模拟图，如图5所示。

图5 贝塞尔方程曲线、二维贝塞尔数值平面、三维贝塞尔静态波动面（左图曲线100个点，中图512×512，右图为三维波动面数值静态图）

4 滑坡稳定性与模拟应用分析

4.1 滑坡稳定性分析

本文所选择模拟对象为澜沧江流域较大滑坡体，位于小黑江右岸，滑坡力学性质为牵引式，滑坡体物质组成以粘土和粉土夹碎块石为主，估算体积达到5 800 000 m3，滑坡深度约为20 m，滑坡沿河长度为640 m，主滑方向长度为320 m，属于古滑坡类型，河谷地貌类型属于U型谷。虽然天然状况下处于稳定状态，但在蓄水过后，大部分将被淹没，而且距离大坝较近，在蓄水位从812 m骤降到765 m时，滑坡极易发生，入水涌浪高度经估算达到40.35 m。滑坡一旦发生，到达大坝水位高度为1.28 m，涌浪冲击波将影响到大坝的安全运营。因此，在配合滑坡数值分析的情况下，本文利用已有数据对滑坡滑落过程进行三维可视化模拟，将二维数据直观表现出来，同时也可配合管理人员进行滑坡体的监测与管理。

水位骤降时，滑坡体内部孔隙水向坡体外渗流，导致土体强度参数降低，稳定系数降低。Fredlund[18]和张文杰[19]在对边坡稳定性影响的研究中，分别由饱和渗透系数、土-水特征曲线和极限平衡法得到了水位水文条件对边坡稳定性的影响规律。用摩根斯坦-普莱斯法计算该滑坡体稳定系数为0.93，毕肖普法计算稳定系数为0.91。由此可以得出，在水电站不断营运的过程中，在水位不断变化的情况下，滑坡极易失稳滑落。图6为水位由812 m骤降到765 m时的局部稳定性示意图，绿色区域为不稳定区域。

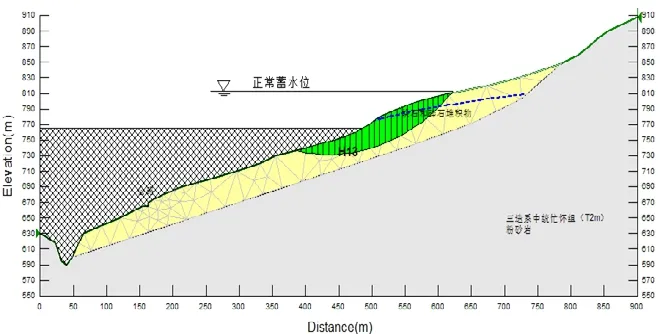
图6 水位由812 m骤降至765 m局部稳定性示意图

4.2 模拟应用

在实际滑坡入水过程中，滑坡入水产生连续不断的对水面的冲击力而激起涌浪，因此在考虑到运行效率以及真实性的前提下，本文采用将涌浪激发点设置在滑坡主滑方向线上，采用10次触发涌浪的方法制造连续涌浪，以此创造出涌浪不断被激起的起伏效果，提高模拟的真实性。图7为滑坡动态演变部分截图。

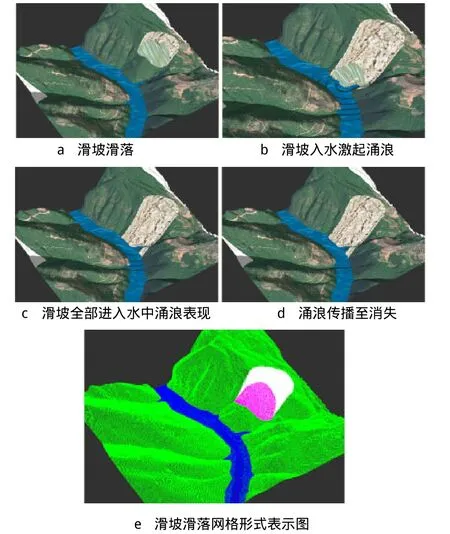
图7 滑坡三维演变动态局部截图

4.3 模拟分析

在滑坡数据量选择时，既要将滑坡整体区域全部截取出来，又要考虑到场景构建及滑坡数据运算的效率，因此本文选择的模拟数据量网格数量为1 024×1 024，实地距离范围为2 560 m×2 560 m。电脑硬件配置为Inter(R) Pentium(R) 2.00 GHz，内存为1.00 GB。滑坡过程发生时，每一次的滑坡绘制时间及水面绘制时间如图8（横轴为统计点个数Number，纵轴为时间Second）。

图8 滑坡绘制时间及水面绘制时间统计结果

通过图8可得到，滑坡体单次绘制平均时间为0.029 s，标准偏差为0.057，水面数据单次绘制平均时间为0.17 s，标准偏差为0.024 s。从整体的运行视觉效果观察（见图7），整个动态过程能够平稳衔接起来，并且在有一定的时间间隔的情况下，滑坡滑落及涌浪的传播2个连续不断的过程能够更真实地表现出来。在将整个对象按照图2规则划分为多个模型的基础上,使用数组矩阵运算，简化了模型数据更新的难度，数组元素的调用更直观、灵活[15]。图7的模拟结果显示，整个模拟过程运行稳定性高；图8的时间统计结果说明了各子过程之间能够平稳过渡。结果表明，整个滑坡动态演变过程之间衔接平稳，各对象数据操作简便，对象的可控制性高，整体稳定性好。

5 结 语

本文以澜沧江糯扎渡水电站某大型滑坡为例，通过数值分析及现实计算，成功实现了滑坡失稳滑落、滑坡入水激起涌浪、涌浪在河道传播三者的无缝结合，较好地完成了滑坡滑落全过程的动态模拟。此次研究为后期运用DDA方法进行滑坡三维演变的动态显示提供了有力的支持。面相对象制图思想的成功应用，满足了“应对变化，提高复用”的要求，降低了数据处理与制图具体算法之间的耦合度，不仅使程序本身具有更高层次的抽象度，而且具有高度的易扩充性和安全性。本文研究表明，程序文本层次结构简单分明，理论与实际操作耦合度高，方法应用灵活性高。

[1]Petley D N, Mantovani F, Bulmer M H, et al. The Use of Surface Monitoring Data for the Interpretation of Landslide Movement Patterns[J]. Geomorphology, 2005，66(1): 133-147

[2]Lateltin O, Haemmig C, Raetzo H, et al. Landslide Risk Management in Switzerland[J]. Landslides, 2005，2(4): 313-320

[3]Xie M, Esaki T, Zhou G Y. Geographic Informationsystemsbased Three-dimensional Critical Slope Stability Analysis and Landslide Hazard Assessment[J].Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(12): 110-118

[4]Tacher L, Bonnard C, Laloui L, et al. Modelling the Behaviour of a Large Landslide with Respect to Hydrogeological and Geomechanical Parameter Heterogeneity[J]. Landslides, 2005，2(1): 3-14

[5]Corominas J,Santacana N. Stability Analysis of the Vallcebre Translational Slide, Eastern Pyrenees (Spain) by Means of a GIS[J].Natural Hazards,2003，30(3): 473-485

[6]殷坤龙, 姜清辉, 汪洋.新滩滑坡运动全过程的非连续变形分析与仿真模拟[J].岩石力学与工程学报,2002，21(7): 959-962

[7]Geist E L, Jakob M, Wieczorek G F,et al. Preliminary Assessment of Landslide-induced Wave Hazards, Tidal Inlet, Glacier Bay National Park, Alaska[R].Department of the Interior and US Geological Survey,2003

[8]Risio M, Girolamo P, Bellotti G, et al. Three-dimensionalExperiments on Landslide Generated Waves at a Sloping Coast[J].Coastal Engineering, 2009，56(5):659-671

[9]潘家铮.建筑物的抗滑稳定和滑坡分析[M].北京:水利出版社,1980

[10]Fritz H M, Hager W H, Minor H E. Landslide Generated Impulse Waves 2: Hydrodynamic Impact Craters[J]. Experiments in Fluids, 2003，35(6):520-532

[11]周剑华.水库滑坡涌浪灾害的数值研究[J].长江科学院院报,2003，20(2):7-9

[12]李未,王如云,张长宽.滑坡涌浪的产生与传播波形分析与计算[J].水科学进展, 2004， 15(1): 45-49

[13]宁德志.快速多极子边界元方法在完全非线性水波问题中的应用[D].大连:大连理工大学,2005

[14]祝文化, 田金华, 池秀文，等.IDL支持下的滑坡可视化方法研究[J].武汉理工大学学报,2004，26(8): 55-56

[15]韩培友.IDL可视化分析与应用[M].西安:西北工业大学出版社,2006

[16]吕秋灵, 张俊霞. 三维地形可视化及其实时显示方法[J]. 河海大学学报: 自然科学版, 2002，30(4): 85-87

[17]汪洋, 殷坤龙.水库库岸滑坡速度及其涌浪灾害研究[D].武汉:中国地质大学, 2005

[18]Fredlund D G, Xing A, Fredlund M D, et al. The Relationship of the Unsaturated Soil Shear Strength Function to the Soil Water Characteristic Curve[J]. Canadian Geotechnical Journal,1995，32:440- 448

[19]张文杰,詹良通,凌道盛,等,水位升降对库区非饱和土质岸坡稳定性的影响[J].浙江大学学报:工学版, 2006，40(8):1 365-1 370