基于MATLAB的摄像机标定研究与实现
2013-06-25华舒悦杨龙
华舒悦 杨龙
(1. 华南理工大学 软件学院,广州 510006;2. 华南理工大学 计算机科学与工程学院,广州 510006)
立体视觉是机器人技术研究中最为活跃的一个分支,也是机器人智能化的重要标志。双目立体视觉的基本原理是模仿人类的立体视觉,从两个视点观察同一景物,获取不同视角下的感知图像,从而得到像素间的位置偏差图像即视差图,再结合三角测量原理即可得到景物的三维信息[1]。为获得景物的三维信息,首先需要对两个摄像机进行立体标定得到两个摄像机的内外参数和畸变参数。得到此参数后即可对图像进行立体校正(stereo rectify),经过立体校正的图像在像素层面上是行对齐的,这样处理可以为后面的立体匹配大大减少计算量,从二维的搜索缩小到一维的搜索[2]。立体匹配过后即可得到视差图而得到三维信息。可见摄像机标定是整个双目立体视觉的基础。
1 摄像机模型和畸变
摄像机的模型是经典的针孔模型[3]。在此模型中,想象着光线是从场景或很远的物体发射过来的,但仅仅只是一条光线。如图1 所示,f 是摄像机焦距,Z 是摄像机到物体的距离,X 是物体的长度,x 是图像平面上物体图像。光轴与图像平面的交点被称为主点。其数值可以通过相似三角形-x/f =X/Z 得到,或

通过数学抽象将针孔摄像机模型整理为一种等价形式,使其形式更为简单。在图2 中,交换针孔和图像平面,这样就形成了更加容易理解的三角形相似关系x/f=X/Z。负号去掉了,因为物体不再是倒立的。
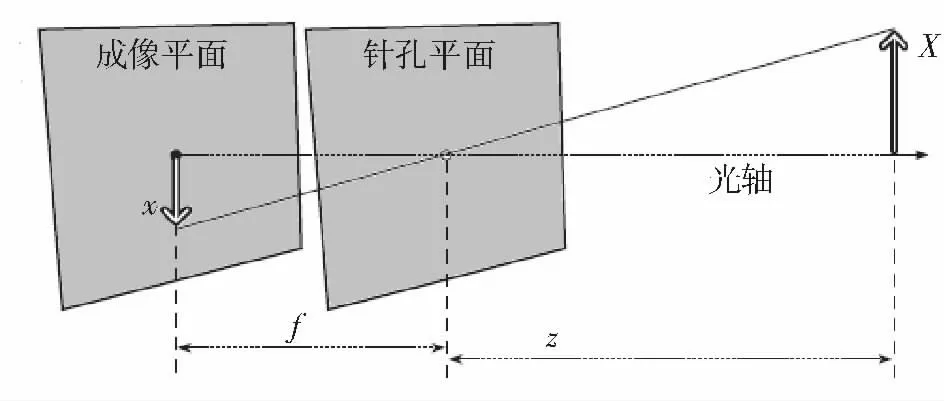
图1 针孔模型

图2 针孔模型的数学等价形式
实际中主点和成像仪并不重合,为此我们引入两个心的参数cx和cy。对可能的偏移建模。这样,物理世界中的点Q(X,Y,Z)以某些偏移方式投影到成像仪平面上点(xscreen,yscreen),如下所示:

在此引入了两个焦距,主要是由于单个像素点在成像仪上是矩形而不是正方形。
那么将物理世界中的点投影到摄像机上,可以用下式表示:

上面的M 矩阵即为摄像机的内参数矩阵。
采用理想的针孔,有了一个最原始的视觉模型。但是,由于只有少量的光线通过针孔,这导致因曝光不足使得图像生成很慢。对于实际的摄像机而已,必须利用大面积且弯曲的透镜,让足够多的光线能够收敛聚焦在投影平面上。透镜的引入使得我们可以很快的曝光并得到图像,但是由于实际制作工艺透镜都会有畸变。
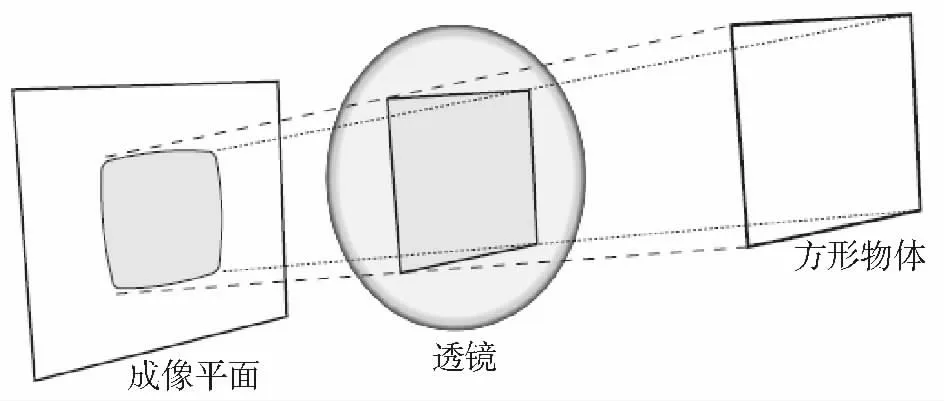
图3 径向畸变

图4 切向畸变
透镜的畸变主要有径向畸变和切向畸变。分别如图3 和图4 所示。径向畸变在成像仪的中心的畸变为0,随着向边缘移动,畸变变得越来越大,这可以用r=0 位置周围的泰勒级数展开的前几项来定量描述。对于成像仪上的畸变点(x,y),可以将其校正为(xcorrect,ycorrect),其中:

对于径向畸变可以用额外的两个参数p1和p2来描述,如下:

从上面可以看出,对于一个摄像机有4 个内参数和5 个畸变参数,对摄像机标定就是求解这9 个参数,以此来建立零失真和零畸变摄像机模型。

图5 立体视觉模型
2 立体视觉模型
假设有一套无畸变、对准、已测量好的完美标准试验台,如图5 所示,两台摄像机的像平面精确位于同一平面上,光轴严格平行(光轴是从投影中心O 朝像主点c 方向引出的一条射线,也称为主光线),距离一定,焦距相同fl=fr。物理世界中的点P 在左右图像上的成像点为pl和pr,相应的横坐标分别为xl和xr。视差即定义为d=xl-xr。利用相似三角形可以很容易的推导出Z。

在上式里,T 为左右摄像机的成像仪中心的距离,叫做基线长。分母为视差。可以看出深度Z 和视差d是成反比。图6 是立体视觉在OpenCV 中使用到的二维和三维坐标系统。左右成像仪的像素原点都在图像的左上角,像素坐标分别记为(xl,yl)和(xr,yr)。投影中心为Ol和Or,主光线与图像平面相交于(cx,cy)。经过数学校正,摄像机就是行对准(也即像素层面的对准),且相距T,相同的焦距为f[4]。
通过上面对摄像机模型和立体视觉模型的讨论,可以得出如下公式:
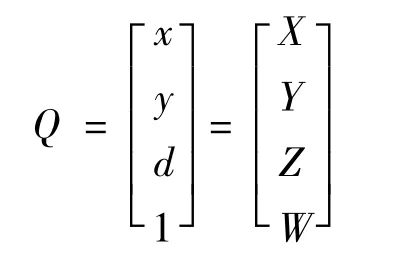
其中Q 为重投影矩阵,其定义如下:

Q 中的参数,通过对摄像头进行单个标定和立体标定就能得到。因此,给定一个二维齐次点和其关联的视差d,可以将此点投影到三维中:

三维坐标就是(X/W,Y/W,Z/W)。
3 实验
摄像机标定分为单个摄像机标定和双目立体标定,单个摄像机标定就是为了求解第1 节末尾提到的9 个参数。而立体标定是建立场景中某点的三维几何位置与其在摄像机图像中对应像素点位置之间的关系,包括右摄像头相对于坐摄像头的坐标和旋转矩阵[5]。其途径是依据摄像机的几何模型,由已知特征点的世界坐标和图像坐标来计算摄像机的模型参数。标定板和摄像机分别如图6 和图7 所示。

图6 标定板

图7 双目摄像机
本文中摄像机标定采用的是MATLAB 的标定工具箱,这个工具箱界面友好,最重要的是它的标定结果比OpenCV 稳定和精准。在标定的过程中,对两个摄像机采集的每一幅标定板图像手动采集4 个最边上的角点。MATLAB 会找出整幅图像中的所有角点,并用红色的十字形标出来[6]。
对两个摄像机分别标定完毕后,会生成一个Calib_ results. mat 的矩阵,将其改名后保存着两个矩阵在同一个目录下面,并运行立体标定,即可完成所有的标定过程。最终的标定结果如图所示。

图8 所有标定图片

图9 提取角点

图10 标定结果
从上图的标定结果中,其实就已经求出了左右摄像机的内参数矩阵,已经立体标定生成的旋转矩阵和平移矩阵,分别如下所示。
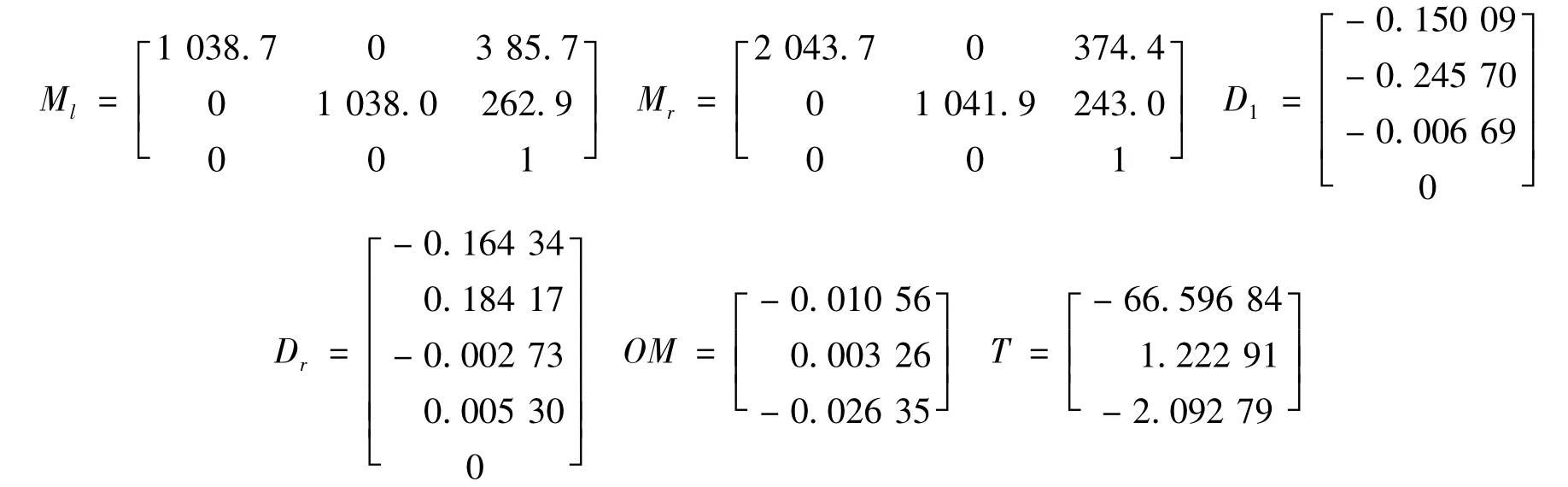
在上面,M1和Mr分别为左右摄像机的内参数矩阵,D1和D2分别为左右摄像机的畸变参数,OM为旋转矩阵,经过Rodrigues 变换后可以变成3 ×3 的旋转矩阵,T 为平移矩阵。至此,摄像机的各种参数已经获得。它们是后续的三维重建等高层应用必不可少的参数。
4 结语
分析了摄像机的模型和立体视觉模型,得出要实现三维重建必须知道摄像机的各种参数的结论。在MATLAB 工具箱基础上对双摄像机进行标定,得出了各种摄像机参数。实验结果表明此方法可靠,有效。
[1]Gary Bradski.学习OpenCV[M].于仕琪,译.北京:清华大学出版社,2009.
[2]冈萨雷斯.数字图像处理[M]. MATLAB 版.阮秋琦,译.北京:电子工业出版社,2005.
[3]张广军.机器视觉[M].北京:科学出版社,2005.
[4]黄侃.计算机立体视觉中的摄像机标定算法的研究与应用[D].沈阳:沈阳工业大学,2007
[5]康晶.基于立体视觉摄像机标定方法的三维重建技术研究[D].长沙:湖南大学,21-39.
[6]尹力.基于OpenCV 的计算机视觉三维重建方法研究[D].合肥:安徽大学,19-32.
