用虚时间传输计算偶极孤子

陈桂华 罗志环

(1. 东莞理工学院 电子工程学院，广东东莞 523808;2. 华南农业大学 应用物理系，广州 510642)

孤粒子波，简称孤子，是一种在非线性作用下形成的自局域态。孤子在运动过程中可以长时间地保持形状而不坍塌，因而在许多学科中都有重要的应用。目前，具有孤子解的方程主要有KdV 方程，Sine－Gorden 方程以及非线性薛定谔方程，而非线性薛定谔方程由于可以同时解释光场的非线性传输以及冷原子在波色－爱因斯坦凝聚下的行为在近20年受到人们极大的关注，其中研究非线性薛定谔方程在各种情形下的孤子解是人们重点关注的一个方向。在数值计算方面，人们发展了许多算法来研究这一问题，其中比较著名的算法有打靶法、牛顿法、松弛法和虚时间传播方法等。打靶法和牛顿法主要适用于一维问题，松弛法虽然也适用于一维问题，但较前两种方法复杂，因此更多地应用于二维问题。而虚时间传播方法由于比较简洁明了且可以方便地与各种算法相结合(比如，与Crank-Nicolson 算法或者分布傅立叶算法结合)，适用于一维和二维问题，因而备受大家欢迎。

近年来，许多的研究成果都是基于虚时间传输方法［1－2］，如何改进或者提高虚时间方法的收敛性，是人们一直关注的问题［3］。虚时间传输方法的本质是利用迭代寻求最低能量状态，最低能量状态就是基态，因此它一般只能处理基态解的问题，而对于激发态则无能为力。激发态孤子，特别是第一激发态的孤子(即偶极孤子)，也是人们所关注一类孤子问题，如如何使得虚时间方法可以适用于研究偶极孤子问题，成为推广虚时间方法应用的一个重要方面。本文通过引入宇称条件，对虚时间方法进行改进，使得用虚时间方法进行迭代的时候有机会捕捉到第一激发态，从而让虚时间方法也可以处理偶极孤子。本文以反相非线性光子晶体中的偶极孤子为例，对改进的虚时间方法进行模拟检验。结果表明，该方法可以用来寻找偶极孤子。

本论文结构上主要分为四部分。第一部分为引言。第二部分将对虚时间方法进行简单介绍，并在算法中引入宇称条件，使得虚时间方法可以捕捉到偶极孤子解。在第三部分中，我们以反相光子晶格中的偶极孤子为例，验证方法的有效性。在最后部分，我们将对全文做一个总结。

1 虚时间传播方法

给定初态，原则上可以根据上述表达式，得到今后任意时刻态的表达式。假设τ =－it，其中τ 称为虚时间，同时只针对一维情况考虑，则方程(1)变成:

我们用系统的本征函数系{uj}(我们假设系统的本征函数是正交完备的)对初态ψ(x，0)进行展开:ψ(x，0)=cjuj，其中cj为展开系数。假如{uj}为已知，原则上cj可以由内积(uj，ψ(x，0))求得。然而，在我们的问题里面{uj}本身是一个待求的未知函数系，因此cj也是一个未知量。把波函数展开式代入方程(2)可得:

从上式我们可以看到，由于e－Ejτ是一个指数衰减函数，因此随着虚时间τ 的增加，Ej值越大的态将会衰减得越快。在τ 的增加的过程中，基态的存活时间是最长的，方程(3)存在如下结果:

也就是说，随着虚时间τ 的增加，ψ(x，0)将会演化出系统的基态波函数，因此，该方法称之为虚时间传播(Imaginary Time Propagation 简称ITP)，然而该方法的一般只能用于求基态问题，对于激发态的求解，则需要作特殊的处理。

本文通过引入一个宇称条件，使得ITP 方法也可以处理第一激发态。量子力学指出，体系的第一激发态具有奇宇称，简单地说，在一维问题中，是一个奇函数。用数学表达式可以表述为

我们可以把这个宇称条件，强制设置到虚时间传播方法中，让波函数在迭代的过程中强行保持这一关系，从而使得波函数收敛于第一激发态。下面我们将以反向非线性晶格孤子为研究对象，以验证上述方法的有效性。

2 虚时间求解反相光子晶格中的偶极孤子

对于一般的光学材料而言，光疏媒质对应低非线性折射率，光密媒质对应高非线性折射率。然而，对于某些可以和光场发生共振相互作用的物质，通过调节进入阵列的探测光场与能级之间的失谐量，可以实现光疏媒质具有高非线性折射率而光密媒质具有低非线性折射率。这些物质周期性地排列起来，就组合成反相非线性晶格阵列波导。制作反相光子晶体有多种方案，比如把高强度激光作用在硅上，通过光刻，可以形成上述关系的晶格［4－5］。又或者把三价鐠离子(Pr3+)周期地参杂到YSO 晶体中，利用电磁感应透明，也可以形成上述关系的晶体［6－7］。最近发现，把燃料诺丹明B 周期参入光刻胶SU8 中，可以形成具有饱和非线性的反相光子晶体［8－10］。反相非线性晶格阵列波导有很多特性。由于晶格势阱区域与非线性区域互为反相，导致了晶格的线性效应与非线性效应互相竞争，使得光场产生很多奇异的非线性效应，因此在光传输器件中，有重要的潜在应用价值。目前，在反相光子晶格中，基态孤子解的性质已经研究得比较多，而对其第一激发态的孤子解，也就是偶极孤子(dipole soliton)，目前的研究还是鲜有报道。

光场在具有克尔非线性的一维反相非线性光子晶体(如图1 所示)中的传输可以由以下一维无量纲的非线性薛定谔方程来描述［5］:

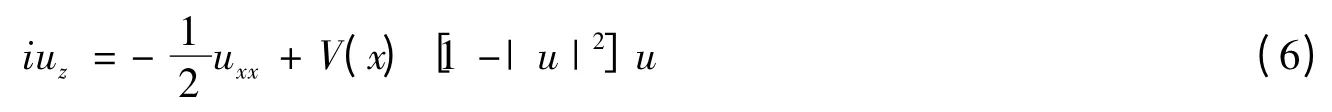
在方程中V(x)=V0R(x)，其中R(x)是高度为1 的周期方势阱(如图1 所示，也就是固体物理中的克莱恩－戈登势)，势阱和势垒的宽度分别为d1和d2，V0为势阱的调制深度。光场的功率定义为

我们采用虚时间方法对以上模型进行模拟，求解其偶极孤子，即第一激发态孤子。具体的程序可以归纳成以下6 个基本步骤:

图1 反相非线性晶格阵列波导

1)选择一个初始猜测解ψ(x，0)。对于激发态来说，此解一般是一个具有奇宇称的试探波函数，对于该一维问题来说，就是一个奇函数;

2)利用差分或者分步傅立叶对非线性薛定谔方程做虚时间演化;

3)演化后强制执行宇称条件，即方程(5);

4)对奇宇称处理后的波函数进行归一化，让其功率等于初始功率，以下为归一化公式:

5)设置一个误差函数，为前后两次演化所得波函数的形状差

6)设置一个收敛的阈值EPS，如果Errn＞EPS，则重复(2)－(5);如果Errn＜EPS，则终止循环，所得的最终波函数即为我们需要求的波函数。

图2 方程(7)的基态孤子解，其中P=10，V0 =0.02，d1 =d2 =10

在上述步骤中，假如我们不执行步骤3，我们将会得到如图2 所示的基态孤子解，但是在添加了步骤3 之后，我们就可以得到偶极孤子解，图3 给出了偶极孤子的一个数值例子。

从图3 可以看出，引入宇称条件后，我们可以在反相非线性光子晶体中寻找到稳定的偶极孤子解。

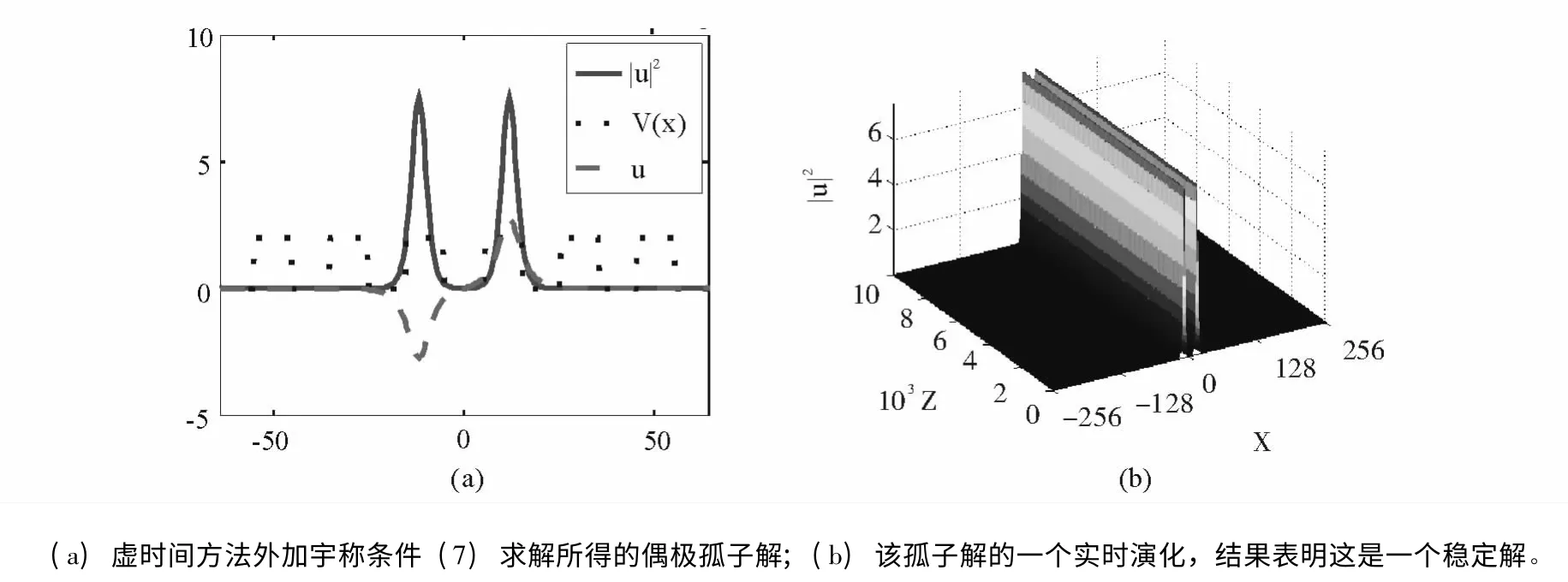
图3 方程(7)的基态孤子解，其中P=78，V0 =0.02，d1 =d2 =10

3 结语

虚时间传播方法是研究非线性薛定谔方程基态解的重要方法，它无论在非线性光学或者在玻色爱因斯坦凝聚中都有重要的应用价值。传统的虚时间方法，一般只适用于求解基态解，对于激发态的解则往往无能为力。在本文中，我们通过引入宇称条件，使得虚时间传播方法可以处理第一激发态解的情况。此方法对研究各类用非线性薛定谔方程描述的非线性系统有重要的应用价值。我们把该方法运用到处理反相光子晶格中的孤子问题，并寻找到偶极孤子的存在。

［1］Chiofalo ML，Succi S，Tosi MP. Ground state of trapped interacting Bose-Einstein condensates by an explicit imaginary-time algorithm［J］.Physical Review E，2000，62:7438.

［2］Li Y，Pang W，Chen Y，et al. Defect-mediated discrete solitons in optically induced photorefractive lattices［J］. Physical Review A，2009，80:043824.

［3］Yang J，Lakoba TI. Universally-Convergent Squared-Operator Iteration Methods for Solitary Waves in General Nonlinear Wave Equations［J］.Studies in Applied Mathematics，2007，118:153.

［4］Kartashov YV，Vysloukh VA，Torner L. Soliton modes，stability，and drift in optical lattices with spatially modulated nonlinearity［J］. Optics Letters，2008，33(15):1747.

［5］Kartashov YV，Vysloukh VA，Torner L. Power-dependent shaping of vortex solitons in optical lattices with spatially modulated nonlinear refractive index［J］. Optics Letters，2008，33(19):2173.

［6］Li Y，Malomed BA，Feng M，et al. Arrayed and checkerboard optical waveguides controlled by the electromagnetically induced transparency［J］. Physical Review A，2010，82:063813.

［7］Li Y，Malomed BA，Feng M，et al. Double symmetry breaking of solitons in one-dimensional virtual photonic crystals［J］. Physical Review A，2011，83:053832.

［8］Feng M，Liu Y，Li Y，et al. Light propagation in a resonantly absorbing waveguide array［J］. Optics Express，2011，19:7222.

［9］Li J，Liang B，Liu Y，et al. Photonic crystal formed by the imaginary part of the refractive index［J］. Advanced Materials，2010，22(24):2676.

［10］Li Y，Malomed BA，Wu J，et al. Quasicompactons in inverted nonlinear photonic crystals［J］. Physical Review A，2011，84:043839.