分数阶PID控制运用于励磁控制系统
2013-06-23于莲芝成羚羚
于莲芝, 成羚羚
(上海理工大学光电信息技术与计算机工程学院,上海 200093)
分数阶PID控制运用于励磁控制系统
于莲芝, 成羚羚
(上海理工大学光电信息技术与计算机工程学院,上海 200093)
针对传统的PID(proportion integration differentiation)控制器已难以满足励磁控制系统动态、静态性能以及遏制干扰能力的要求,采用比传统的PID控制器多了两个参数的分数阶PID(FOPID)控制器.该控制器调节的范围更加广泛,能够很好的适应当前励磁控制系统的需要.对其控制器与PID控制器做了对比仿真,结果表明:分数阶PID控制器具有优于传统PID控制器的性能.
励磁系统;PID控制;分数阶PID控制
随着我国大容量发电机组的投入运行以及超高压远距离和直流输电的混合电网建设,全国性的电力系统逐渐形成,全国电网将发生巨大变化.电力系统的不断扩大,使电力系统的结构和运行方式变得越来越复杂多变,对电力系统的综合科学技术水平的要求也越来越高,使得电力系统的技术更新速度大大加快,不同技术之间互相渗透,相互融合也越来越普遍.
同步发电机励磁控制系统在保证电能质量、无功功率合理分配和提高电力系统稳定性等方面都起着十分重要的作用.同步发电机是将旋转形式的机械功率转换成三相交流电功率的设备,为了完成这一转换并满足运行的要求,除了需要原动机——汽轮机或水轮机供给动能外,同步发电机本身还需要有可调节的直流磁场作为机电能量转换的媒介,借以调节同步发电机运行工况以适应电力系统运行要求.为同步发电机提供可调励磁电流的设备总体,称为同步发电机的励磁系统[1].
分数阶PID控制器由Podlubny[2]提出,其一般格式简记为PIλDμ.实际系统中有许多是分数阶的而不是整数阶的,之所以将它们作为整数阶系统来考虑是由于其复杂性.由于分数阶控制器的阶次为任意实数,因此分数阶控制器与整数阶控制器有所不同,整数阶PID控制器只是分数阶PID控制器的特例.随着电力系统的发展,对系统运行的可靠性和动态品质要求越来越高,传统的PID励磁控制器已经不能满足这一要求,采用分数阶PID控制策略在同步发电机中的应用以期取得良好的控制效果.
1 分数阶PID控制器
1.1 分数阶微积分[3]简介
分数阶微积分的基本操作算子定义为


式中,h为计算步长;Γ()为欧拉Gamma函数;[]取整函数.实际应用中,式(2)和式(3)定义等价,但RL定义常用于公式运算,而GL定义则用于数值求解.
当n-1<p<n时,对RL定义求拉普拉斯变换,有

1.2 分数阶微积分的滤波算法
在实际运用中,这两种分数阶微分运算方法运算的前提是f(t)为已知函数,但在实际运用该函数有可能未知,所以需要用其它方法来求取分数阶微分,例如通过构造滤波器的方式对信号进行数值微分处理.
信号的滤波可以有连续和离散两种形式,分别用来拟合Laplace变换算子Sλ和Fourier变换算子(jω)γ.从效果上看,函数的分数阶数值相当于原来信号需要通过这样的滤波器得出输出信号.
文献[4]介绍了Oustaloup算法.假设选定的拟合频率段为(ωb,ωh),则可以构造出的连续滤波器的传递函数模型为

式中,U(s)为输出;E(s)为偏差;Kp为比例系数;Ti为积分时间;Td为微分时间.
1.3 分数阶PID控制器
与整数阶PID控制器相似,分数阶PID控制器的微分方程为

由于λ和μ为任意实数,所以常规PID控制为分数阶PID控制的特例.根据被控对象的阶次不同,可以选择不同的λ和μ值,以得到最佳控制效果.由于λ和μ可以连续的变化,因此,分数阶PID控制器较整数阶PID控制器更具有灵活性.如图1所示,整数阶PID控制只能在OABC 4个点之间PPI-PD-PID,而分数阶PID可以取平面上的任何点.设0<λ≤1,以0<μ≤1,则控制器的阶次λ和μ可以在图1中的阴影区域内任意取值.这就使得分数阶PID控制器的结构更加灵活、更适合于分数阶系统的动态特性[5].
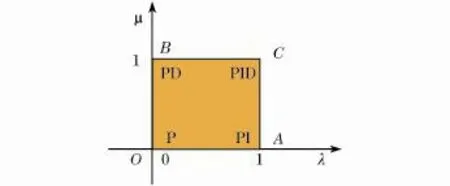
图1 PIλDμ控制器示意图Fig.1 PIλDμcontroller diagram
2 分数阶PID控制与PID控制励磁仿真研究
在MATLAB的Simulink下构建分数阶PID控制与PID控制励磁的模型,得到其对比图,这里用滤波法实现分数阶PID.
图2为简单励磁系统下的分数阶PID与PID控制模型.在这个简化的系统里,输出为电机输出的电压,示波器显示的是测量的标幺值电压.在这个系统里加入了干扰环节Interference,将用于比较PID与分数阶PID在遏制干扰时的效果.在本文中使用的干扰为短路干扰,持续0.1 s.

图2 简单励磁系统仿真图Fig.2 Simulation diagram of simple excitation system
图3为PID控制器和分数阶PID控制器的内部结构.图4为分数阶微积分的封装模块和干扰模块.仿真中,PID控制器的参数为Kp=85,Ki= 0.25,Kd=4.5;分数阶PID控制器参数为Kp= 85,Ki=0.25,Kd=4.5,λ=1.1,μ=1.6.
图5为同步电机在PID控制器和分数阶PID控制器控制下的启动对比图.从图中可以明显看出分数阶PID控制器的控制动态性能要好于PID控制器,虽然分数阶PID控制器调节时间稍长于PID控制器,但超调量等其它动态性能分数阶PID控制器都有优势.
图6为在短路和断路小干扰下PID控制器与分数阶PID控制器的比对.可以明显看出分数阶PID控制器的动态性能要优于PID控制器.

图3 PID控制器与分数阶PID控制器Fig.3 PID controller and fractional PID controller

图4 分数阶微积分和干扰模块Fig.4 Fractional order calculus and the interfere module
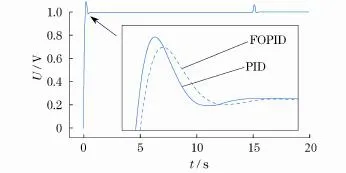
图5 同步电机启动Fig.5 Synchronous motor starting
3 基于PSB(电力系统模块)的新型控制器控制效果
研究分数阶PID、PID建立的单机无穷大系统中的控制效果,主要以电机的机端电压为研究对象,因为在电厂中,往往要求电机在恒压下工作,所以主要分析机端电压,给出了同步发电机母线端口相电压的仿真分析.
实验主要有三相断线、三相短路和原动机干扰实验.所有的实验的仿真时间均为30 s,且故障时间为15~15.1 s.在下文的仿真图中,默认实线为分数阶PID控制器,点划线为PID控制器.
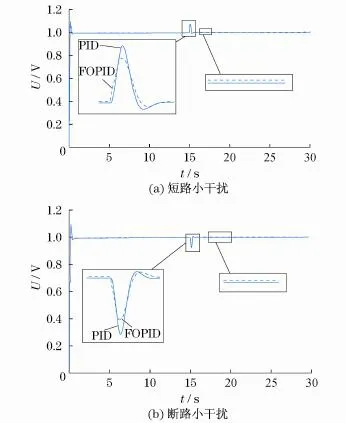
图6 短路小干扰与断路小干扰对系统的影响Fig.6 Small short circuit interference and circuit interference effect on the system
同步电机的参数分别为额定容量200 MVA、定子额定电压13.8 kV、定子额定频率50 Hz、直轴同步电抗1.305Ω、暂态直轴同步电抗0.296Ω、次暂态直轴同步电抗2.525Ω、纵轴同步电抗0.474Ω、次暂态纵轴同步电抗0.243Ω、漏抗0.18Ω、直轴开路时间常数1.01、暂态直轴短路时间常数0.053、暂态交轴短路时间常数0.1.
分数阶PID的参数为

4 启动、短路、断路实验结果
在8~8.1 s时加上一个断路小干扰;在12~12. 1 s时加上一个短路小干扰.实验结果如图7所示.

图7 启动、短路、断路机端电压Fig.7 Start,short,circuit and open circuit voltage of the machine
从启动、短路、断路机端电压可以看出,分数阶PID超调量小于PID,调节时间都比较好,所以在不影响速度的情况下,分数阶PID控制是优于PID控制的.
5 小 结
现代工业的发展和人们生活水平的日益提高,对电力系统稳定性的要求越来越高.从上世纪60年代以来,励磁控制对提高电力系统的稳定性起了很重要的作用,目前励磁控制在电力系统中的作用越来越大.而在目前,大多数的励磁控制器还是传统的PID,但其对于日益要求严格的电网来说,显然已经很难达到人们的要求.所以研究了一种新型励磁控制器.
研究均表明分数阶PID控制器能取得比传统PID更好的效果.但同时,在研究的过程中发现,分数阶PID与PID控制器都存在一些缺点.在分数阶PID中,由于其控制量与过去的每一个控制量都有关,所以其消耗大量的内存和计算机时间,这在实际控制中显然是不可行的.但同时也发现其控制量与靠近它的过去时刻关系最大,如果能找出这个范围,那么其在实际中会取得良好的效果.
本文仅仅对分数阶PID与PID控制器进行了部分的研究,对于其进一步的改进将在以后的工作中进一步的研究.
[1] 杨德先,陆继明.电力系统综合实验原理与指导[M].北京:机械工业出版社,2004.
[2] Podlubny I.Fractional-order systems and PI,D1-controllers[J].IEEE Trans on Automatic Control,1999,44(1):208-214.
[3] 秦君琴.分数阶微积分的性质[J].江苏师范大学学报,2012,30(2):13-14.
[4] 薛定宇,陈阳泉.高等应用数学问题MATLAB求解[M].北京:清华大学出版社,2004.
[5] 曾庆山,曹广益,王振滨.分数阶PI^λD^μ控制器的仿真研究[J].系统仿真学报,2004,16(3):465-469.
[6] 王亚刚,许晓鸣.基于灵敏度的不稳定对象PID控制器[J].上海理工大学学报,2009,31(2):125-128.
(编辑:金 虹)
Fractional PID Control Applied to Excitation Control System
YULian-zhi, CHENGLing-ling
(College of Opitcal-electrical and Computer Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
In order to improce the dynamic and ststic performamces of the excitation control system and enhamce the ability of restraining disturbance,unadvisablc it is to use still the traditional PID controller for meeting the requirement,so new algorithms should be introdyced. The fractional order PID controller was proposed,in which two parameters more than the traditional PID controller can be regulated.The scope of controlling can be adjusted more widely and the controller can well meet the needs of the current excitation control system.The performance of the controller proposed was compared with that of the PID controller by simulations,The results show that the fractional order PID controller is superior to the traditional one.
excitation system;PID control;fractional PID control
TP 2
A
1007-6735(2013)04-0404-05
2012-08-15
于莲芝(1966-),女,副教授.研究方向:微小机器人技术及控制.E-mail:yulianzhi001@163.com
