双向不对等几何路径对卫星双向时间频率传递的影响

任烨，薛艳荣,3，李孝辉



双向不对等几何路径对卫星双向时间频率传递的影响

任烨1,2，薛艳荣1,2,3，李孝辉1,2

（1. 中国科学院国家授时中心，西安 710600；2. 中科院精密导航定位与定时技术重点实验室，西安 710600；3. 中国科学院大学，北京 100039）

分析了在卫星双向时间频率传递中，由地面站间钟差和卫星运动引起的双向几何路径不对等导致的双向几何路径时延差对双向时间比对计算结果的影响。选取了3颗卫星（中卫1号、北斗3G、IGSO70）和3组地面站（北京—成都、北京—喀什、北京—三亚）组成的9条卫星双向时间频率传递链路作仿真计算。对于这9条链路，仿真结果显示：1）当两地面站间钟差在1μs～10 ms范围内时，通过GEO卫星比通过IGSO卫星的双向不对等几何路径时延之差对双向时间比对计算结果的影响（值）较小；2）假设地面站间钟差在1ms内时，通过GEO卫星的卫星双向时间比对链路所对应的值均在皮秒量级，一般可忽略；通过IGSO卫星的卫星双向时间比对链路所对应的值均在纳秒量级，一般不可忽略。

不对等几何路径；卫星双向时间频率传递；钟差；卫星运动

0 引言

卫星双向时间频率传递是目前国际权度局（BIPM）进行国际时间比对所采用的主要技术之一。它是目前世界上最准确的远距离时间比对技术。目前，通过卫星双向时间频率传递技术，时间比对精度达0.3ns[1-3]。

在过去的一些分析计算中，将卫星双向时间频率传递的几何路径看作完全对等。但是，在实际情况中，卫星双向时间频率传递的几何路径通常不对等。本文研究在卫星双向时间频率传递中，由地面站间钟差和卫星运动引起的不对等几何路径导致的双向几何路径时延差对双向时间比对计算结果的影响。

1 基本原理

1.1 卫星双向时间频率传递的基本原理

卫星双向时间频率传递的原理[4-7]如图1所示。在地面站1使用调制解调器将本地原子钟的时间信号经伪随机码调制，通过甚小口径终端（VAST）将调制的扩频信号发射给卫星，经卫星转发器把站1的时间信号转发至地面站2，地面站2接收经卫星转发的地面站1的时间信号，解调信号后与地面站2的原子钟信号相比较。在地面站1发射信号的同时，地面站2以同样方式发射信号，地面站1接收其信号，并与本站原子钟信号相比较。通过两站数据交换，获得两地原子钟间的高精度钟差。

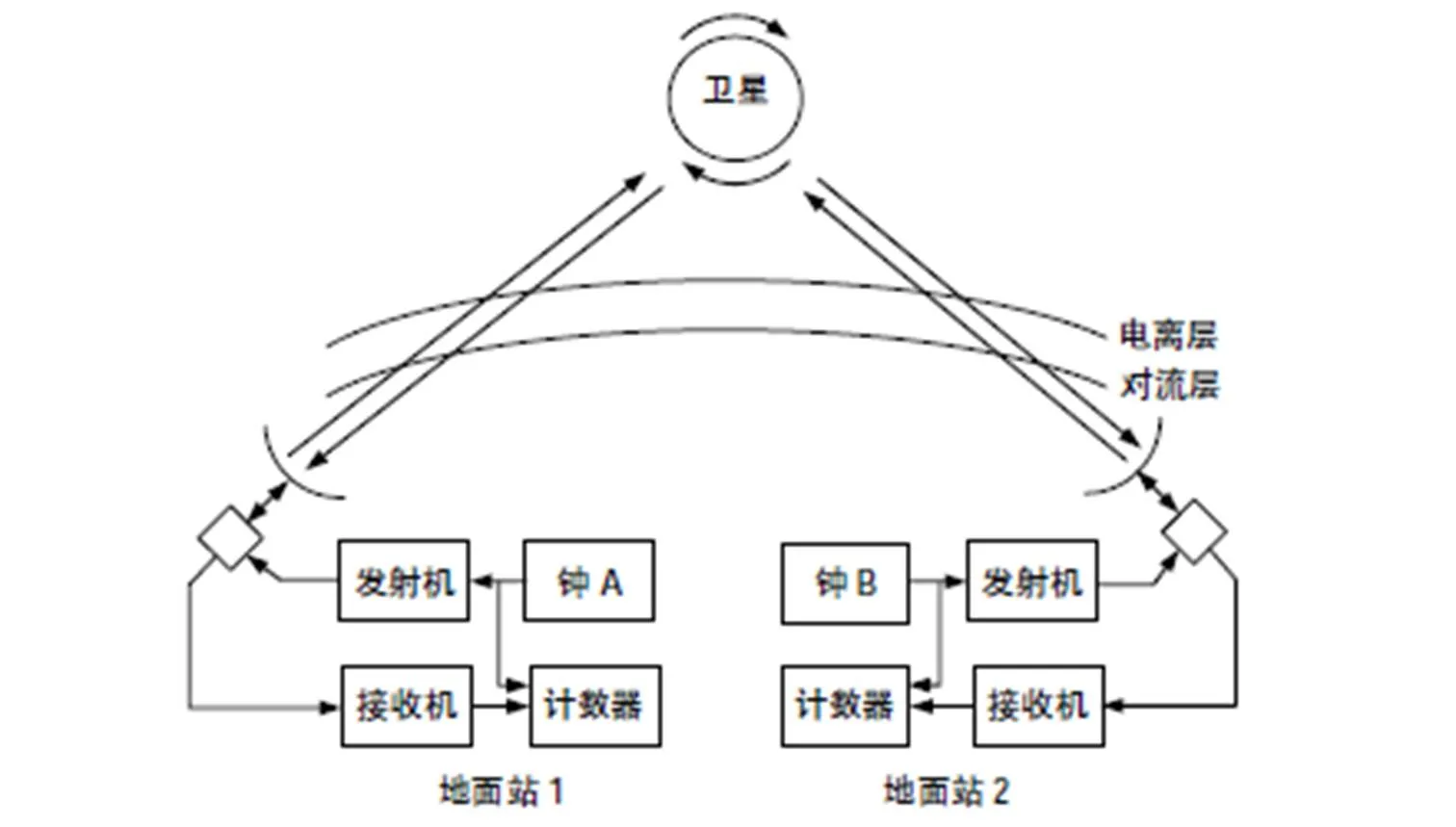
图1 卫星双向时间频率传递原理

下面介绍卫星双向时间频率传递在地面站1和地面站2间的时间比对关系。

地面站1的时间间隔计数器读数为

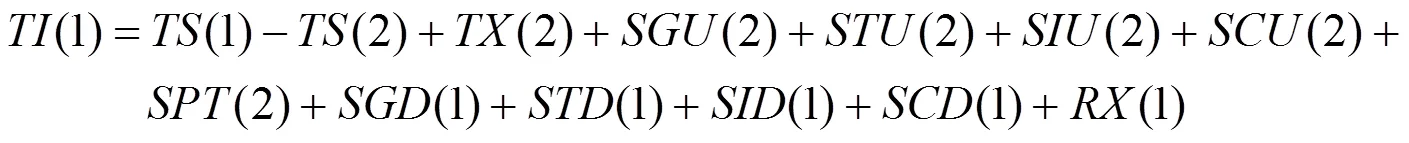
地面站2的计数器读数为

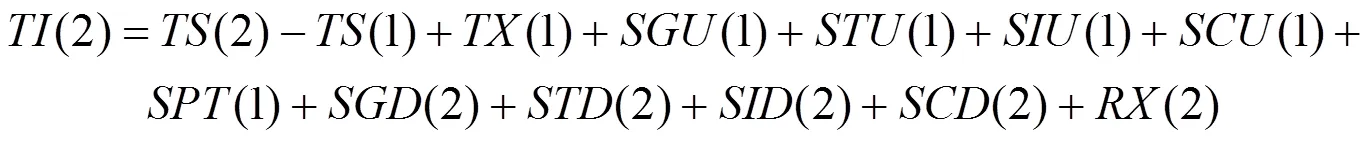
由（1）-（2），可得地面站1与地面站2的钟差：

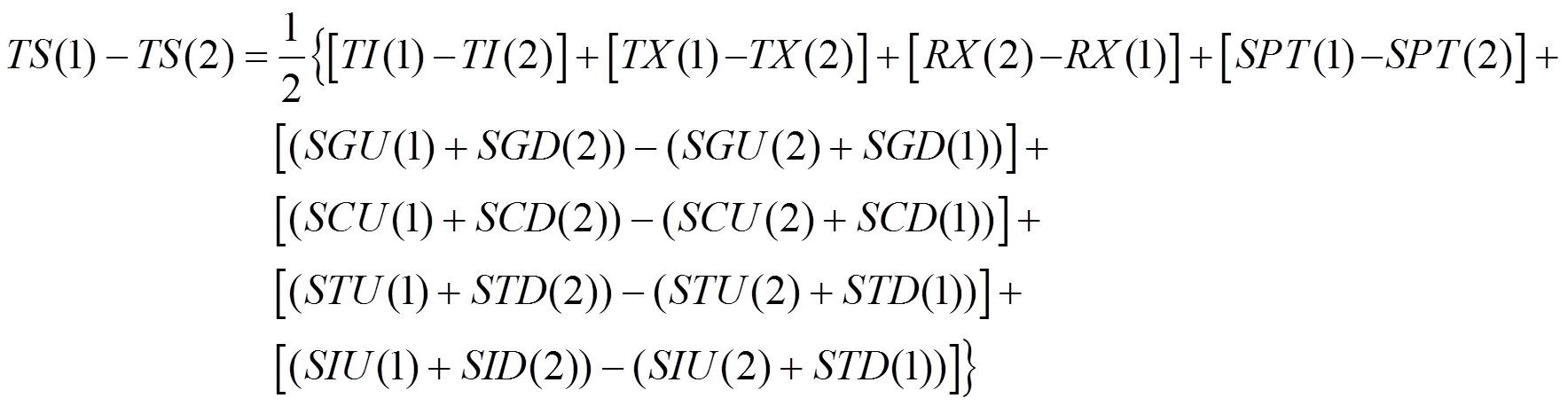
式（3）中，以方括号为单位，等号右边第1项为两站时间间隔计数器的读数差，第2项为地面站的仪器接收时延之差，第3项为地面站的仪器发射时延之差，第4项为卫星转发器时延之差，第5项为信号传递的几何路径时延之差，第6项为sagnac效应产生的信号传递时延之差，第7项为信号传递中的对流层时延之差，第8项为信号传递中的电离层时延之差。

1.2 双向不对等几何路径对卫星双向时间比对的影响基本原理

在实际情况中，卫星到地面站的距离通常不相等，同时，由于两地面站之间通常存在钟差，因此两地面站间不是严格同时发出信号的。因此，地面站发出的信号也不是同时到达卫星的。另外，在信号先后到达卫星的时间差内，卫星相对于地面站运动。如图2所示，由地面站1至地面站2之间的几何路径和由地面站2至地面站1之间的几何路径是不对等的，所以，由地面站1至地面站2的信号的几何路径时延与地面站2至地面站1的信号几何路径时延量不能完全抵消。由式（3）可知，这种双向几何路径时延差对双向时间比对计算结果的影响量可表达为

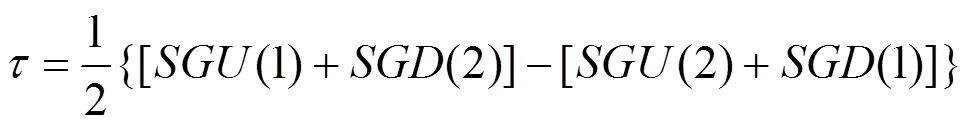
2 仿真实验

2.1 仿真方法

选取3颗卫星，其中2颗GEO卫星（中卫1号卫星、北斗3G）和1颗倾角为45°、升交点70°的IGSO卫星（IGSO70）；同时选取3组地面站（北京—成都、北京—喀什、北京—三亚）相应的9条双向时间频率传递链路。假设站间钟差分别在1μs，10μs，100μs，1ms，10 ms的情况下，选取1d的卫星星历数据（时间间隔为1 min）。其中，中卫1号卫星数据来自2004年10月5日转发式精密测定轨系统实测数据；IGSO70卫星数据来自倾角45°和升交点70°的模拟卫星轨道数据；北斗G1卫星数据来自2011年9月11日中国科学院国家授时中心实测的卫星轨道数据。基于以上卫星星历数据和时间频率传递链路，本文分析在两地面站与卫星之间距离不相等的情况下，在卫星双向时间频率传递的仿真实验中，双向几何路径时延差对双向时间比对结果的影响（值）。现以北京—成都两站间钟差为1μs，经中卫1号的卫星双向时间频率传递为例，计算双向不对等几何路径时延差对双向时间比对计算结果的影响。具体仿真步骤如下：

1）采用中卫1号卫星1d的星历数据（地心地固坐标系），数据之间的时间间隔是1 min。分别在地心地固坐标系中，对卫星位置的，，进行二次拟合；

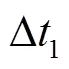
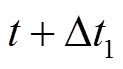
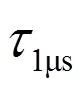
8） 重复步骤1）至步骤7），分别对北京—喀什、北京—三亚地面站间，分别经北斗3G卫星和IGSO70卫星的双向时间频率传递中，双向不对等几何路径时延差对双向时间比对计算结果的影响（值）进行仿真计算。

2.2 仿真结果

图3至图5分别显示了GEO卫星（中卫1号和北斗3G）和IGSO卫星（IGSO70）与北京地面站间的距离随时间的变化。同时，在双向时间频率传递中，当两地面站间的钟差分别为1μs，10μs，100μs，1 ms，10 ms时，并考虑卫星运动后，计算得到北京—成都之间双向不对等几何路径时延差对双向时间比对计算结果的影响，即式（4）所示的值，示于图6至图8；类似地，计算得到北京—喀什之间双向不对等几何路径时延差对双向时间比对计算结果的影响（值），示于图9至图11；计算得到北京—三亚之间双向不对等几何路径时延差对双向时间比对计算结果的影响（值），示于图12至图14。另外，表1与表2分别列出在3组地面站的钟差分别为1μs，10μs，100μs，1 ms，10 ms的情况下，分别经GEO与IGSO卫星的双向时间频率传递中，双向不对等几何路径时延差对双向时间比对计算结果的影响（值）。

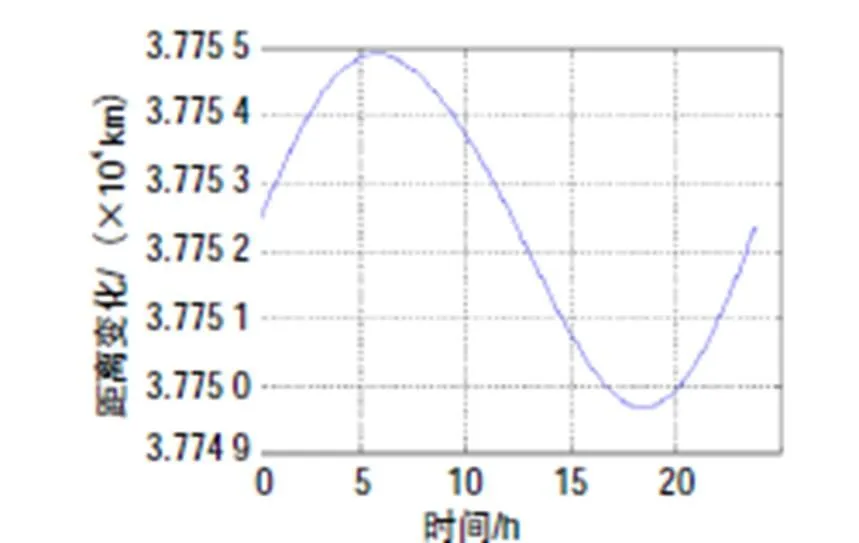
图3 北京到中卫1的距离随时间的变化

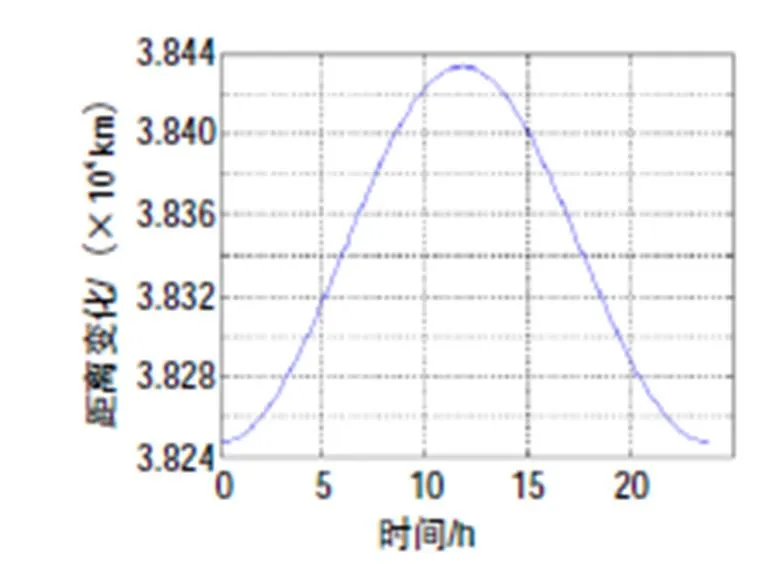
图4 北京到北斗3G的距离随时间的变化

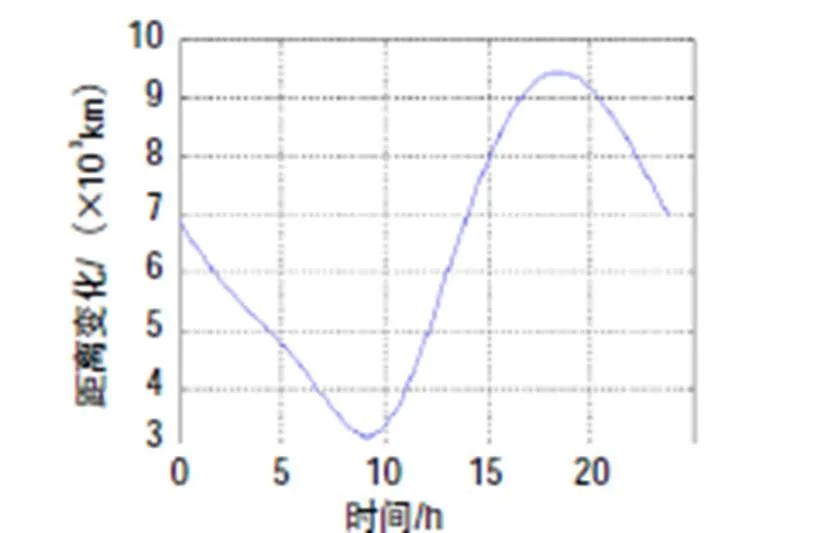
图5 北京到IGSO70的距离随时间的变化

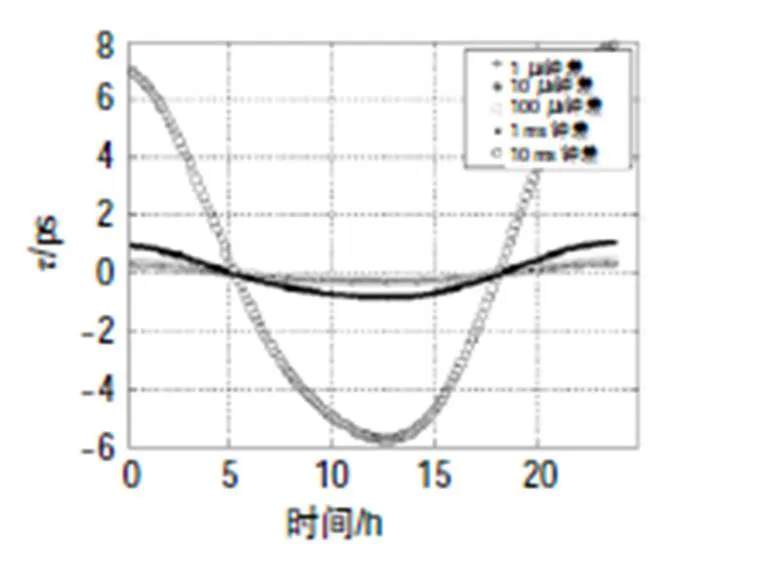
图6 经中卫1号卫星的北京—成都站间双向不对等几何路径时延差对应的值随时间的变化

图7 经北斗3G卫星的北京—成都站间双向不对等几何路径时延差对应的值随时间的变化

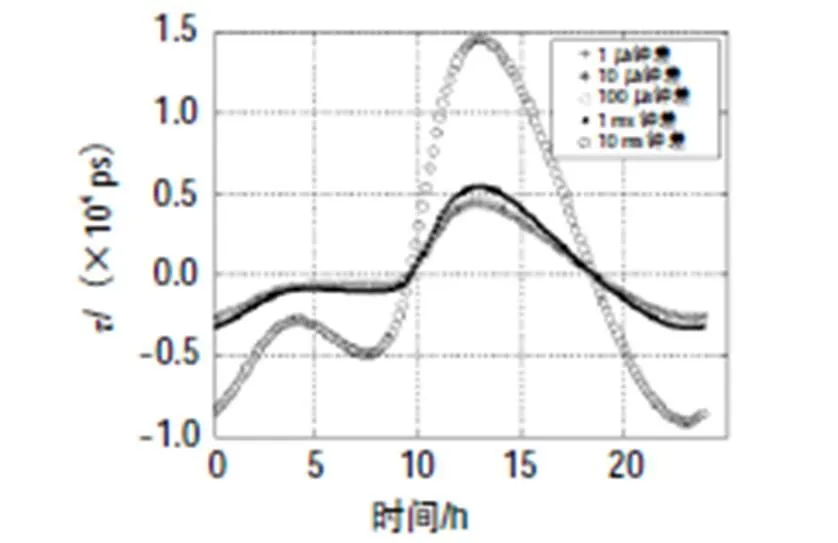
图8 经IGSO70卫星的北京—成都站间双向不对 等几何路径时延差对应的τ值随时间的变化

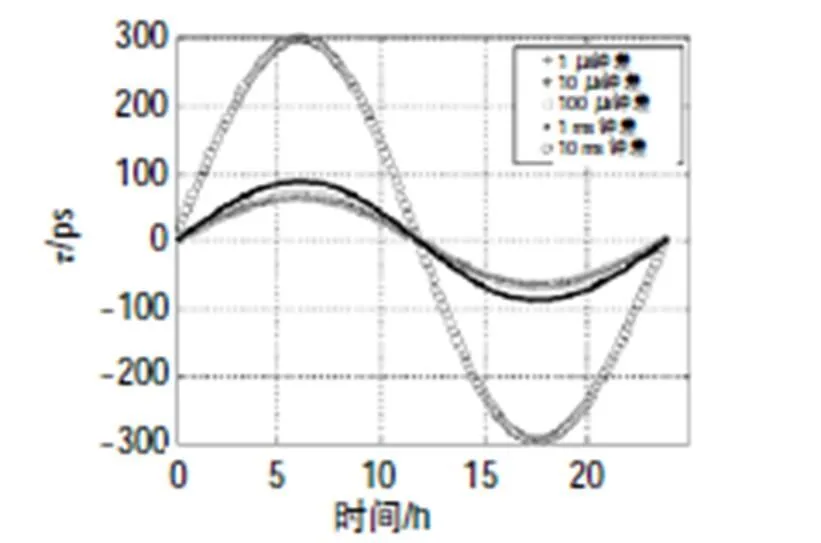
图10 经北斗3G卫星的北京—喀什站间双向不对 等几何路径时延差对应的τ值随时间的变化

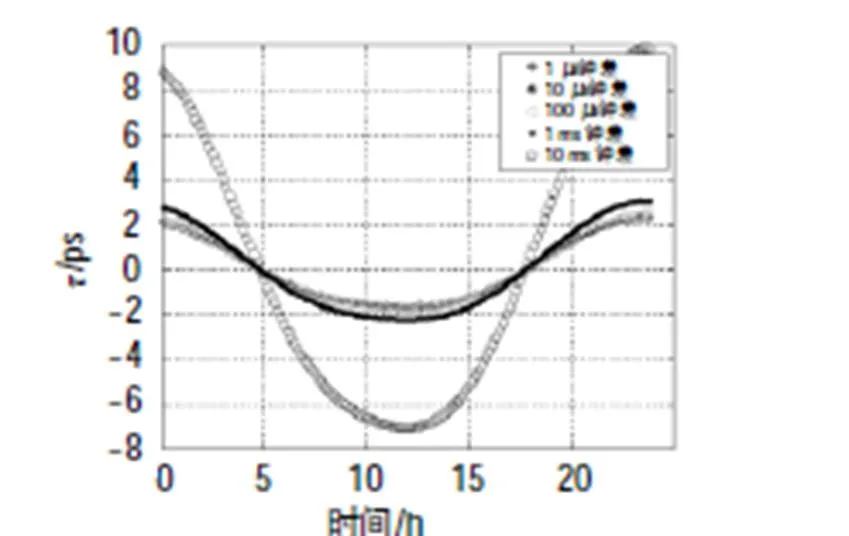
图12 经中卫1卫星的北京和三亚站间双向不对等几何路径时延差对应的值随时间的变化

图13 经北斗3G卫星的北京—三亚站间双向不对等几何路径时延差对应的值随时间的变化

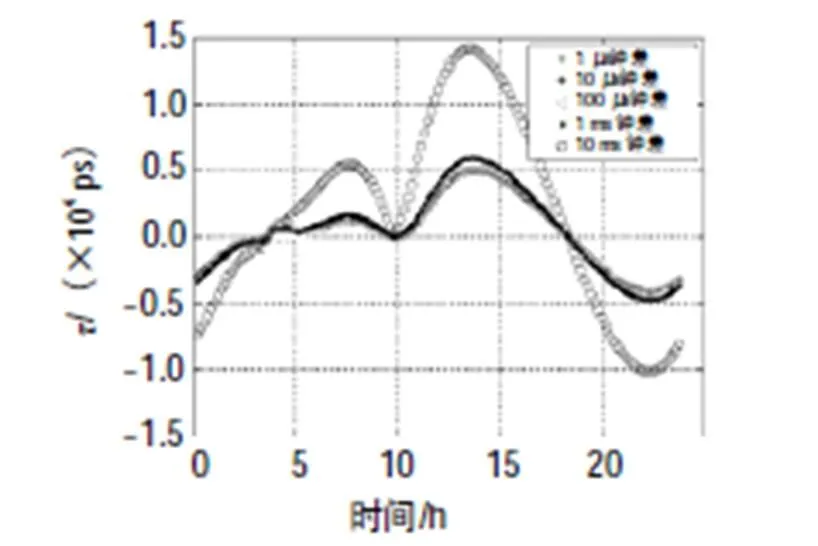
图14 经IGSO70卫星的北京—三亚站间双向不对 等几何路径时延差对应的值随时间的变化

表1 经GEO卫星的3组地面站间双向时间频率传递中，双向不对等几何路径时延差对应的值范围

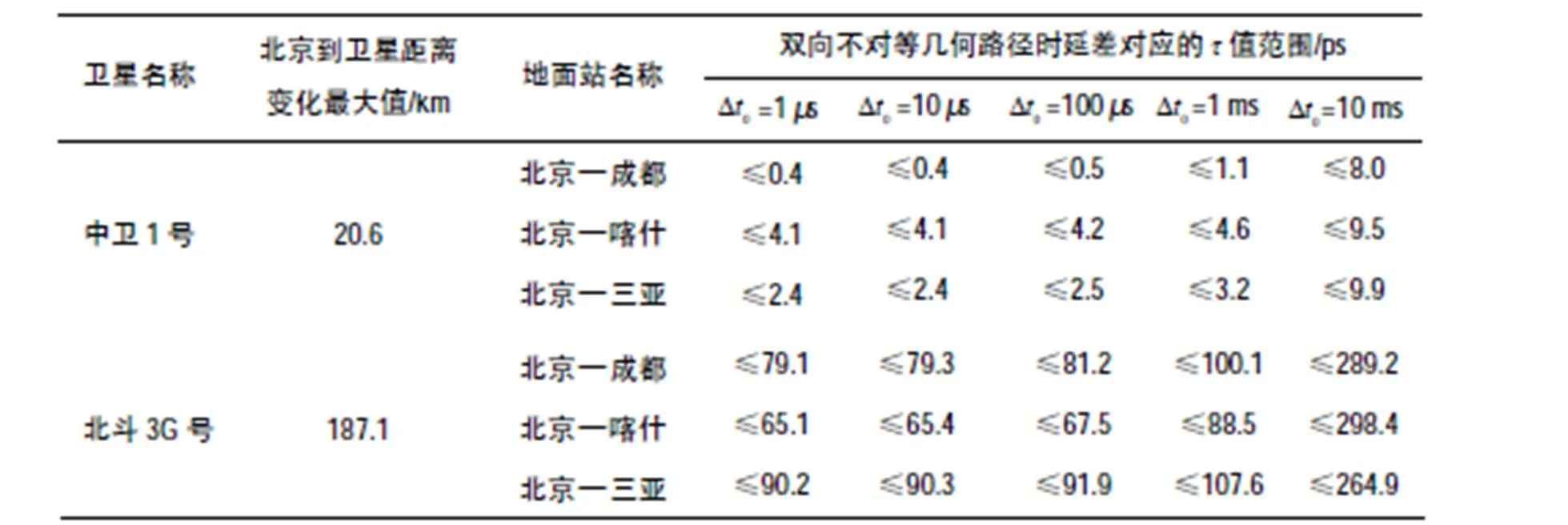
表2 经IGSO卫星的3组地面站间双向时间频率传递中，双向不对等几何路径时延差对应的值范围

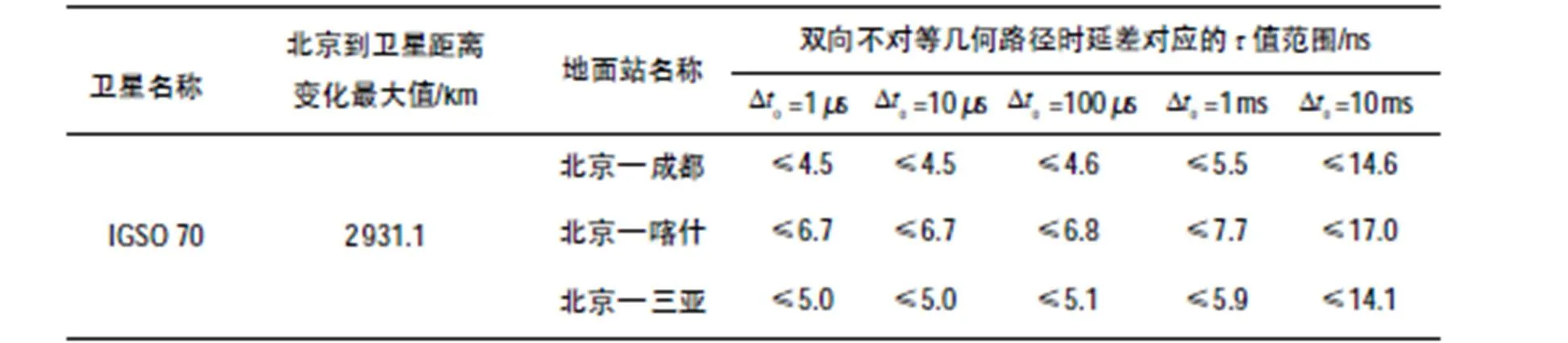
表1和表2表明，与经IGSO卫星的地面站间的双向时间频率传递相比，经GEO卫星的双向时间频率传递中，双向不对等几何路径时延之差对双向时间比对计算结果的影响（值）较小。其中，对经中卫1号卫星的双向时间频率传递而言，计算得的值在皮秒量级；对经北斗3G卫星的双向时间频率传递而言，计算得的值在亚纳秒量级；对经IGSO70卫星的双向时间频率传递而言，计算得的值在纳秒量级。另外，IGSO70卫星与北京之间距离随时间变化中的最大值（2 931.1 km）大于选取的2颗GEO卫星与北京之间距离随时间变化中的最大值（中卫1号为20.6 km，北斗3G为187.1 km）。

另一方面，由表1和表2可见，两地面站间的钟差越大，在卫星双向时间频率传递中，双向不对等几何路径时延差对双向时间比对计算结果的影响（值）也越大。计算表明，地面站间钟差为10 ms时，值随时间变化最大。图6至图14显示，假设当地面站间钟差在1ms内时，值均在纳秒量级，双向不对等几何路径时延差对双向时间比对计算结果的影响随时间变化的曲线几乎重合。

同时，在3组地面站中，北京—成都站间的双向不对等几何路径对应的值随时间的变化较小；北京—喀什站间的双向不对等几何路径对应的值随时间的变化较大。特别地，经北斗3G卫星的北京—喀什站间和北京—成都站间的双向不对等几何路径对应的值的最大值之间相差百倍。由此可知，值的大小与地面站间的距离有关系。

3 结论

考虑到地面站间钟差和GEO与IGSO卫星运动，本文分析了在卫星双向时间频率传递中，双向不对等几何路径时延差对双向时间比对计算结果的影响（式（4）所示的值）。对于本文涉及的9条链路，仿真结果表明：1）当两地面站间钟差在1μs～10 ms范围内时，通过GEO卫星比通过IGSO卫星的双向不对等几何路径时延之差对双向时间比对计算结果的影响（值）较小。2）假设地面站间钟差在1ms内时，通过GEO卫星的卫星双向时间比对链路所对应的值均在皮秒量级，一般可忽略；通过IGSO卫星的卫星双向时间比对链路所对应的值均在纳秒量级，一般不可忽略。

[1] 张虹, 李焕信, 李志刚. 双向卫星时间与频率传递温度效应[J].宇航计测技术, 2006, 26(1): 24-28.

[2] 周钰, 熊耀恒. 利用卫星进行双向时间传递[J].天文研究与技术, 2006, 3(1): 28-34.

[3] IMAE M, SUZUYAMA T. Two way satellite time and frequency transfer[J]. National Institute of Information and Communications Technology, 2003, 50(2): 125-133.

[4] JONG G. Precision of two-way international time scale comparisons[C]//Proc of the 6th European Frequency and Time Forum, 1992: 69-73.

[5] FRANKLIN G, ASCARRUNZ. Timing errors in two-way satellite time and frequency transfer using spread spectrum modulation[D]. USA: University of Colorado, 1999.

[6] BAUCHA , ACHKAR J, DACH R, et al. Time and frequency comparisons between four European timing institutes and NIST using multiple techniques[R]. Proceedings of the 2005 European Frequency and Time Forum, France: National Institute of Standard and Technology, 2005, 5: 101-109.

[7] 李志刚, 李焕信, 张虹. 卫星双向法时间比对的归算[J].天文学报, 2002, 43(4): 422-431.

Effect of two-way nonreciprocal geometric path on TWSTFT

REN Ye1,2, XUE Yan-rong1,2,3, LI Xiao-hui1,2

(1. National Time Service Centre, Chinese Academy of Sciences, Xi'an 710600, China; 2. Key Laboratory of Precision Navigation and Timing, National Time Service Centre,Chinese Academy of Sciences, Xi'an 710600, China; 3. University of Chinese Academy of Sciences, Beijing 100039, China)

The effect of the difference of the time delay, which results from the two-way nonreciprocal geometric path due to the clock offset between the two stations and the satellite motion, on the results of TWSTFT (two-way satellite time frequency transfer) is analyzed. A simulation is conducted for 9 links of TWSTFT, which relate to 3 satellites(chsat-1, BD-3G, IGSO70) and 3 pairs of station(Beijing—Chengdu, Beijing—Kashi, Beijing—Sanya). The simulation shows: 1)when the clock offset between the two stations is between 1 ms and 10 ms, the effect of two-way nonreciprocal geometric path via GEO satellite on the result of TWSTFT, i.e.value, is less than that via IGSO satellite; 2)when the clock offset between the two stations is less than 1 ms, the effect of two-way nonreciprocal geometric path via GEO satellite on the result of TWSTFT, i.e.value, is in the order of picosecond and can be ignored, while that for the path via IGSO satellite is in the order of nanosecond and final to be ignored.

nonreciprocal geometric path; TWSTFT; clock offset; satellite motion

P127.1

A

1674-0637(2013)04-0207-07

2012-08-23

国家自然科学基金重点资助项目（11033004）

任烨，女，硕士，实习研究员，主要从事时间频率测量方法研究。