一种基于改进Theta*的机器人路径规划算法

肖国宝，严宣辉

(福建师范大学数学与计算机科学学院，福建 福州 350007)

路径规划是智能交通、智能网络、机器人等人工智能研究领域的重要分支，所谓移动机器人路径规划技术，就是机器人根据自身传感器对环境的感知，在线规划出一条安全、可靠的运行路径，同时高效完成作业任务［1-2］.它是一个比较复杂的带约束条件的优化问题，约束条件包括但不限于:不与障碍物碰撞、运动路径最短、尽量远离障碍物、路径尽量平滑等［3-4］.

未知环境下的机器人路径规划是智能体实现其在线规划的前提，也是移动机器人导航中一个重要的问题.目前，确定性环境的导航控制方法已取得了大量的研究和应用成果［5-6］，在二维未知环境中的导航控制方面已展开了一些研究，并提出了若干方法［7-9］;但随着人类活动空间的扩张，已有的二维路径规划技术越来越满足不了许多领域的需求，人们迫切需要一套成熟可靠的三维空间路径规划技术［7］.

机器人路径规划需要考虑很多因素，其中主要包括环境的不确定性和动态特性、规划算法的优越性、实时能力等.三维环境下的机器人路径规划问题由于运动学和动力学约束变得非常复杂，机器人的自由度也大幅度增加，这要求规划算法的实时性要比较好，防止出现数据爆炸的情况.针对盲目搜索的效率较低，会耗费过多的计算空间与时间，目前用于三维路径规划比较常见的算法有 A*［8］、Diskstra、D*-lite、贪婪搜索、四/八叉树搜索［9］以及这些算法的改进［10-11］.采用的搜索策略如宽度优先、深度优先、启发式、非启发式搜索等［7］.

经典的启发式搜索算法——A*算法是由P.E.Hart等在20世纪60年代提出的，该算法在各个领域得到了广泛的应用［12］.A*算法也是目前用来解决游戏地图路径搜索问题最优的算法，但该算法只能用在格子环境中，这在一定程度上限制了其进一步的推广.Alex等在2007年提出了一种A*算法的变种——Theta*算法［13］，突破了格子的限制，允许以任意角度改变路径的方向.

启发函数是评定候选扩展节点的方法，以便确定哪个节点最有可能在通向目标的最佳路径上，它将会影响到整个算法的性能和效果.在大部分启发式搜索算法中的启发函数只估算到起始点和目标点的代价，没有合理地利用障碍物信息，这会限制其用于解决机器人路径规划问题时的进一步推广.

本文将局部环境的障碍物对机器人产生的斥力作为惩罚函数引入到启发函数中，为机器人提供了更加可靠的启发信息.首先，利用仿真实验的数据统计合理地选择惩罚函数权重，以确定启发函数;然后在此启发策略的基础上，改进A*算法的变种——Theta*算法，用PS_Theta*算法对路径进行平滑处理，优化路径.

1 算法描述

1.1 三维环境模型

移动机器人环境模型问题就是机器人根据传感器的感知获得环境的二维或三维空间模型.单元分解建模是典型的环境模型，其主要思想是将环境离散化为若干个规则的相同大小的基本单元——三维的立方格，通过二值信息便可以对障碍物和自由空间进行标识，因此使用简单的传感器即可获得创建地图的信息.然而，立方格的大小直接影响着移动机器人环境信息存储量的大小和规划时间的长短，立方格选得小，环境分辨率高，但环境信息存储量大，相应的干扰信号相对增加，使得决策工作量加大，最终导致规划速度变慢，降低系统的实时性;当立方格变大时，虽然抗干扰能力增强，但环境分辨率下降，在密集障碍物环境中不利于规划出有效的路径［14］.

在Matlab 7.6中建立2种常见的模型:1)城市环境模型，如图1;2)普通环境模型，如图2.其中，将机器人看作质点，不能碰到环境中的任何障碍物.

图1 城市环境模型Fig.1 Urban environment model

图2 普通环境模型Fig.2 Common environment model

任意时刻，在二维地图中，机器人的运动方向有8个，如图3所示，机器人可以到达相邻栅格的各个顶点;在三维地图中，机器人的运动方向有26个，如图4所示，机器人可以到达相邻立方格的各个顶点.

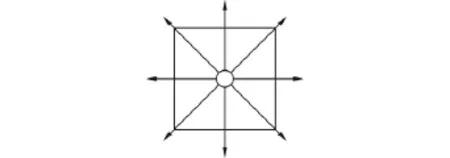
图3 二维运动方向Fig.3 The direction of movement in 2-D environment

图4 三维运动方向Fig.4 The direction of movement in 3-D environment

机器人路径规划问题就是在图中寻找一个从起始点S到目标点T之间点的集合，并要求相邻点之间的线段连接没有经过障碍物.

1.2 改进启发函数

在启发式搜索算法中，引入当前节点x的启发式估价函数f'(x)，其函数的定义式为

式中:f'(x)是从起点S出发到目标点的最小代价值f(x)的估价函数，g(x)是从起点S到当前节点x的实际代价值，h'(x)是从当前节点x到目标点估计的最小代价值，α、β是2个增益系数.显然，当h'(x)=0时，启发式搜索算法就变成了没有任何启发信息的盲目搜索算法，如普通Dijkstra算法.

在启发式搜索算法中，找到最优路径的关键在于估价函数h(x)的选取，如可以取两节点的欧几里德距离作为估价值.由式(1)可知，启发信息与环境中的障碍物无关，但对于机器人路径规划问题，障碍物的位置信息是规划过程中需要考虑的重要信息之一.因此，启发信息若能够考虑障碍物的位置信息将更有前瞻性和可靠性，有利于机器人准确地判断下一步的动作.在保证路径长度较短的前提下，尽可能地靠近目标点及远离障碍物是路径规划最理想的状态，此处引入人工势场法(artificial potential field，APF)的思想［15-16］，让机器人尽可能地避开障碍物.本文将一定范围内的障碍物对机器人产生的斥力作为一种惩罚函数添加至启发函数中.在人工势场法中斥力场公式为:

式中:η 是正增益系数;X=(xr，yr)和 XG=(xG，yG)分别表示机器人位置向量和目标点位置向量;ρ表示机器人到障碍物的欧式距离;ρ0表示单个障碍物影响的最大距离范围.相应的斥力为其负梯度，如式(2):

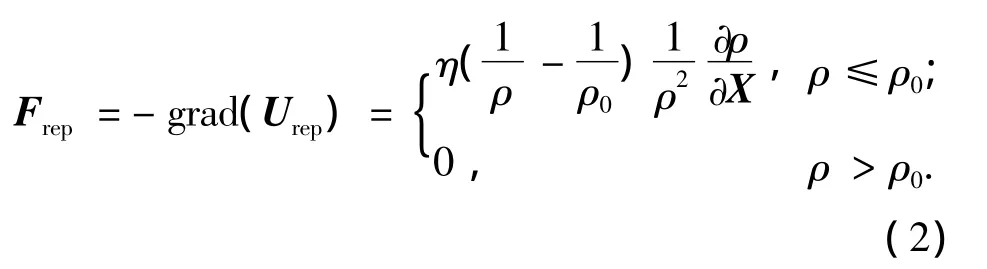
式中:

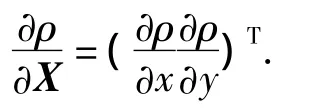
将式(2)作为惩罚函数可知，障碍物距离机器人越近，其产生的斥力就越大，进而相应的启发函数值也会增大，即惩罚越严重.将其并入到式(1)，得到式(3):

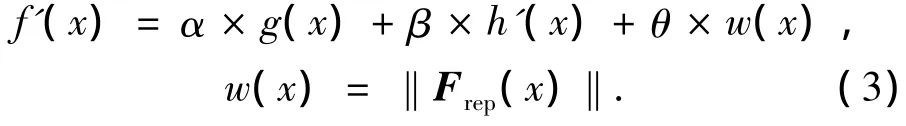
式中:g(x)是从起点S到当前节点x的实际代价值，h'(x)是从当前节点x到目标点估计的最小代价值(用与目标点之间的欧式距离来衡量)，w(x)是当前节点x在局部环境中所受到的斥力总和的模长，α、β、θ是3个增益系数.当 θ=0时，f'(x)为普通的启发函数，即与式(1)等价.

采用式(3)作为启发函数，考虑到了机器人从传感器得到的障碍物位置信息，可以根据局部环境信息的变化动态地修改启发函数，这将有利于规划出更优的轨迹.此外，经过改进的启发函数仍然能够满足启发式搜索算法的可归纳性［17］，即在一些问题的求解过程中，如果存在最短路径，无论在什么情况之下，该搜索算法都能够保证找到这条最短路径.

启发函数中的系数选择将会影响到函数的最终结果，从实验的角度分析系数的选择.选取α与β的最佳比例［18］为，β与θ最佳的比例从多个指标(路径长度、方向转换次数、扩展的节点数和运行时间)进行分析.在500×500的栅格中，采用具有代表性的启发式搜索算法——A*算法［12］作为测试算法，选择不同的β与θ比例在500种随机环境下进行路径规划，有效的平均数据统计如表1所示.

表1 不同增益系数比例下规划的数据统计结果Table 1 The calculation results of path planning in different gain factors

从表1的数据统计可以得出以下结论:1)采用同一比例的不同β与θ值规划后的轨迹基本一致;2)合理地将障碍物信息引入到启发函数后，可以得到更优的路径(当θ=0时，A*算法采用的是普通的启发策略);3)当比例大于10时，各项数据指标趋于稳定;4)从多个指标衡量，最佳的比例为(θ/β)=(1/7).同样，采用其他启发式搜索算法作为测试算法，其数据统计也能够反应出类似的趋势.

1.3 Basic Theta*算法及其改进

Basic Theta*算法是一种栅格路径规划算法，也是A*算法的一种变种，其最大的改进在于它不要求搜索树节点的父节点必须是其相邻的节点，因此所求解路径的轨迹不限制在栅格的横向与纵向，理论上允许以任意角度改变路径的方向［13］.

在估价函数的选取上，Basic Theta*算法与A*算法是一致的，故在使用其解决路径规划问题时，式(3)作为其启发函数能够获取更优的路径.该算法在搜索中设置了2个表:OPEN表和 CLOSE表.OPEN表保存了所有已扩展而未被考察过的节点，CLOSE表记录了已被考察过的节点.

Basic Theta*算法的步骤如下［19］.

1)初始化OPEN、CLOSE表，并将起始点S放入到OPEN表中.

2)如果OPEN表为空，表示没有找到路径，退出.

3)从OPEN表中找出最佳节点，作为当前节点x，并将其从OPEN表移到CLOSE表中.

4)判断当前节点x是否为目标点，如果是，则通过节点x的父节点，一直遍历到起点，找到路径的节点集合，搜索结束;否则，转至5).

5)开始扩展当前节点x，找到当前节点的所有后续节点集合U并遍历集合内节点.如果遍历的节点yi不在OPEN或者CLOSE表中，将该节点yi加入OPEN表中，计算该节点yi的估计值，并记录其父节点为x;否则，转至6).

6)判断当前节点x的父节点x'与遍历的节点yi是否相通(节点之间的线段没有经过障碍物):

①若相通，比较当前节点的父节点x'的代价g(x')和OPEN表中的代价g(yi)，如果g(x')较小，则更新表中的代价，并将节点yi的父节点指向x';

②若不相通，直接比较当前节点的代价g(x)和OPEN表中的代价g(yi)，如果g(x)较小，则更新表中的代价及父节点.

7)按照估价值递增顺序，对OPEN表中的节点进行排序，转向2).

Basic Theta*算法能够突破格子的限制，找到可行路径，但该算法存在着一些缺陷，即最先找到的路径并不能保证路径最短.如图5所示，最短路径应该是E1到B9的线段，但E1不会成为B9的父节点，路径经过了点C6.分析其原因在于Basic Theta*的扩展方式［13］，即2个顶点之间并不会随意形成父节点与子节点的关系.

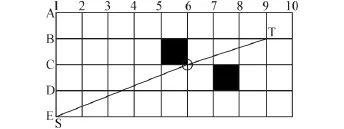
图5 Theta*算法规划轨迹演示Fig.5 The path planning demo of Theta*algorithm

对路径进行平滑处理能够有效地优化路径［20］，在经过Basic Theta*算法搜索找到路径后，中间经过的点会大量减少，对其进一步平滑可以在较短的时间内完成.具体平滑步骤如下.

1)获取Basic Theta*规划后的路径轨迹节点集合.

2)选择集合中的起始点为平滑的基准点x.

3)判断节点x与节点z是否相通，其中，节点z为节点y的后续节点，节点y为节点x的后续节点:

①若相通，去除中间节点y，即将节点x的后续节点修改为节点z，相应地，节点z的父节点为节点x;

②否则，将基准点更新为节点y.如此循环，直到节点y为目标点时，循环结束，转到4).

4)平滑完毕后，从目标点回溯到起始点，重新组成最佳的节点集合.

由Basic Theta*算法与平滑步骤组成PS_Theta*算法，针对图5中Basic Theta*算法规划的轨迹，PS_Theta*算法能够进一步优化路径，如图6所示.光滑度是路径轨迹优越性的重要指标，光滑的轨迹能够有效提高机器人到达目标点的效率，可以尽可能地满足非完整性约束的条件.

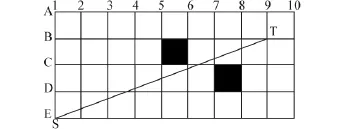
图6 PS_Theta*算法规划轨迹演示Fig.6 The path planning demo of PS_Theta*algorithm

2 仿真与结果分析

2.1 二维随机环境下的路径规划问题

本文在Matlab 7.6环境下对算法进行验证和比较.在二维环境下，采用本文提出的改进启发式搜索策略，对 A*［12］、Basic Theta*［13］与 PS_Theta*算法进行对比实验.在栅格模型中，选择2种规格进行测试，分别为100×100与500×500，障碍物按不同比例随机生成，并随机初始化起始点与目标点，统计500次仿真实验，平均数据如表2所示，图7和8分别表示2种规格下3种算法规划的平均路径方向变化频率曲线图.

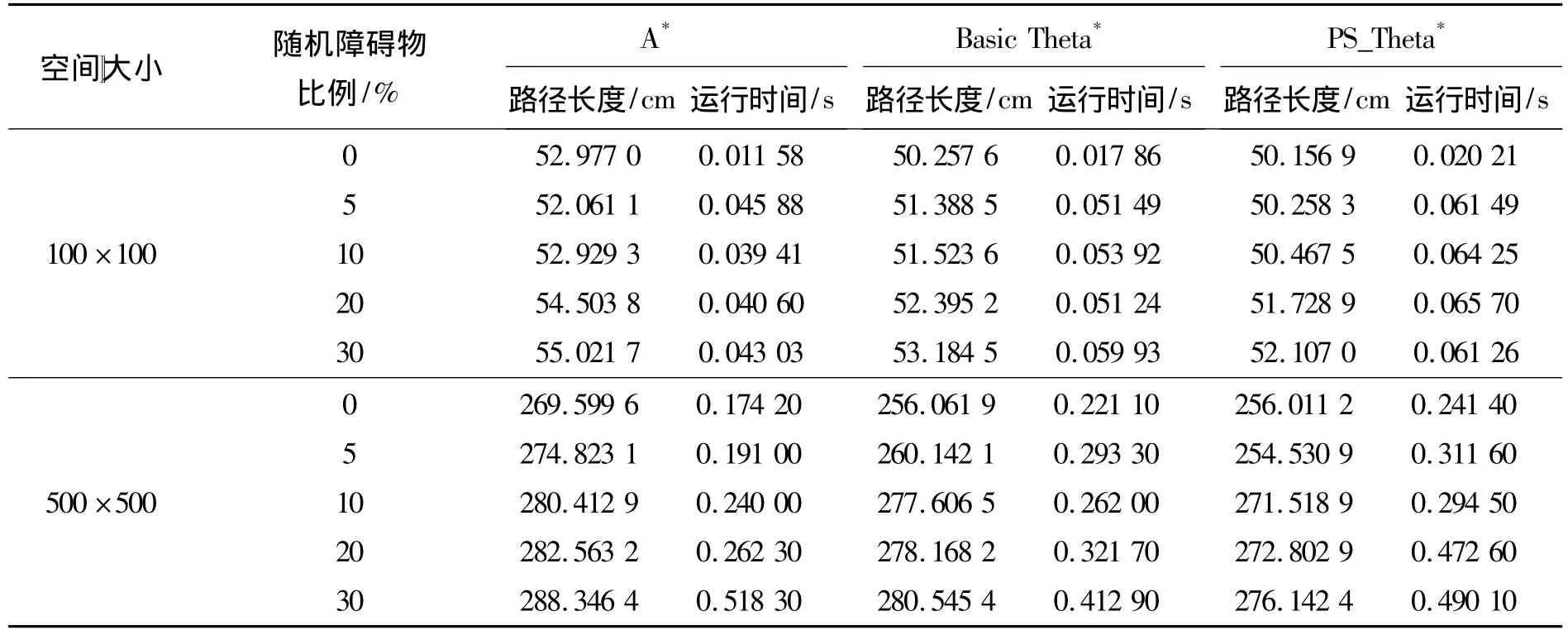
表2 二维随机环境的仿真实验结果Table 2 The simulation experimental results in 2-D random environment

图7 路径方向变化频率曲线(100×100)Fig.7 The graph of heading changes(100 ×100)

图8 路径方向变化频率曲线(500×500)Fig.8 The graph of heading changes(500 ×500)

由表2的数据及图7和8的曲线图可以表明，使用Basic Theta*算法能够规划出较短的路径，PS_Theta*算法利用较少的额外运行时间代价使得路径更优，主要体现在2点:1)路径长度更短;2)路径方向变化大量降低.路径方向变化频率能够体现路径的光滑程度，是路径优越性的重要指标.

2.2 三维随机环境下的路径规划问题

将采用启发式搜索算法解决路径规划问题的环境规模扩展至三维随机环境中.在2种环境模型下采用不同启发式搜索算法进行路径规划，2种随机的城市环境模型的规划轨迹如图9和10所示，从多个角度观察普通环境模型的规划轨迹如图11和12所示.3种启发式搜索算法均能够快速地找到目标点，从规划后的对比效果可以表明，PS_Theta*算法规划的路径轨迹长度最短.

图9 城市环境模型规划演示1Fig.9 Urban path 1

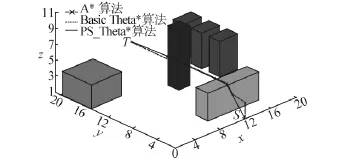
图10 城市环境模型规划演示2Fig.10 Urban path 2

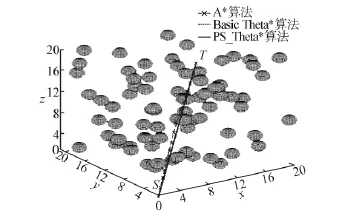
图11 普通环境模型规划结果Fig.11 The path 1 in common environment

图12 普通环境模型规划结果Fig.12 The path 2 in common environment

最后，通过多次实验的统计数据对比算法的性能.在三维立方格模型中，选择2种规格进行测试，分别为50×50×50与100×100×100，按不同比例随机生成障碍物，并随机初始化起始点与目标点的位置.统计500次仿真实验，平均数据如表3所示，图13和14分别表示2种规格下3种算法规划的平均路径方向变化频率曲线图.

图13 路径方向变化频率曲线(50×50×50)Fig.13 The graph of heading changes(50 ×50 ×50)

图14 路径方向变化频率曲线(100×100×100)Fig.14 The graph of heading changes(100×100×100)

表3 三维随机环境的仿真实验结果Table 3 The simulation experimental results in 3-D random environment

由表3的数据及图13和14的曲线图可以表明，在三维随机复杂的环境下，3种启发式搜索算法均能够快速地找到路径.相比其他2种算法，PS_Theta*算法利用较少的额外时间代价，大幅度降低了路径方向改变的频率，保证了轨迹的平滑性，并且能有效地缩短路径长度.相比二维环境，PS_Theta*算法的优势更加明显，提高了路径方向变化的区分度.

3 结束语

启发式搜索是一种有序高效的搜索策略，其相对简单的时间复杂度能够保证规划的实时性，本文将障碍物对机器人产生的斥力作为惩罚函数加入到启发函数中，合理性主要体现在以下3点:1)提高启发函数的前瞻性与可靠性;2)考虑到了障碍物对机器人的影响，能够较好地选择节点，减少扩展的节点数量;3)有效地减少规划时间，提高效率.而将Theta*算法应用在三维随机环境解决机器人路径规划问题，相比A*算法，体现出了其算法的优越性，即有效缩短了路径长度.利用改进算法PS_Theta*对路径进行平滑处理，能够大幅度地降低路径方向变化的频率，提高轨迹的平滑性.

总之，将局部环境中的障碍物信息引入到启发函数中，为机器人提供更加可靠的启发信息，以提高其下一步动作的准确性，使用改进算法大幅度降低了规划的路径方向变化，这在实际应用中能够提高机器人动作连贯性，加快到达目的地.

［1］朱大奇，颜明重.移动机器人路径规划技术综述［J］.控制与决策，2010，25(7):961-967.ZHU Daqi，YAN Mingzhong.Survey on technology of mobile robot path planning［J］.Control and Decision，2010，25(7):961-967.

［2］肖国宝，严宣辉.一种动态不确定环境中机器人路径规划方法［J］.计算机系统应用，2012，21(4):92-98.XIAO Guobao，YAN Xuanhui.Path panning of mobile robot in dynamic nondeterministic environments［J］.Computer Systems and Applications，2012，21(4):92-98.

［3］张捍东，郑睿，岑豫皖.移动机器人路径规划技术的现状与展望［J］.系统仿真学报，2005，17(2):439-443.ZHANG Handong，ZHENG Rui，CEN Yuwan.Present situation and future development of mobile robot path planning technology［J］.Acta Simulata Systematica Sinica，2005，17(2):439-443.

［4］刘华军，杨静宇，陆建峰，等.移动机器人运动规划研究综述［J］.中国工程科学，2006，8(1):85-94.LIU Huajun，YANG Jingyu，LU Jianfeng，et al.Research on mobile robots motion planning:a survey［J］.Engineering Science，2006，8(1):85-94.

［5］禹建丽，李晓燕，王跃明，等.一种基于神经网络的机器人路径规划算法［J］.洛阳工学院学报，2001，22(1):31-34.YU Jianli，LI Xiaoyan，WANG Yueming，et al.An algorithm of path planning for car-like robots based on neural network［J］.Journal of Luoyang Institute of Technology，2001，22(1):31-34.

［6］HU Yanrong，YANG S X.A knowledge based genetic algorithm for path planning of a mobile robot［C］//Proceedings of the 2004 IEEE International Conference on Robotics and Automation.New Orleans，USA，2004:4350-4355.

［7］陈洋，赵新刚，韩建达.移动机器人3维路径规划方法综述［J］.机器人，2010，32(4):568-576.CHEN Yang，ZHAO Xin'gang，HAN Jianda.Review of 3D path planning methods for mobile robot［J］.Robot，2010，32(4):568-576.

［8］SATHYARAJ B M，JAIN L C，FINN A，et al.Multiple UAVs path planning algorithms:a comparative study［J］.Fuzzy Optimization and Decision Making，2008，7(3):257-267.

［9］WU X J，TANG J，LI Q，et al.Development of a configuration space motion planner for robot in dynamic environment［J］.Robotics and Computer-Integrated Manufacturing，2009，25(1):13-31.

［10］CARSTEN J，FERGUSON D，STENTZ A.3D field D:improved path planning and replanning in three dimensions［C］//2006 IEEE/RSJ International Conference on Intelligent Robots and Systems.Beijing，China，2006:3381-3386.

［11］DOLGOV D，THRUN S，MONTEMERLO M，et al.Practical search techniques in path planning for autonomous driving［C］//Proceedings of the First International Symposium on Search Techniques in Artificial Intelligence and Robotics.Chicago，USA，2008:1-6.

［12］HART P E，NILSSON N J，RAPHAEL B.A formal basis for the heuristic determination of minimum cost paths［J］.IEEE Transactions on Systems Science and Cybernetics，1968，4(2):100-107.

［13］NASH A，DANIEL K，KOENIG S，et al.Theta*:anyangle path planning on grids［C］//Proceedings of the Twenty-Second AAAI Conference on Artificial Intelligence.Vancouver，Canada:AAAI Press，2007:1177-1183.

［14］蔡自兴，徐光祐.人工智能及其应用［M］.3版.北京:清华大学出版社，2004.

［15］SABATTINI L，SECCHI C，FANTUZZI C.Arbitrarily shaped formations of mobile robots:artificial potential fields and coordinate transformation［J］.Autonomous Robots，2011，30(4):385-397.

［16］SHENG Junwen，HE Gaoqi，GUO Weibin，et al.An improved artificial potential field algorithm for virtual human path planning［C］//Proceedings of the Entertainment for Education，and 5th International Conference on E-learning and Games.Berlin/Heidelberg，Germany:Springer-Verlag，2010:592-601.

［17］周小镜.基于改进 A*算法的游戏地图寻径的研究［D］.重庆:西南大学，2011:22-23.ZHOU Xiaojing.Research of routing in the game map based on improved A*algorithm［D］.Chongqing:Southwest University，2011:22-23.

［18］De FILIPPIS L，GUGLIERI G，QUAGLIOTTI F.Path planning strategies for UAVS in 3D environments［J］.Journal of Intelligent＆ Robotic Systems，2011，65(1/2/3/4):247-264.

［19］NASH A，KOENIG S，LIKHACHEV M.Incremental Phi*:incremental any-angle path planning on grids［C］//Proceedings of the 21st International Joint Conference on Artificial Intelligence.San Francisco，USA:Morgan Kaufmann Publishers Inc.，2009:1824-1830.

［20］BOTEA A，MULLER M，SCHAEFFER J.Near optimal hierarchical path-finding［J］.Journal of Game Development，2004，1(1):7-28.