双轮铣槽机泥浆管内部流体流态分析与模拟
2013-06-18李万莉
李万莉,谭 祺
LI Wan-li,TAN Qi
(同济大学 机械与能源工程学院,上海 200092)
双轮铣槽机作为一种国内新兴的连续墙挖掘设备,以其挖掘深度大,垂直精度好,作业效率高等优点正在成为连续墙施工领域的主要装备。设备主要包括铣削斗体,起重设备和泥浆处理设备。铣削斗体上有两个铣轮用于铣碎地层,通过泥浆管将铣削产生的沙石运达泥浆处理设备进行滤渣并回灌浆体护壁。
为了适应斗体深度的不断改变,起重设备上设有软管卷盘,缠绕着泥浆管来控制泥浆管的伸出长度使其保持绷直(图1);由于铣削斗体的工作深度可达100m 甚至更大,斗体内的泥浆泵必须提供足够的压力来保证泥浆能够通过管道运达泥浆处理设备。软管卷盘如图1 所示,其软管经过缠绕后形成了螺旋线,内部两相流的流场相比于直线管道变得更为复杂,压力损失增大,对于泥浆泵的要求也随之升高。

图1 双轮铣软管卷盘及软管示意图
故本文着眼这段复杂流型的两相流流体,对其成分组成、参考模型和流动状态进行分析,并使用流体模拟软件进行模拟,对比在不同流速和深度下的管内压力损失,为实际泥浆泵的功率分配控制提供方法参考和数据借鉴。
1 两相流模型
目前使用最广泛的固液两相流模型是连续介质模型。连续介质理论的基本思想是假设固相和液相都是连续的,其各相的质点可同时占据相同的空间位置,各相也就具有各自的压力、速度、温度的分布。如果选取其中一项作为控制体,那么其内部的动力特性可以用单项介质的方程来描述,而只是在其边界处与其他相发生作用。
1.1 控制方程
对于任意的某相介质k,总控制方程为

式中 k—相数,k=l(或s)代表液(或固)相;
ψk—k 相的某一流动参数;
ρk—k 相的密度;
uk—k 相的速度;
Jk—k 相的面通量;
φk—单位质量的源相。
总控制方程中的4 项依次代表瞬态项、对流项、扩散项和源项,对该方程中的各个参数不同取值后,就能得到质量、动量以及能量3 个守恒方程。当然,如需使控制方程封闭,还需诸如热力学状态方程、应力方程和能量方程这些本构方程[1]。
1.2 模型选择
对于已经确定了的控制方程,两相流问题所涉及的参、变量仍十分复杂,待求数目众多,所建立的微分方程组很难找到精确的解析解,所以一般理论分析的过程是,在建立方程组的基础上给定初值进行迭代,直至变量收敛到一定精度为止;同时,在研究过程中还会作进一步的假设,建立简化模型来求解方程。
联系双轮铣的具体工况,工作装置作用在地下,通过泥浆管把铣削产生的颗粒运至地面,整个过程是固体物料的水力输送过程,具体施工时会通过在泥浆中添加膨润土来提高携渣能力,故携带的泥沙含量普遍较大,固液两相流中的颗粒体积浓度超过0.4%,可视为密相流动。学者魏家进曾专门对于此类流体建立了密相液固两相k-ε-T 湍流模型[2]。该模型基于下列4 项假设:①流体相和颗粒相均视为连续介质;②颗粒为大小均匀的球形且无破碎;③流动定常且无质量交换;④颗粒与流体之间主要存在粘性拖曳力和相间压力作用。这些假设有助于简化方程组,同时又比较能够满足泥浆泵吸系统实际工作时泥浆两相流的流动状态。
2 软件模拟
随着计算机技术的不断提升以及诸如有限体积法、有限差分法等合适的计算方法的发展,基于数值计算的计算流体力学正越来越多地运用到工程和研究中。
所谓的数值方法的实质是离散化和代数化,通过网格划分将原本的偏微分方程离散,用节点或中心处的变量值来近似描述原微分方程中的关系,构造出离散的代数方程组,在给定初值的基础上迭代求解,近似表示流场内各变量的分布情况。
2.1 模型建立
为了模拟双轮铣实际工作状态,在建模时选定泥浆软管的外径为230mm,内径为150mm,总长较实际短,为13.15m。双轮铣泥浆管实际状态下会呈现螺旋状和直线状这两种排布方式,所建立的模型在总长度相同的情况下,调整直管和螺旋管的长度分配,以模拟当铣削斗体改变深度时泥浆软管随之发生的排布变化,3D 模型如图2 所示,模型的具体参数如表1。

图2 流体模型对比
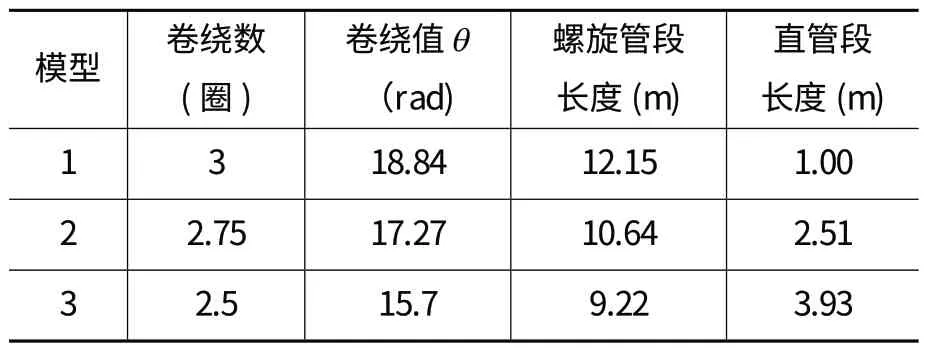
表1 模型的外部尺寸
其中螺旋管段的轴线为阿基米德螺旋线,计算获得软管长度和缠绕角度(弧度值)之间的关系
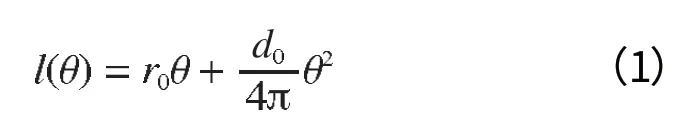
2.2 网格划分
将上述模型以.x_t 格式导入ANSYSWORKBENCH 中的FLUENT 流体计算模块,使用ICEM_CFD 进行网格划分。以模型1为例,使用非结构化网格划分方法,网格类型为四面体网格,计算机求解后获得网格总数约23 万。
2.3 条件设定
在FLUENT软件中导入完成网格划分的.msh文件,检测网格质量后开始设置模拟参数。采用欧拉多相流模型,相数为2,主要相为液态水,次要相为砂粒。
在双轮铣的工作过程中,铣削斗体的工作深度不断变化,泥浆泵吸入泥浆的组分和浓度也会不断改变,所以软管的边界条件并不唯一。故在模拟中,选取进口速度从1m/s 至3m/s 每隔0.5m/s 依次改变,同时改变砂粒的体积浓度为1%、5%和20%;出口设置为压力出口,压力值为1 个大气压。使用以上参数设置分别对3 个模型进行模拟。
3 模拟结果与分析
3.1 压力场分布
模拟计算完成后,可得到相应流体压力云图。总结压力的分布状况如下:直管段沿重力方向有明显的压力梯度;进入螺旋管段后,沿着流向的压力梯度不再呈一致递减的趋势,下部的管段的压力会高于之前上部管段的压力,但压力随流向总体上有减小趋势,这产生的原因是:流体在螺旋管段上下来回流动,位能和动能相互转化,压力方面的位能损失产生周期性变化;而螺旋管段两端口的高度差其实很小,最终总位能损失可以忽略,由于管道摩擦、颗粒碰撞等导致的能量损失却始终增大,致使总压力趋势减小。
3.2 压力损失
从模拟结果中获取整段流体的入口压力(以在入口速度3m/s,颗粒体积浓度0.2,粒径0.5mm 边界条件为例,其入口压力约为1.23MPa),计算其与出口压力的差值得到总压力损失。图3~图5是3个模型分别在不同入口速度和颗粒浓度下的压力损失折线图,从图中可得出规律:①输送的颗粒浓度对压力损失有较大的影响,浓度越高,损失越大;②随着流体入口速度的增加,压力损失增大,且在不同浓度的情况下,压力梯度的变化趋势相近;③在入口速度较低而浓度较大时,随着入口速度的减小,压力损失反而有所增大。
两相流的压力损失由众多的因素造成,除了流形不同所造成的损失外,两相流压力损失主要来源于提升流体产生的位能损失、流体与管壁产生的摩擦损失、颗粒间和颗粒管壁相互碰撞产生附加压力损失。几种损失叠加可得总压力损失。
位能损失和流体密度有直接关系,随着两相流颗粒浓度的增大而增大;摩擦损失受流体速度影响,流速越快损失越大;当流速较低、浓度较大时,摩擦损失对总体损失的贡献变小,相反流体中的固体颗粒产生碰撞的概率变大,碰撞所引起的附加压力损失增大。
另外,两相流的压力损失还会受到流形,即软管排布方式的影响,螺旋管段与直管段的主要不同在于:螺旋管段内流形复杂,局部压力损失较大,位能损失可以忽略,直管段与之相反。
图6 将模型一和模型三的压力损失进行作差对比,发现在相同总长的前提下,垂直管段所占比例更大的模型三在相同条件下有着更大的压力损失,可见在模拟所设定的条件下,位能损失对于总压力损失的影响较大。
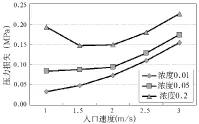
图3 模型一流体速度与压力损失关系
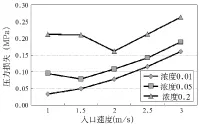
图4 模型二流体速度与压力损失关系
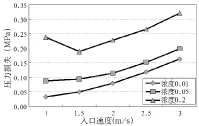
图5 模型三流体速度与压力损失关系
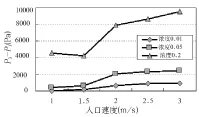
图6 模型一、三压力损失比较
3.3 泥浆泵控制
结合以上模拟所得的两相流压力损失变化,可得到以下关于泥浆泵的控制规律。
1)控制泥浆泵的转速,使泥浆流速保持在最优工作范围。即避免流速过大使摩擦损失增大、流速过小时又导致颗粒频繁碰撞,附加的压力损失过大。
2)大深度作业阶段,应当设置泥浆泵最低获取功率值。大深度时地层坚硬,发动机功率一般优先分配给铣轮,但这时泥浆的位能损失同样可观,在此类情况下设定泥浆泵最低获取功率值对双轮铣安全运行起到保障作用。
4 小 结
本文首先介绍泥浆两相流模型,然后基于FLUENT 模拟软件,参照双轮铣槽机泥浆软管内的两相流流体建立3 个模型,模型总长相同但垂直管段和螺旋管段占比不同,进而着眼流体的压力损失进行了模拟,得到在不同流速和浓度下的压力云图,获取压力损失梯度之后进行对比分析,最后探讨了造成压力损失的原因并结合铣槽机工况提出了一些泥浆泵的控制规律,对于双轮铣泥浆泵的选型和控制提供借鉴和参考。
[1]岳湘安.液—固两相流基础[M].北京:石油工业出版社,1996.
[2]魏进家,胡 春,姜培正,等.密相液固两相湍流K-ε-T 模型及其在管道两相流中的应用[J].应用数学和力学,2000,21(05):468-476.
[3]夏建新,倪晋仁,黄 家,等.锰结核在垂直管路输送过程中的压力损失[J].泥沙研究,2002,(02):23-28.
