大型圆环导轨平面度测量方法及在实际测量中的应用

江苏新瑞重工科技有限公司 （常州 213166） 朱红卫 尤敏志

大型回转类零件圆环导轨平面度的测量方法较为复杂，在实际生产中大型圆环导轨也较为少见。本文就公司一台LMV600车铣复合加工中心在生产制造中对其转台上圆环导轨平面度进行测量的整个过程进行分析与总结，希望能给读者带来一些启发。

一、圆环导轨平面度测量的基本原理

这里我们的测量方法主要建立在电子水平仪基础上，按水平仪测量方向将测量方法分为两种类型，切向测量法和径向测量法。

1.切向测量法的基本原理

切向测量法顾名思义是用水平仪对圆环导轨切向的水平倾角进行测量，从而得出圆环导轨的平面度。与直线导轨不同，圆环导轨测量所得到的数据做出的曲线不是一条直线，而是一条规律变化的曲线。

设想有一理想的标准圆导轨，它和物理水平面存在一微小的安装倾角，如图1所示。

图中圆环导轨面与水平面间夹角为α，D为该圆环导轨的最高点，A点为水平仪测量位置，A′、D′分别为它们在水平面的投影。∠OAB=90°可以得到

图1

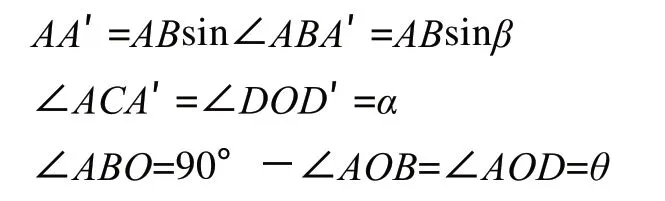
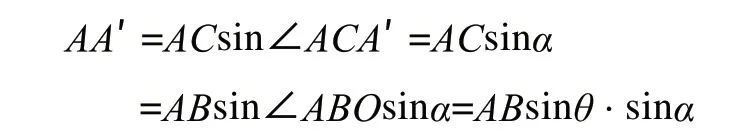
由上式可得

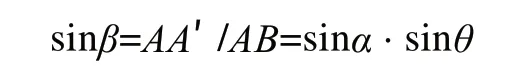
由于圆环导轨面与水平面间α夹角为非常小，β也就非常微小，所以

tanβ即为水平仪测量切向的读数，sinα为一常数，由式（1）我们可以知道水平仪的读数随着其测量点的相位角呈正弦函数变化。于是我们可以通过计算得到圆环导轨上各点的切向斜率，与测量数据进行比较分析，我们即可得出每点偏差，从而测得圆环导轨的平面度。

2.径向测量法

径向测量法即是通过测量圆环导轨上各点到圆环中心方向上的倾斜角得到的数据来计算各点的偏差，从而达到测量平面度的目的。但是实际测量中因为随着半径的增大，使得测量的精度成倍的减少，所以这个方法测量的精度相对切向测量法要低得多。

二、数据的测量与处理方法

在上述两种测量方法中，切向测量法不仅测量精度较高，而且所需测量工装比较简易，操作较为方便，因此我们选择切向测量法作为本次测量的主要手段。下面来介绍切向测量法如何测量数据并进行处理。

1.测量方法

测量前我们需要将圆环导轨面调水平，保证其与物理水平面只有一个微小的夹角。将水平仪调零，保证其读数精确可靠。

图2

将圆周均分为n等分，如图2所示，从任意位置A点开始将水平仪沿圆周切向按逆时针（或顺时针）方向依次首尾相连放置进行连续测量读数，并记录数据。测量过程中，水平仪不可调头，同时保证导轨面洁净。

2.数据处理方法

相对较为简易的测量步骤，测量数据的处理分析则显得复杂得多，它也是整个测量过程中的关键部分。由于水平仪测得的是每一等分部分沿圆周切向的倾角，即使我们得到各点测量数据与理论值的偏差我们也无法直观了解到各点凸出或凹入了多少，所以我们需要通过叠加法将各等分点间的倾角变成各点的相对高度值。

由式（1）我们知道倾角读数

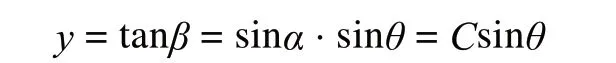
其中C=sinα为一常数，y呈正弦函数曲线。那么各点相对高度Y是不是也呈现为规律曲线呢？我们设起始相位角为的位置相对高度为0，则相位角为ψ的位置的相对高度Y为

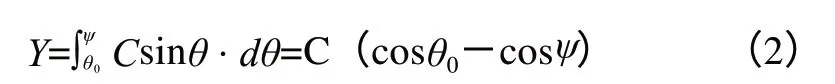
其中C和θ0均为常数，于是我们可以知道各点相对高度也是呈三角函数曲线的，将实际测得数据的累加值与理论计算值进行比较，得出各点的偏差作为依据对导轨面进行铲刮。

下面以LMV600转台底座上圆环导轨外圈的一组测量数据为例，来说明如何对数据进行分析处理。附表即是一组测量所得数据。

测量数据

（1）将测量得到的数据逐一进行累加处理，得到曲线如图3所示。

（2）连接曲线起点和终点，以连接两点所得到的斜线为x轴对累加处理的曲线进行坐标转换，即用累加曲线坐标减去斜线坐标得到新的曲线。如图4、5所示。

图3

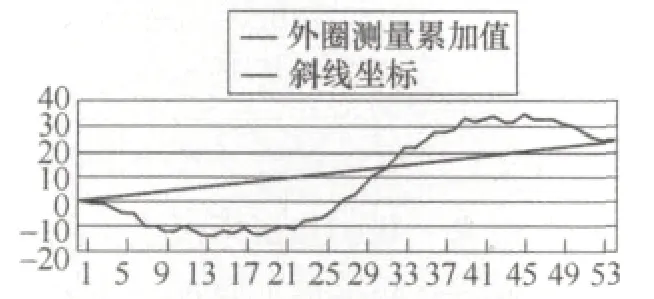
图4

图5

（3）将上一步得到的新曲线拟合成一条正弦函数曲线，这条正弦曲线的幅值为实测曲线最大值和最小值差值的一半，周期与实测曲线相同，我们移动该正弦函数曲线使其尽可能合理地靠拢实测曲线。如图6所示。

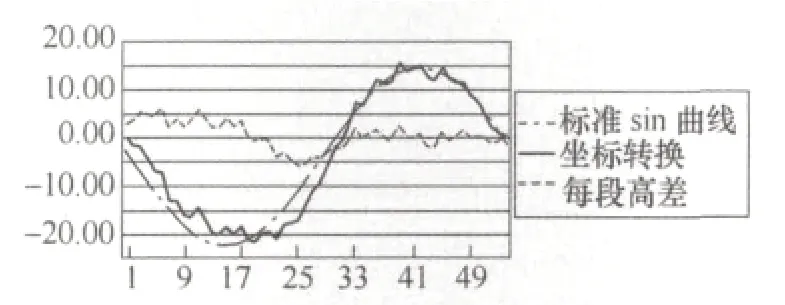
图6

图中两条曲线不重合处就是导轨面的平面度，两条曲线的差值即为各点相对理想圆环导轨面的偏差，实测曲线高出标准正弦曲线的部分为凸出的，而低于正弦曲线的部分则为凹下去的。

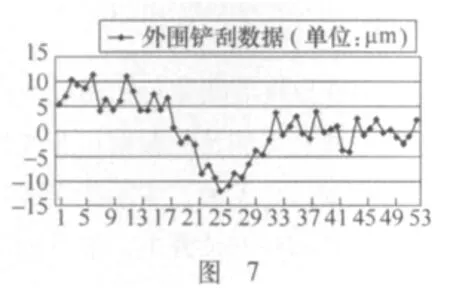
图7为各测量点数据与理想值的差值。从图中我们可以看到，最高凸出11μm、最低凹下去12μm，可以得到整个圆环导轨的平面度误差为11+12=23（μm）。

三、通过Matlab进行数据处理

上述数据处理都是通过Excel来完成，但是在最后进行拟合曲线时显然是存在一定问题，我们无法借助Excel很精确的将实测值拟合成正弦曲线。这里通过专业数据处理软件的来解决这一问题，利用Matlab软件可以很容易的完成任务。

1.Matlab数据处理程序

（1）创建一个目标函数

function diff=fit_sin（x，X，Y）

diff=x（1）+x（2）.*sin[X+x（3）]－Y；%创建目标函数供拟合用

（2）数据处理主程序 先将测量数据输入，然后由程序对数据按照步骤进行预处理，再将处理后的数据利用非线性回归拟合成目标函数，最后输出函数图像，程序实现如下：

DATA=input（'data='）；

n=input（'n='）； （输入测量数据）

s=sum（DATA）；

t=0:1:n；

Change=t*s/n； （斜线坐标）

Y（1）=0；

i=2；

while i<=n+1

Y（i）=sum（DATA（1:i-1））-Change（i）； （累加值坐标转换）

i=i+1；

end

X=0:2*pi/n:2*pi；

Y1=Y/10000；

X0=[1 1 1]'；

options=optimset（'Largescale'，'off'）；

x=lsqnonlin（@fit_sin，X0，[]，[]，options，X，Y1）； （拟合至目标函数）

Y_f i t=10000*x（1）+10000*x（2）.*s i n（X+x（3））；

Y_chan=Y-Y_fit；

Y_chan=Y_chan*200*0.01；（200为水平仪桥板长度，0.01为水平仪精度）

plot（X，Y，'r'，X，Y_fit，'b'，X，Y_chan，'k'）；（输出曲线图）

grid on

Y_chan

max（Y_chan）-min（Y_chan）（输出平面度误差）

2.结果分析与比较

将以上程序运行，输入表1中圆环导轨外圈的测量数据，便得到如图8曲线图，图中铲刮量就是我们需要的计算值。

图8

图中每点的铲刮量值为水平仪实测值与目标正弦函数的差值。由此图我们可以得知该圆环导轨凸出最高8.08μm，凹陷最低8.56μm，所以该圆环导轨平面度误差为16.64μm，精确拟合所得的结果竟比之前小了很多，利用软件进行精确计算的重要性可见一斑。

四、用Minitab 非线性回归的方法

从上述的分析过程来看，这是一个非线性回归的过程，我们同样也可以用Minitab 16.1 的这一功能来求精确解， 数据处理过程如下。

（1）新建一个工作表，如图9所示，在第一列C1中输入测量序号1～54（总的测量次数为54个点）。

图9

（2）在第二列C2中输入测量弧度， 公式为（测量序号－1）×360/54×PI（）/180。

（3）在第三列C3中输入实测值。

（4）在第四列C4中输入累加值（累加值在Minitab中不好处理，可以在Excel中处理后复制）。

（5）在第五列C5中输入坐标转换后的值，公式为累加值－SUM（实测值）/54×（测量序号－1） 。

（6）然后点击菜单栏→统计→非线性回归，输入公式“X1×S I N（C2+X2×P I（）/180）+X3”，如图10所示。

上述公式中：X1、X2、X3为回归变量，其中X1代表sin曲线的振幅，X2为sin曲线起始相位角，X3为sin曲线Y方向变化的常量。

（7）计算后自动求得残差1。

图10

（8）为计算实际的铲刮量，在C7列中输入如下的公式：残差1×200×0.01（其中200mm为水平仪测量桥板的长度，0.01mm为水平仪的精度）这样我们就可以得到非线性回归后的铲刮数值，如图11所示。

（9）如图12所示：我们可以看到非线性回归的拟合线图与计算后的回归方程，其结论也是精确的。

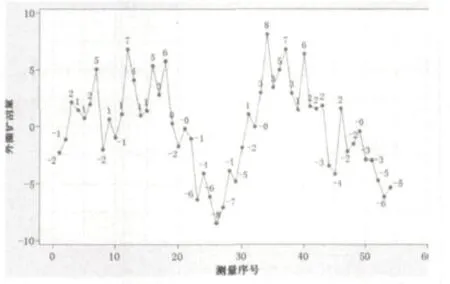
图11

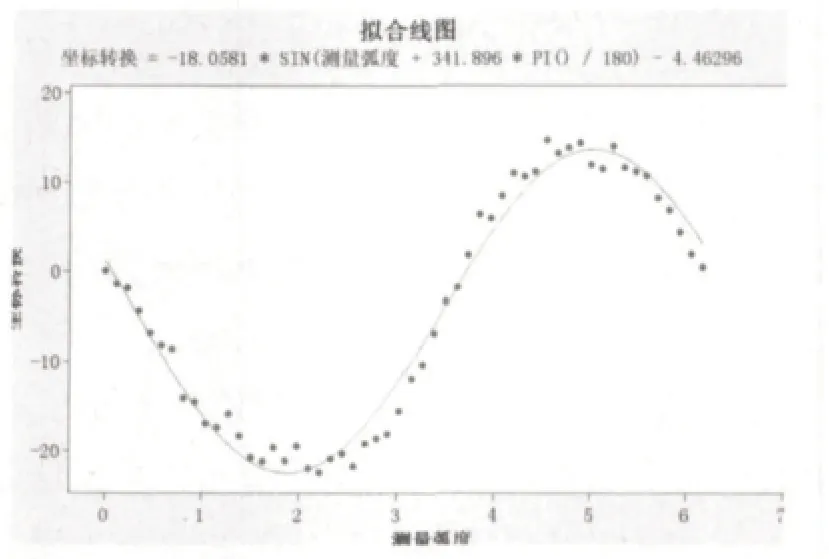
图12

五、结语

在大型平面圆导轨的测量与铲刮过程中，主要用切向测量法来测量，测量的数据用非线性回归的方法处理，与测量起点无关。实际操作过程中将每点计算值标在导轨相应的位置上，按点铲刮，可以大幅提高效率，以前手工铲刮需要20天的工作量，现在10天之内就能完成，精度也非常满意，极大地提高了生产效率。