卫星发射任务主动段实时弹道算法研究

胡亚男，甘友谊，王盛玺

(太原卫星发射中心，山西太原030027)

0 引言

在靶场卫星跟踪任务中，由于布站几何的限制，需利用脉冲雷达与3或4台高精度测速雷达联合解算实时弹道。传统的实时弹道计算方法有综合求速解析法和微分平滑法，这2种方法的优点是简单易行，但是由于对定位测元精度的依赖性很强，所以解算出的弹道精度不高。事后传统的数据融合方法——逐点多站最小二乘可以应用到实时弹道解算，但是目前的布站几何会导致在某个特定时间域出现计算发散的状况。“UKF”算法是在无迹变换(Unscented Transformation，UT)的基础上，借用卡尔曼线性滤波框架建立起来的，它利用非线性状态方程来估算状态向量的概率密度函数，其估计精确度对于任意非线性问题均可达到二阶以上［1］。采用上述不同方法解算实时弹道，分析评估弹道精度，对目前靶场实时弹道计算方法进行研究和评估。

1 实时弹道算法

1.1 综合求速

把脉冲雷达在测站坐标系中的观测量R、A、E转换成测站发射坐标系中的观测量R'、A'、E'后，根据几何关系，第tj时刻目标在发射坐标系中的位置参数Xj=［xj，yj，zj］T为:

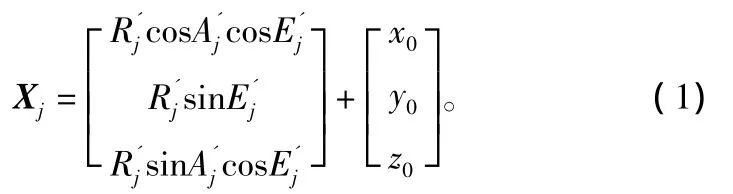
式中，x0、y0、z0为测站在发射坐标系中的站址坐标。

连续波多测速系统在tj时刻的观测方程为:

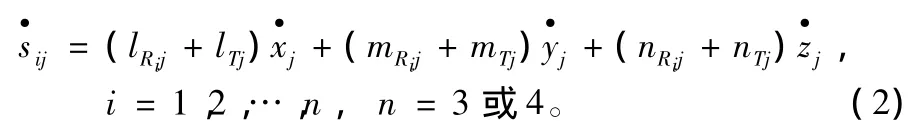
将式(2)的方程组写成矩阵形式为:

式中，

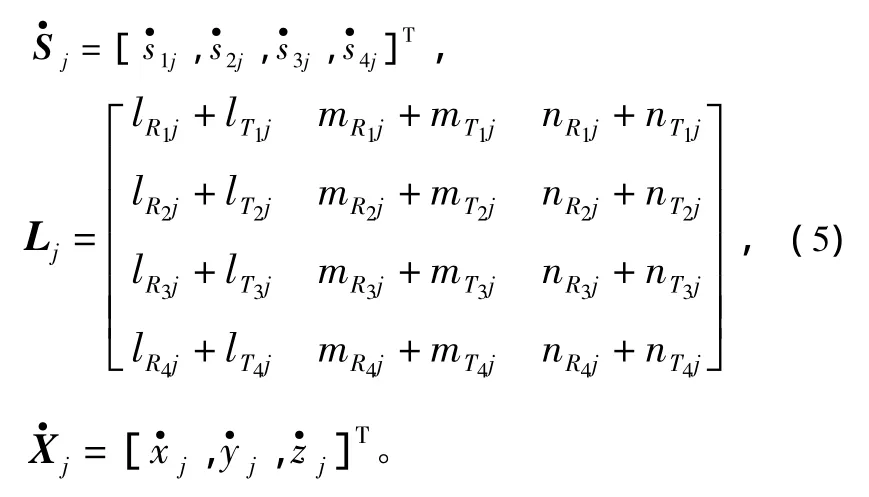
则tj时刻目标在发射坐标系中的速度参数为:

1.2 微分平滑

把脉冲雷达观测量转换到发射坐标系下，直接根据几何关系由式(1)得到目标在发射坐标系中的位置参数，然后使用最小二乘中心微分平滑公式对位置参数进行一阶微分，得到目标的速度参数为:

式中，h为步长;N为总平滑点数;n为中心平滑半点数;N=2n+1。

1.3 逐点多站最小二乘

第tj时刻脉冲雷达在发射坐标系的观测方程为:

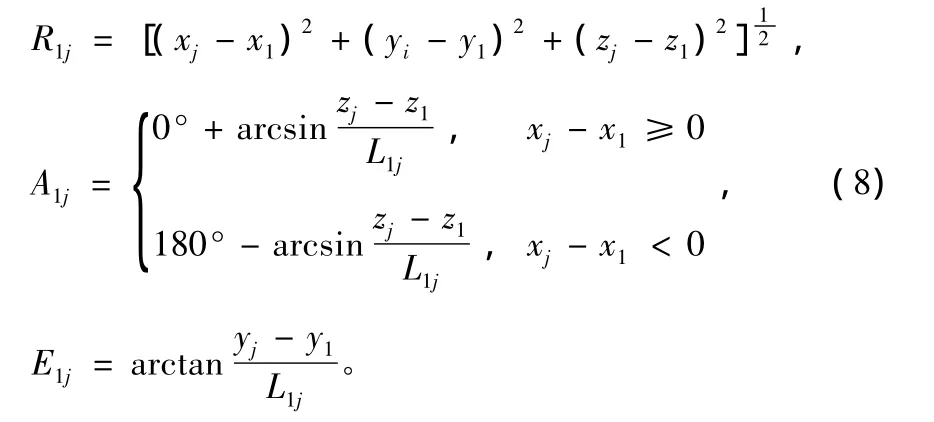
连续波测速雷达的观测方程为式(2)，由于式(8)和式(2)都是非线性方程，一般将该两式联立并泰勒展开成线性方程，设观测随机误差为ζj，则展开后的线性模型为:

式中，

而

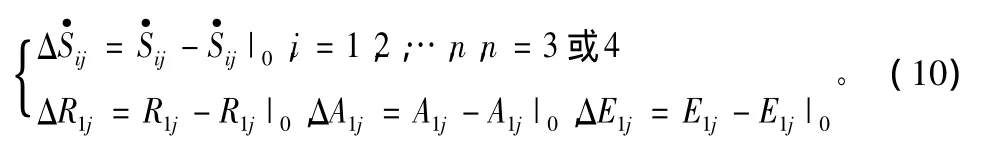
式中，(·)|0表示初始弹道参数代入对应方程得到的观测元素的初始值;Aj为各测量元素关于弹道参数的偏导数组成的雅可比矩阵，对应的值由初始弹道参数代入得到。

随机误差向量ζj满足利用高斯—马尔可夫估计得到tj时刻弹道参数增量ΔXj的最优线性无偏估计为:［2］

误差协方差阵为:

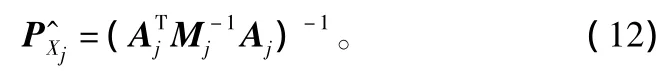
而tj时刻弹道参数Xj的估计值为:

通常需要迭代计算以提高弹道参数的解算精度。将第一次解算得到的弹道参数作为初始弹道参数，继续上述处理过程，直至解算的弹道参数增量很小为止。

1.4 UKF算法

Julier等人针对改进非线性滤波问题提出了基于UT的滤波思想，其相应算法称为无迹Kalman滤波(Unscented Kalman Filter，UKF)。该算法是在无迹变换(简称UT变换)的基础上，采用一种确定性抽样方法(Sigmadian的抽样方法)来计算均值和协方差。而UT变换的核心思想是:对概率密度函数的估计比非线性函数更容易［3－5］。理论证明UKF算法对于任意非线性问题均可达到二阶以上精度。

UKF的算法流程如下:

①σ点集及其权值的选取:在n维状态矢量集X={x1，x2，…，xn}中选取2n+1个σ点集及其相应权值。

②通过非线性函数f(·)传递σ点集:

③预测均值及协方差:

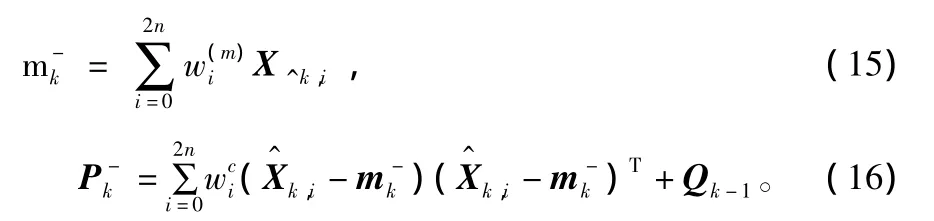
④将σ点集通过观测方程:

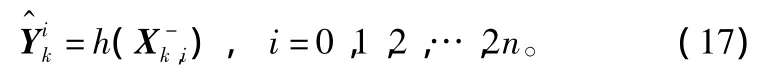
⑤计算:

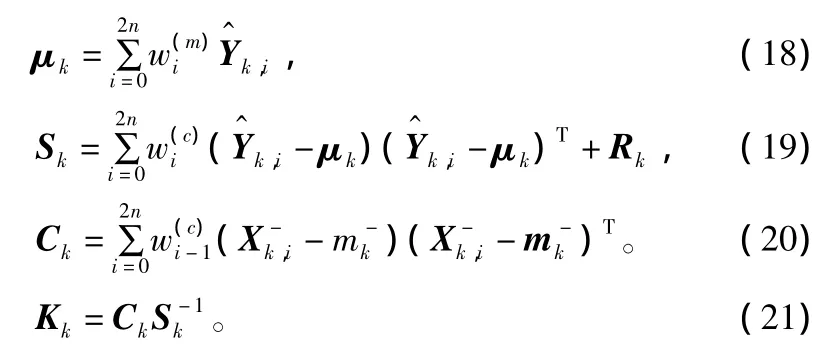
⑥更新状态均值mk和协方差Pk:

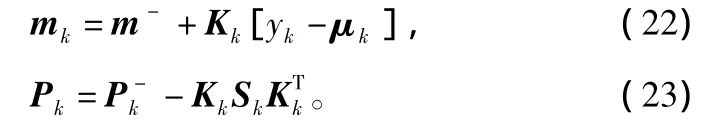
针对机动目标的 UKF算法，已有很多的应用［6～10］，仿真计算中采用的是一种基于“当前”统计模型的方法，文献［10］有较为详细的计算公式，这里不再赘述。

2 仿真结果分析

下面以某次卫星跟踪测量任务为例进行仿真计算，算例中使用的雷达测量数据均为事后修正数据。

从4种方法的计算过程和结果分析，可以说各有特点:

①传统的综合求速法计算简单，但对定位元的依赖性很大，也就是说对脉冲雷达实时测量数据的精度要求较高;② 微分平滑法完全依赖于定位测元，计算虽然最简单，但速度的计算没有与高精度测速元融合，因此速度精度很低;③ 由于跟踪几何的原因，逐点多站最小二乘法会出现雅克比矩阵局部奇异的现象，使计算结果发散;④ UKF算法不受跟踪几何影响，且计算结果精度较高，但对初值的选择有一定范围的要求，如果初值误差较大，也会出现发散的状况。

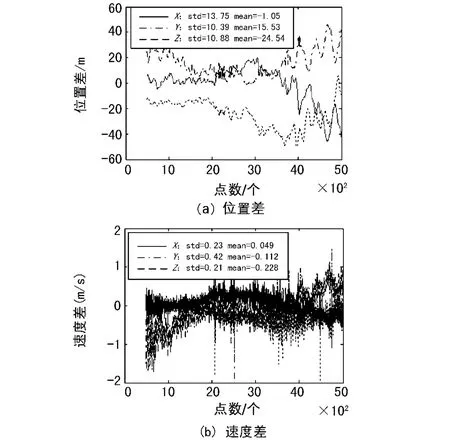
图1 综合求速法弹道比对结果

图2 微分平滑法弹道比对结果

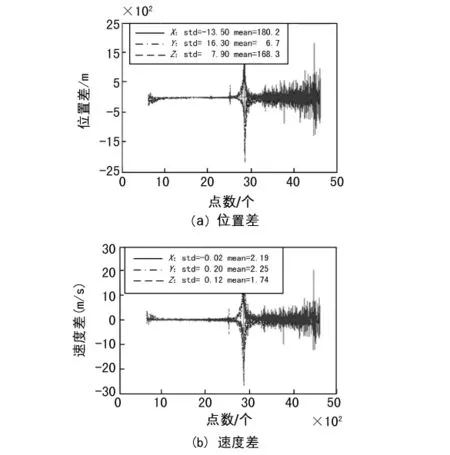
图3 逐点多站最小二乘法弹道比对结果

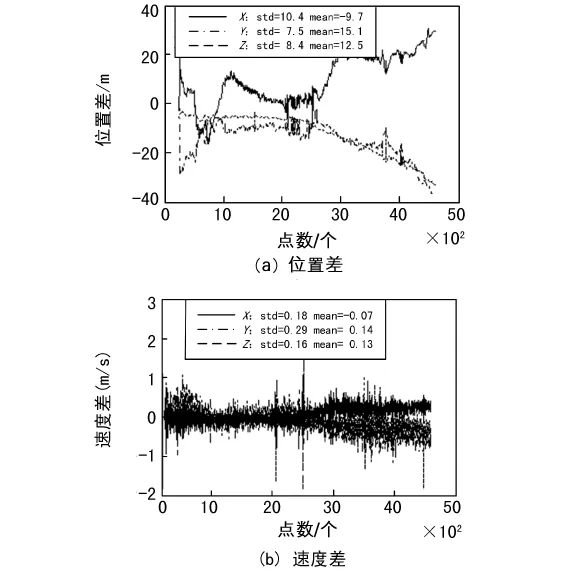
图4 UKF算法弹道比对结果

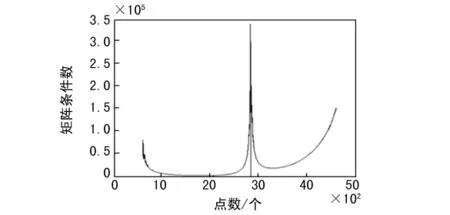
图5 最小二乘主法雅可比矩阵条件数

3 结束语

卫星发射任务时，采用UKF算法把脉冲雷达测元与高精度测速元融合，能够提高实时弹道解算的精度。但是需要对遴选初值的方法做进一步探讨;在出现极端情况(比如提供初值的设备出现异常)时，滤波器发散，如何再次获得满足要求的初值，如何有效地提高捕获初值的速度，都是下一步必须重点研究的内容。从另外一个角度考虑，如果能够提高脉冲雷达实时处理数据的精度，采用综合求速法计算实时弹道仍不失为一个简便而有效的方法。

［1］JULIER S J，UHIMANN J K，DURRANT H F.A New Approach for the Nonlinear Transformation of Means and Covariance in Filters and Estimators［J］.IEEE Trans on Automatic Control，2000，45(3):477 －482.

［2］刘利生.外测数据事后处理［M］.北京:国防工业出版社，2000:367－368.

［3］JULIER S J，UHIMANN J K.Unscented Filtering and Nonlinear Estimation［J］.Proceedings of the IEEE，2004，92(3):401－422.

［4］SINGER R A.Estimating Optimal Tracking Filter Performance for Manned Maneuvering Targets［J］.IEEE Trans on Aerospace and Electronic Systems，1970，5(4):473－483.

［5］JULIER S J，UHIMANN J K.Reduced Sigma Point Filters for the Propagation of Means and Covariance through Nonlinear Transformations［C］//Proceedings of the American Control Conference，2002:887 －892.

［6］彭 焱，金宏斌，徐 毓，等.一种改进的机动目标跟踪算法［J］.雷达与对抗，2007(4):54－56.

［7］唐 波，崔平远，陈阳舟.Unscented卡尔曼滤波在状态估计中的应用［J］.计算机仿真，2006(4):82－85.

［8］吴 玲，卢发兴，刘 忠.UKF算法及其在目标被动跟踪中的应用［J］.系统工程与电子技术，2005(1):49－51.

［9］王淑一，程 杨，杨 涤，等.ukf方法及其在方位跟踪问题中的应用［J］.飞行力学，2003(6):59－62.

［10］陈伟利，李 颢.基于“当前”模型的UKF滤波算法在目标跟踪与实时弹道估计中的应用［J］.导弹试验技术，2008(3):71－75.