三次Hermite参数曲线与曲面的扩展＊

2013-06-11李军成

计算机工程与科学 2013年1期

李军成，谢淳，杨炼

（湖南人文科技学院数学系，湖南娄底 417000）

1 引言

在计算机辅助几何设计中，往往需要调整曲线的形状或改变曲线的位置来满足曲线设计的要求。为解决这一问题，人们开始在曲线中引入形状参数，其大致通过两种方法实现。第一种方法是利用不同方法直接在传统的多项式曲线中引入形状参数。比如，Han［1］讨论了一种带形状参数的Bézier曲线与曲面的生成方法；吴荣军［2，3］分别给出了一类带形状参数的四次Bézier曲线和一类带形状参数的B样条曲线，并对这两种曲线的形状进行了分析；刘植［4］给出了一种带多个形状参数的广义Bézier曲线与曲面；范菊娴［5］讨论了另外一种带多个形状参数的Bézier曲线与曲面；刘华勇等［6］讨论了一类带两个形状参数的四次Ball曲线。第二种方法是通过改变多项式曲线的基空间，在非多项式函数（最为常见的是在带三角函数或双曲函数）的空间中构造带形状参数的曲线。比如，Han［7］给出了一类带两个形状参数的三次三角多项式Bézier曲线；Liu［8］研究了一种带形状参数的双曲多项式均匀B样条曲线与曲面；Han［9］提出了一种带参数的三次三角Bézier曲线并对其形状进行了分析；杨炼［10］研究了一类带形状参数的类四次三角Bézier曲线；严兰兰［11，12］讨论了几种带形状参数的三角样条曲线。这些带形状参数的曲线不仅具有原曲线的绝大部分性质，而且可通过调整形状参数的取值对曲线进行调节，从而使曲线更加灵活和实用。

作为一种常见的插值曲线与曲面，三次Hermite参数曲线与曲面又被称作Ferguson曲线与曲面［13］，在实际工程中具有广泛的应用。然而，当插值条件给定时，标准三次Hermite参数曲线与曲面的形状无法修改，不能满足一些实际工程的需要，因此讨论带形状参数的类三次Hermite参数曲线与曲面具有较高的应用价值。但遗憾的是，目前鲜有文献讨论直接在标准三次Hermite参数曲线与曲面中引入形状参数。为此，本文首先构造了一种带两个形状参数的四次Hermite基函数，然后生成了相应了四次Hermite参数曲线与曲面。该曲线与曲面是标准三次Hermite参数曲线与曲面的扩展，不仅具有标准三次Hermite参数曲线与曲面的性质，而且可通过修改形状参数的取值调节其形状，使得曲线与曲面具有更加优良的表现能力。

2 四次Hermite基函数

定义1 对t∈ ［0，1］，－1≤λ1，λ2≤1，称：

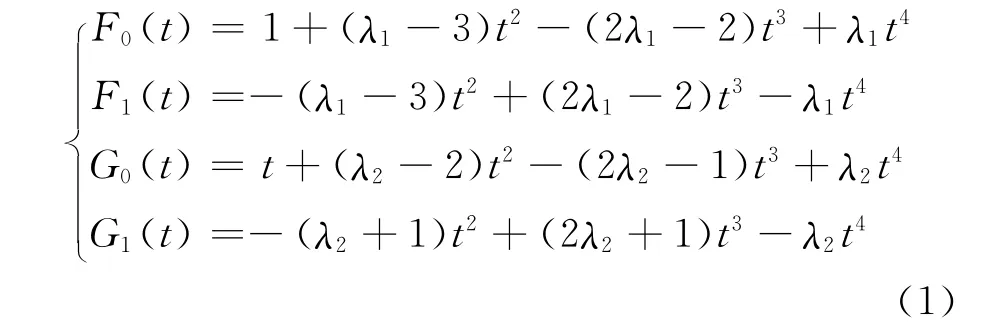
为带形状参数λ1与λ2的四次Hermite基函数。

四次Hermite基函数具有下列性质：

（1）退化性：由式（1）易知，当λ1＝λ2＝0时，四次Hermite基函数退化为标准的三次Hermite基函数。

（2）端点性：经简单计算可知，四次 Hermite基函数满足：

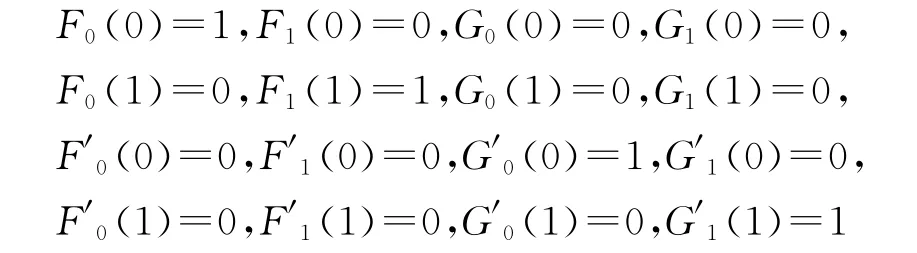
且F0（t）＋F1（t）＝1，G0（t）＝－G1（1－t）。

上述结论表明，四次Hermite基函数与标准三次Hermite基函数具有完全相同的性质，因此四次Hermite基函数是标准三次Hermite基函数的一种扩展。图1给出了四次Hermite基函数的图形，其中，长虚线部分对应λ1＝－1与λ2＝1，实线部分对应λ1＝λ2＝0（即为标准的三次Hermite基函数），短虚线部分对应λ1＝1与λ2＝－1。

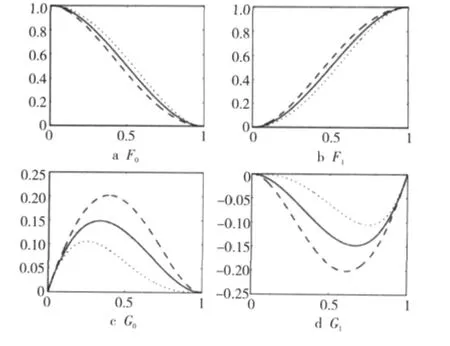
Figure 1 Quartic hermite basis functions图1 四次Hermite基函数

（3）对形状参数的单调性：固定变量t，对Fi（t）与Gi（t）（i＝0，1）分别求关于λ1与λ2的导数，分别记为DF0、DF1、DG0和DG1，则有DF0＝DG0＝t2（1－t）2≥0，DF1＝DG1＝－t2（1－t）2≤0，即F0（t）与G0（t）分别关于λ1与λ2单调递增，F1（t）与G1（t）分别关于λ1与λ2单调递减。

3 四次Hermite参数曲线

3.1 四次Hermite曲线段的定义及性质

定义2 对0≤t≤1，给定首、末端点Pi及其切矢P′i（i＝0，1），称：

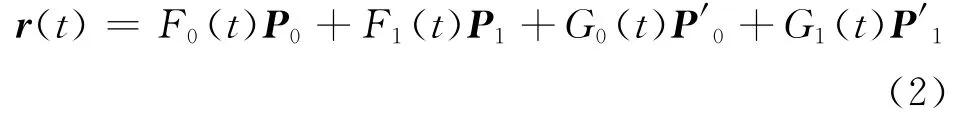
为带形状参数λ1与λ2的四次Hermite曲线段，其中Fj（t）与Gj（t）（j＝0，1）为式（1）定义的四次Hermite基函数。

由式（2）经简单计算有r（0）＝P0，r（1）＝P1，r′（0）＝P′0，r′（1）＝P′1，即表明四次 Hermite曲线段与标准三次Hermite参数曲线段具有完全相同的插值性，即插值于首、末端点Pi及其切矢P′i（i＝0，1）。特别地，当λ1＝λ2＝0时，四次Hermite曲线段退化为标准的三次Hermite参数曲线段。因此，四次Hermite曲线段是标准三次Hermite曲线段的一种扩展。

在给定插值条件时，标准三次Hermite参数曲线段的形状无法修改，但由于四次Hermite曲线段带有形状参数λ1与λ2，因此当给定插值条件时，四次Hermite曲线段的形状可通过改变形状参数λ1与λ2的取值进行调节。

例1 给定首、末端点及其切矢分别取P0＝（0，0），P1＝（2，0），P′0＝（1，3），P′1＝（1，－3），当形状参数取不同值时对应的四次Hermite曲线段如图2所示，其中，长虚线对应λ1＝－1与λ2＝1，实线对应λ1＝λ2＝0（即为标准三次Hermite曲线段），短虚线对应λ1＝1与λ2＝－1。

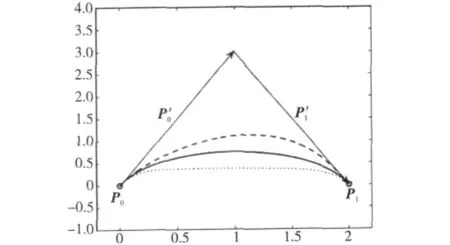
Figure 2 Quartic Hermite curves with different shape parameters图2 形状参数取不同值时的四次Hermite曲线段

3.2 四次Hermite曲线段的Bézier表达式

在适当条件下，标准三次Hermite参数曲线段可转化为三次Bézier曲线段。下面讨论四次Hermite曲线段与四次Bézier曲线段之间的转化关系。

一般地，一段四次Bézier曲线的矩阵表达式为［13］：

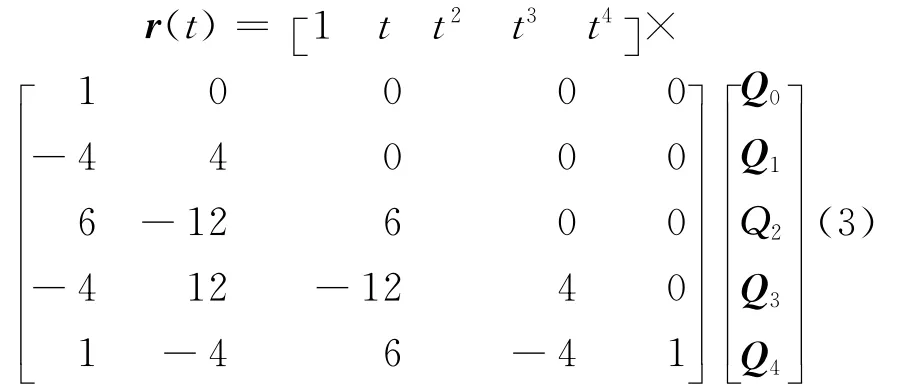
其中，Qi（i＝0，1，2，3，4）为控制顶点。

由式（2）与式（3）可知，四次 Hermite曲线段可表示成四次Bézier曲线段的形式，其中四次Bézier曲线段的控制顶点取为：

图3给出了当形状参数λ1与λ2取不同值时四次Hermite曲线段与四次Bézier曲线段的几何关系，其中，虚线部分对应λ1＝λ2＝0时四次Bézier曲线段的控制多边形，实线部分对应λ1＝－0.5与λ2＝0.5时四次Bézier曲线段的控制多边形。

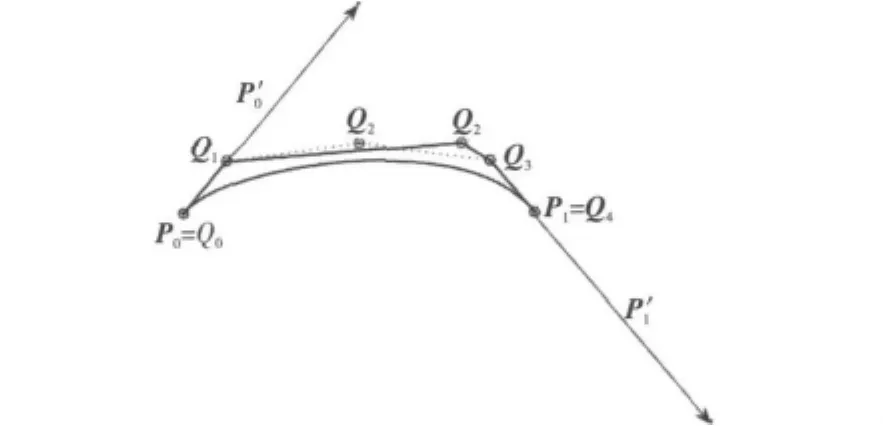
Figure 3 Geometric relationship between quartic hermite curve and quartic Bézier curve图3 四次Hermite曲线与四次Bézier曲线段的几何关系

3.3 整条四次Hermite曲线及其调节

若给定一列端点Pi及其切矢P′i（i＝0，1，2，…，n），则可由式（2）逐段构造出整条四次 Hermite曲线，其表达式可表示为：

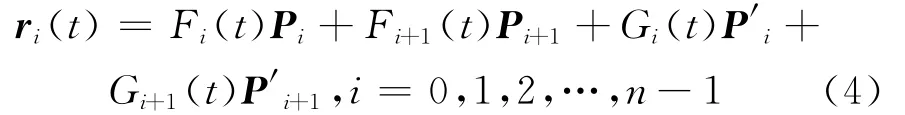
其中，Fi（t）、Fi＋1（t）、Gi（t）与Gi＋1（t）为按式（1）定义的四次Hermite基函数，其形状参数为λi1与λi2（i＝0，1，2，…，n－1）。

由式（4）不难验证：

上式表明，整条四次Hermite曲线插值于各端点Pi及其切矢P′i（i＝0，1，2，…，n），且满足C1连续。

当插值条件给定时，整条标准三次Hermite参数曲线的形状是无法改变的，但整条四次Hermite曲线的形状却可通过改变形状参数λi1与λi2的取值对进行局部或整体调节，且整体曲线仍满足C1连续，这样给设计人员进行交互设计带来了方便。

例2 若给定端点及其切矢分别为P0＝（0，0），P1＝（1，0），P2＝（2，0），P3＝（3，0），P4＝（4，0），P′0＝（0，1），P′1＝（0，－1），P′2＝（0，1），P′3＝（0，－1），P′4＝（0，1），则可绘制出由四段四次Hermite曲线段拼接而成的整条C1连续开曲线，并可通过修改参数λi1与λi2（i＝0，1，2，3，4）的取值实现对整条开曲线的局部或整体调节。图4为形状参数λ21对开曲线进行局部调节的情形，这里取λi1＝λj2＝1（i＝0，1，3；j＝0，1，2，3），其中，长虚线对应λ21＝－1，实线对应λ21＝0，短虚线对应λ21＝1。图5为形状参数对开曲线进行整体调节的情形，这里取λi1＝λ1，λi2＝λ2（i＝0，1，2，3），其中，长虚线对应λ1＝－0.5与λ2＝0.5，实线对应λ1＝λ2＝0（即为标准三次Hermite曲线），短虚线对应λ1＝0.5与λ2＝－0.5。

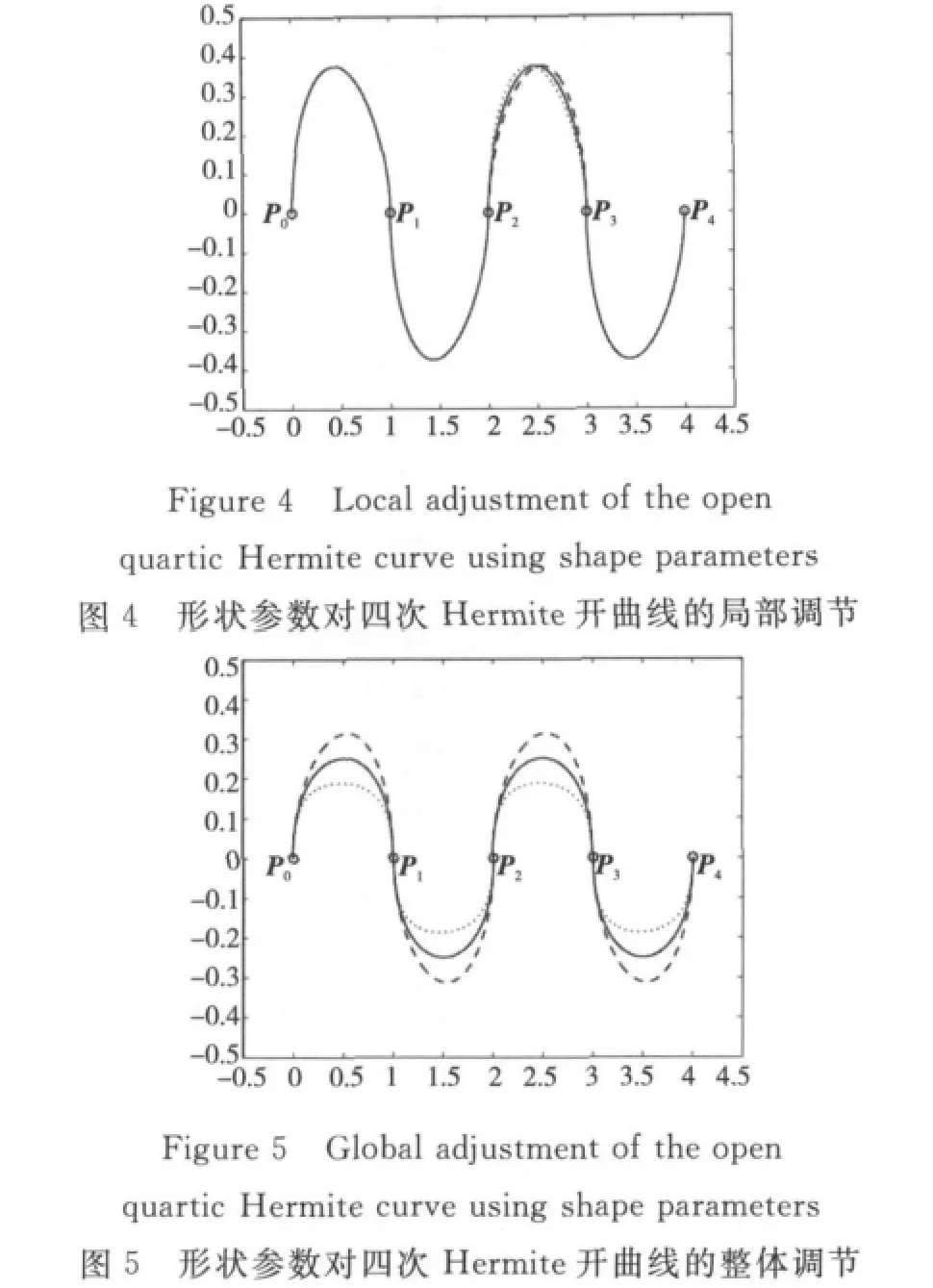
例3 若给定型值点及其切矢分别为P0＝P4＝（－1，0），P1＝（0，1），P2＝（1，0），P3＝（0，－1），P′0＝P′4＝（0，1），P′1＝（1，0），P′2＝（0，－1），P′3＝（－1，0），则可绘制出由四段四次Hermite曲线段拼接而成的整条C1连续闭曲线，并可通过修改参数λi1与λi2（i＝0，1，2，3，4）的取值对整条闭曲线进行局部或整体调节。图6为形状参数λ22对整条闭曲线进行局部调节的情形，这里取λi1＝λj2＝1（i＝0，1，2，3；j＝0，1，3），其中，长虚线对应λ22＝－1，实线对应λ22＝0，短虚线对应λ22＝1。图7为形状参数对闭曲线进行整体调节的情形，这里取λi1＝λ1，λi2＝λ2（i＝0，1，2，3），其中，长虚线对应λ1＝－0.5与λ2＝0.5，实线对应λ1＝λ2＝0（即为标准三次Hermite曲线），短虚线对应λ1＝0.5与λ2＝－0.5。

4 曲面的定义及性质

类似于曲线，可定义带形状参数的分片四次Hermite曲面。四次Hermite曲面与四次Hermite曲线有相似的性质。

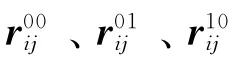
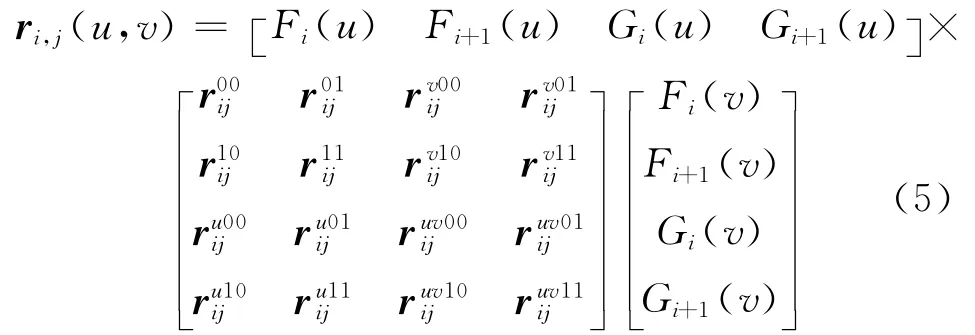
为带形状参数的四次Hermite曲面，其中，Fi（t）、Fi＋1（t）、Gi（t）与Gi＋1（t）（t＝u，v）为按式（1）定义的四次Hermite基函数，且u向的形状参数为αi1与αi2，v向的形状参数为βi1与βi2。

由式（5）不难验证：

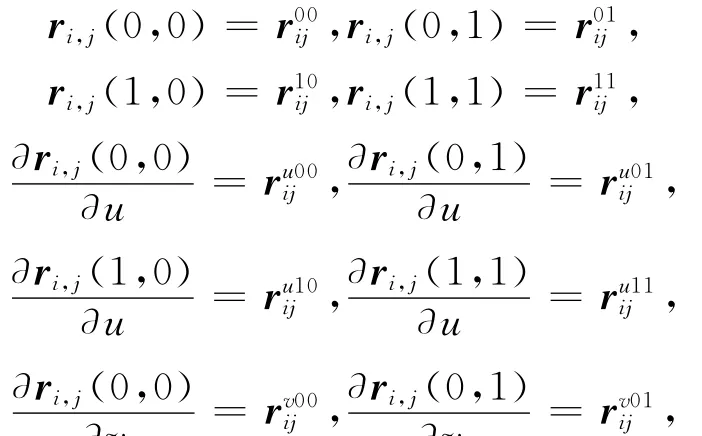
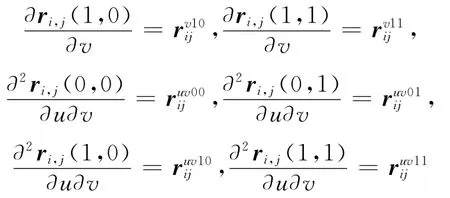
上述结论表明，四次Hermite曲面与标准三次Hermite参数曲面具有完全相同的插值性及C1连续性。特别地，当形状参数取αi1＝αi2＝βi1＝βi2＝0时，四次Hermite曲面即退化为标准的三次Hermite参数曲面。因此，四次Hermite曲面是标准三次Hermite曲面的一种扩展。

当给定插值条件时，标准三次Hermite参数曲面的形状无法修改，但由于带有形状参数，在给定插值条件时，四次Hermite曲面的形状可通过修改参数的取值进行局部或整体调节，且曲面片之间仍能保证C1连续性。

例4 若插值条件取为：

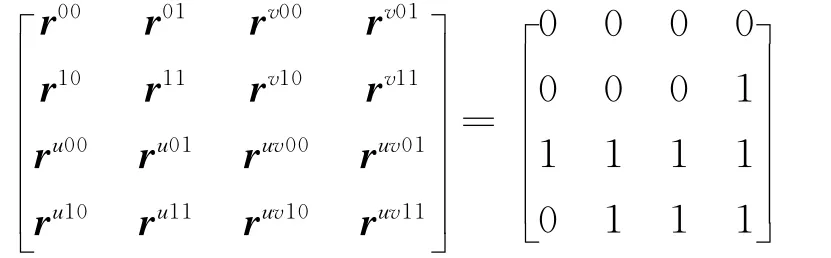
当形状参数α1、α2、β1与β2取不同值时所得到的一片四次Hermite参数曲面如图8所示。

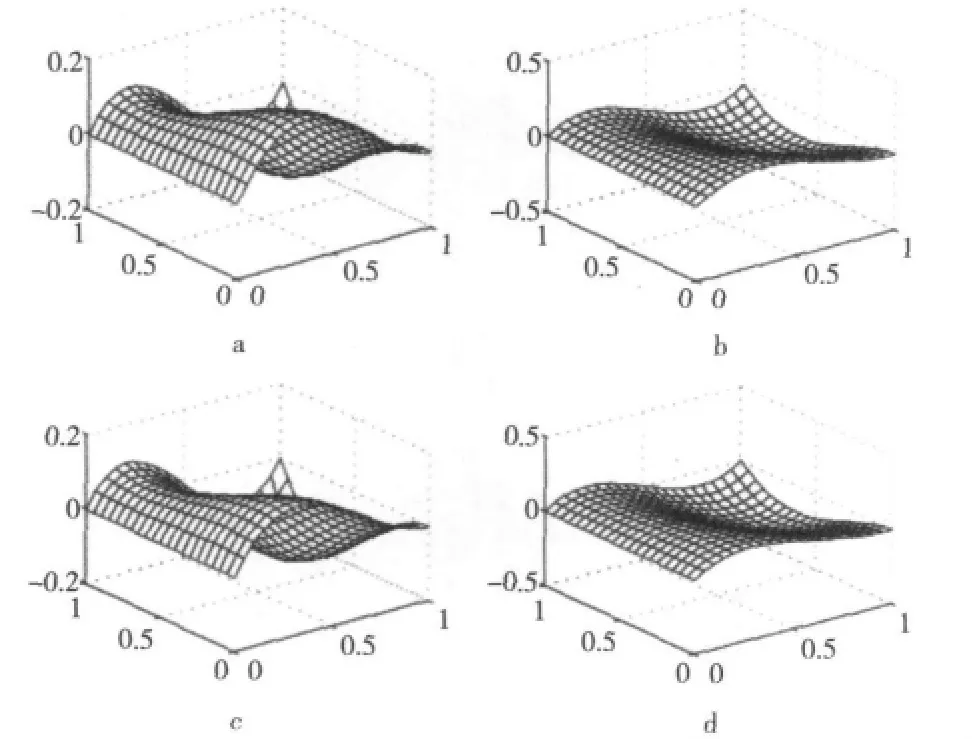
Figure 8 Quartic Hermite surfaces with different shape parameters图8 参数取不同值时的四次Hermite曲面片

图8a～图8d分别对应的参数为：（1）α1＝－0.5，α2＝0.5，β1＝0.5，β2＝－0.5；（2）α1＝－0.5，α2＝0，β1＝0，β2＝0.5；（3）α1＝α2＝β1＝β2＝0（即为标准三次Hermite参数曲面片）；（4）α1＝0.5，α2＝－0.5，β1＝－0.5，β2＝0.5。由图8可知，当形状参数取不同值时，可使得四次Hermite曲面片的内部呈不同程度的起伏变化。

5 结束语

为克服传统三次Hermite参数曲线与曲面的不足，本文讨论了一种带形状参数的四次Hermite曲线与曲面，该曲线与曲面是标准三次Hermite参数曲线与曲面的扩展，不仅与标准三次Hermite参数曲线与曲面具有相同的性质，而且可以通过修改形状参数的取值对曲线与曲面的形状进行局部或整体调节，为插值曲线与曲面的构造提供了一种有效的方法。如何通过选取形状参数使得四次Hermite曲线与曲面满足C2连续，将是下一步要研究的问题。

［1］Han X A，Ma Y C，Huang X L.A novel generalization of Bézier curve and surface［J］.Journal of Computational and Applied Mathematics，2008，217（1）：180－193.

［2］Wu Rong－jun，Peng Guo－hua，Luo Wei－min，et al.Shape analysis of quartic Bézier curve with shape parameter［J］.Journal of Computer－Aided Design ＆ Computer Graphics，2009，21（6）：725－729.（in Chinese）

［3］Wu Rong－jun，Peng Guo－hua，Luo Wei－min.Shape analysis of a class of b－spline curve with shape parameters［J］.Mathematica Numerica Sinica，2010，32（4）：349－360.（in Chinese）

［4］Liu Zhi，Chen Xiao－yan，Jiang Ping.A class of generalized Bézier curves and surfaces with multiple shape parameters［J］.Journal of Computer－Aided Design ＆Computer Graphics，2010，22（5）：838－844.（in Chinese）

［5］Fan Ju－xian，Tan Jie－qing.Bézier curves and surfaces with multiple shape parameters［J］.Journal of Hefei University of Technology：Natural Science，2011，34（1）：149－152.（in Chinese）

［6］Liu Hua－yong，Li Lu，Zhang Da－ming.Quadratic ball curve with multiple shape parameters［J］.Journal of Shandong U－niversity：Engineering Science，2011，41（2）：23－28.（in Chinese）

［7］Han X A，Ma Y C，Huang X L.The cubic trigonometric Bézier curve with two shape parameters［J］.Applied Mathematics Letters，2009，22（2）：226－231.

［8］Liu X M，Xu W X，Guan Y，et al.Hyperbolic polynomial uniform B－spline curves and surfaces with shape parameter［J］.Graphical Models，2010，72（1）：1－6.

［9］Han X A，Huang X L，Ma Y C.Shape analysis of cubic trigonometric Bézier curves with a shape parameter［J］.Applied Mathematics and Computation，2010，25（3）：361－366.

［10］Yang Lian，Li Jun－cheng.A class of quasi－quartic trigonometric polynomial Bézier curves with a shape parameter［J］.Computer Engineering ＆ Science，2011，33（3）：77－81.（in Chinese）

［11］Yan Lan－lan，Liang Jiong－feng.A trigonometric spline curve with shape parameters［J］.Computer Engineering ＆ Science，2011，33（5）：69－73.（in Chinese）

［12］Yan Lan－lan，Liang Jiong－feng.Two kinds of curves with shape parameters［J］.Computer Engineering ＆ Science，2011，33（6）：57－62.（in Chinese）

［13］Zhu Xin－xiong.Technology for free curves and surfaces modeling［M］.Beijing：Science Press，2000.（in Chinese）

附中文参考文献：

［2］吴荣军，彭国华，罗卫民，等.四次带参Bézier曲线的形状分析［J］.计算机辅助设计与图形学学报，2009，21（6）：725－729.

［3］吴荣军，彭国华，罗卫民.一类带参B样条曲线的形状分析［J］.计算数学，2010，32（4）：349－360.

［4］刘植，陈晓彦，江平.带多形状参数的广义Bézier曲线曲面［J］.计算机辅助设计与图形学学报，2010，22（5）：838－844.

［5］范菊娴，檀结庆.带多个形状参数的Bézier曲线和曲面［J］.合肥工业大学学报：自然科学版，2011，34（1）：149－152.

［6］刘华勇，李璐，张大明.带形状参数的四次Ball曲线［J］.山东大学学报：工学版，2011，41（2）：23－28.

［10］杨炼，李军成.一类带形状参数的类四次三角Bézier曲线［J］.计算机工程与科学，2011，33（3）：77－81.

［11］严兰兰，梁炯丰.一种带形状参数的三角样条曲线［J］.计算机工程与科学，2011，33（5）：69－73.

［12］严兰兰，梁炯丰.两种带形状参数的曲线［J］.计算机工程与科学，2011，33（6）：57－62.

［13］朱心雄.自由曲线曲面造型技术［M］.北京：科学出版社，2000.

LI Jun－cheng，born in 1982，PhD candidate，lecturer，CCF member（E200012001M），his research interests include computer aided geometric design，geometric modeling and image processing.