一类分数阶超混沌系统的同步及其应用＊

谭 文，蒋逢灵，王耀南，刘贤群，伍 丰

（1.湖南科技大学信息与电气工程学院，湖南 湘潭411201；2.湖南大学电气与信息工程学院，湖南 长沙410082）

1 引言

虽然分数阶微积分已有三百多年的研究历史，但是它在物理和工程方面的应用还只是近年来关注的热点［1］。最近，越来越多的学者开始研究分数阶混沌系统的控制及其动力学行为，发现混沌现象和超混沌现象同样存在于分数阶混沌系统中［2，3］。分数阶系统更具有普遍性和更大的密钥空间，并且分数阶超混沌系统具有比低维混沌系统更加复杂的动力学行为［4］。自从Pecora等［5］开创性地提出混沌同步的概念和方法后，混沌系统的控制与同步激起了广大科研工作者的兴趣。随着越来越多的学者对混沌理论的深入研究，提出了各种有关混沌控制和混沌同步的方法［6，7］。分数阶超混沌系统的混沌同步主要是基于分数阶稳定性理论，通常是设计控制器，使响应系统与驱动系统实现同步。这种控制方法虽然取得了一定的效果，但是在响应系统添加控制器，一般需设计三个以上控制器［8～10］。尽管这些方法可以实现系统之间的同步，但同时也导致系统结构更复杂，并在一定程度上影响实际工程的应用。

近几年，分数阶混沌系统在保密通信和过程控制方面的潜在应用，引起了国内外众多学者的关注。然而，据现有文献分析，很多研究者只是关注简单周期信号在保密通信中的应用［11，12］，而复杂非周期信号的应用相对较少。然而，实际传送的信号大多是不规则的，所以对复杂非周期信号在保密通信中的应用研究具有十分重要的意义。

本文提出了一类分数阶超混沌系统同步控制器设计方法，只需要在响应系统中设计两个控制器，便能实现两个分数阶Chen超混沌系统的同步，简化了控制设计过程。最后，利用混沌掩盖技术，将该方案应用到保密通信中。

2 分数阶微分及其逼近

分数阶微分的定义有很多种［1］，这里采用经典的Caputo［1］定义：

其中，n是不小于α的第一个整数，Jβ是β阶Riemann-Liouville积分算子，其表达式为：

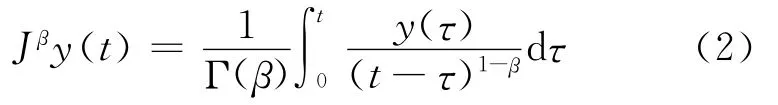
这里，Γ（·）是伽马函数，0＜β≤1。

假设分数阶混沌系统为：

其中，X1∈ Rn×1，F（X1）＝ （f（X1），f（X2），…，f（Xn））T，并且0＜q≤1。令系统（3）等于零，即：

相应的响应系统为：

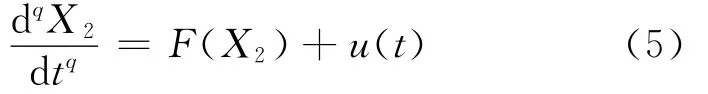
其中，X2∈Rn×1，u（t）是控制函数。假设系统（3）与系统（5）之间的误差为e（t）＝X1（t）－X2（t），因此得到分数阶误差系统为：

文献［13］分析了分数阶系统稳定的充要条件。

因此，两个分数阶混沌系统之间的同步问题，可以转化为分析分数阶误差系统的稳定性问题。在讨论此方法之前，首先给出分数阶稳定性的一个引理。

引理1［13］系统（3）是渐近稳定的，当且仅当对于系统（3）的雅克比矩阵的任意特征值λi（i＝

文献［10，14］给出了分数阶混沌系统阶次为0＜q≤1的稳定性区域坐标分布图。显而易见，分数阶混沌系统较之相对应的整数阶X·1＝F（X1）混沌系统的稳定区域范围宽。于是，我们得到一个关于分数阶系统稳定性的推论。

推论1 当整数阶混沌系统是稳定的，那么它相对应的分数阶混沌系统必定是渐近稳定的。

3 分数阶Chen超混沌系统的描述

分数阶Chen超混沌系统表示为：

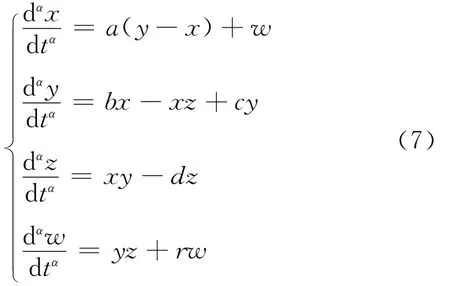
其中α是系统（7）的阶数（0＜α＜1）。图1所示为分数阶超混沌吸引子相图。

Figure 1 Attractor system of（7）with a＝35，b＝7，c＝12，d＝3and r＝0.5，α＝0.96图1 系统（7）的超混沌吸引子（a＝35，b＝7，c＝12，d＝3和r＝0.5，α＝0.96）

4 分数阶Chen超混沌系统之间的同步

在本节中，我们研究分数阶Chen超混沌系统之间的同步。以分数阶Chen超混沌系统（7）为驱动系统，则相应的响应系统为：

由系统（8）和系统（7）可得到误差动态系统：

根据系统（9）设计控制器u1和u2，定义控制函数为：

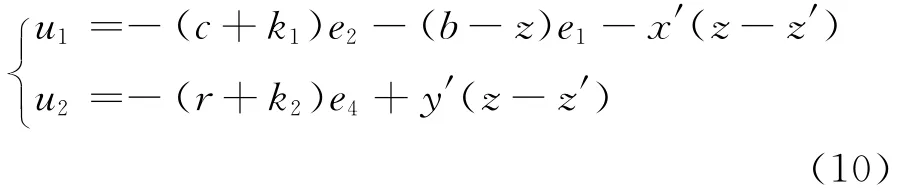
由系统（9）和式（10）可得：

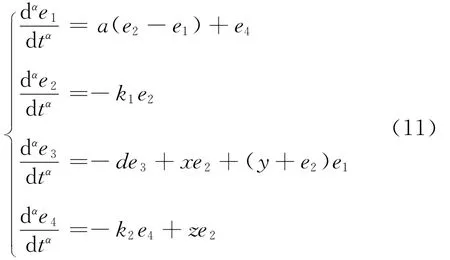
其对应整数阶系统进行线性化，求得整数阶系统的雅克比矩阵为：

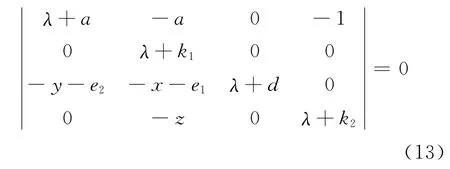
将式（13）变换为：

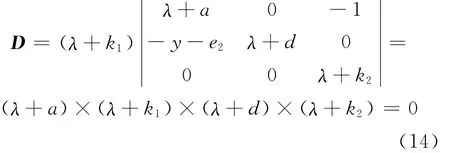
显而易见，由式（14）可求出整数阶系统的特征根为－a，－k1，－d，－k2。当k1和k2取正常数时，矩阵A的特征根均小于零，所以整数阶混沌系统是稳定的。由推论1可知，其相对应的分数阶系统式（11）是渐近稳定的。所以，当t→ ∞ 时，lime1（t）、lime2（t）、lime3（t）和 lime4（t）均 趋 于零，即两个分数阶Chen超混沌系统之间实现了同步。为了验证理论分析的正确性，取系统参数a＝35，b＝7，c＝12，d＝3和r＝0.5，k1＝15，k2＝20，α＝0.96；驱动系统（7）的初始值为x（0）＝10，y（0）＝10，z（0）＝10，w（0）＝10；相应的响应系统（8）的初始值为x′（0）＝－10，y′（0）＝－10，z′（0）＝－10，w′（0）＝－10。从图2中我们可以发现，大约在2.2s后，误差e1（t）、e2（t）、e3（t）和e4（t）均趋于零，因此系统（8）与系统（7）实现了同步。数值仿真结果证实了理论分析的正确性。

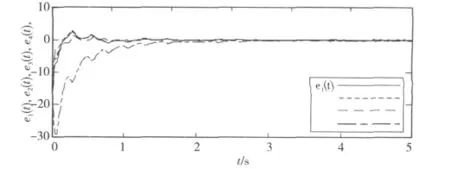
Figure 2 Synchronization of error curve with system （8）and system （7）图2 系统（8）与系统（7）的同步误差曲线

5 同步控制在保密通信中的应用

设x（t）是驱动系统的混沌状态变量，x′（t）是响应系统的混沌状态变量，S（t）是需要传送的有用信号，M（t）是混沌信号与有用信号的叠加信号，根据通信原理和混沌掩盖技术，有M（t）＝S（t）＋x（t），S0（t）是去掩盖后恢复的有用信号，那么去掩盖后，S0（t）＝M（t）－x′（t）。

为了增强方案的可行性，选取随机信号作为有用传送信号。经过混沌掩盖后的信号（如图4所示），与原发送信号完全不一样（如图3所示），便于信号的保密传送，从而达到了信号安全传送且不被破译的目的。经过同步信号x′（t）的去掩盖，在接受端经过1.2s（e1（t）趋于零）后，毫无失真地恢复了有用信号，即解调后的信号S0（t）再现了需要发射传输的信号S（t），从而可以实现保密通信的目的（如图5所示）。同时研究发现，即便采用其它复杂非周期信号，同样可以达到保密通信的目的。

6 结束语

本文提出了一类分数阶超混沌系统控制器的设计方法、实现了分数阶超混沌系统之间的同步，并且将该方案应用到保密通信中，达到了保密通信的目的。数值仿真结果验证了该方案的有效性和可行性。该方案不但可以应用在保密通信中，在信号传输和图像处理等其它领域也有潜在的应用价值，下一步将利用分数阶混沌同步技术研究高频数字信号传输应用问题。

［1］ Podlubny I.Fractional differential equations［M］.New York：Academic Press，1999.

［2］ Li C，Chen G.Chaos and hyperchaos in the fractional order Rossler equations［J］.Physica A，2004，341（4）：55-61.

［3］ Wu X，Lu Y.Generalized projective synchronization of the fractional-order Chen hyperchaotic system［J］.Nonlinear Dynamics，2009，57（1）：25-35.

［4］ Zhang H G，Zhao Y，Yu W，et al.A unified approach to fuzzy modelling and robust synchronization of different hyperchaotic systems［J］.Chinese Physics B，2008，17（11）：4056-4066.

［5］ Pecora L M，Carroll T L.Synchronization in chaotic systems［J］.Physical Review Letters，1990，64（8）：821-824.

［6］ Erjaee G H，Momani S.Phase synchronization in fractional differential chaotic systems［J］.Physics Letters A，2008，372（14）：2350-2354.

［7］ Ma Tie-dong，Zhang Hua-guang，Wang Zhi-liang.Impulsive synchronization for unified chaotic systems with channel time-delay and parameter uncertainty［J］.Acta Physica Sinica，2007，56（7）：3796-3802.（in Chinese）

［8］ Zhao Ling-dong，Hu Jian-bing，Liu Xu-hui.Adaptive tracking control and synchronization of fractional hyper-chaotic Lorenz system with unknown parameters［J］.Acta Physica Sinica，2010，59（4）：2305-2309.（in Chinese）

［9］ Liu Fu-cai，Li Jun-yi，Zang Xiu-feng.Anti-synchronization of different hyperchaotic systems based on adaptive active control and fractional sliding mode control［J］.Acta Physica Sinica，2011，60（3）：030504.（in Chinese）

［10］ Sun Ning，Zhang Hua-guang，Wang Zhi-liang.Fractional sliding mode surface controller for projective synchronization of fractional hyperchaotic systems［J］.Acta Physica Sinica，2011，60（5）：050511.（in Chinese）

［11］ Kiani-B A，Fallahi K，Pariz N，et al.A chaotic secure communication scheme using fractional chaotic systems based on an extended fractional Kalman filter［J］.Communications in Nonlinear Science and Numerical Simulation，2009，14（3）：863-879.

［12］ Deng Yang-song，Qin Kai-yu.Fractional order Liu-system synchronization and its application in multimedia security［C］∥Proc of Communicaiton，Circuits and Systems，2010：769-772.

［13］ Matignon D.Stability results of fractional differential equations with applications to control processing［M］.Lille，France：IMACS，IEEE-SMC，1996：963-968.

［14］ Hu Jian-bing，Han Yan，Zhao Ling-dong.Synchronizing fractional chaotic systems based on Lyapunov equation［J］.Acta Physica Sinica，2008，57（12）：7522-7526.（in Chinese）

附中文参考文献：

［7］ 马铁东，张化光，王智良.一类参数不确定统一混沌系统的脉冲滞后同步［J］.物理学报，2007，56（7）：17-23.

［8］ 赵灵冬，胡建兵，刘旭辉.参数未知的分数阶超混沌Lorenz系统的自适应追踪控制与同步［J］.物理学报，2010，59（4）：2305-2309.

［9］ 刘福才，李俊义，臧秀凤.基于自适应主动及滑模控制的分数阶超混沌系统异结构反同步［J］.物理学报，2011，60（3）：030504.

［10］ 孙宁，张化光，王智良.基于分数阶滑模面控制的分数阶超混沌系统的投影同步［J］.物理学报，2011，60（5）：050511.

［14］ 胡建兵，韩焱，赵灵冬.基于Lyapunov方程的分数阶混沌系统同步［J］.物理学报，2008，57（12）：7522-7526.